【编程开发】浅谈公开密钥加密技术
好吧,阮一峰大神比我写的好:http://www.ruanyifeng.com/blog/2013/07/rsa_algorithm_part_two.html
1.为什么要用公开密钥加密?
答:公开密钥加密技术解决了“密钥分发”的问题。
可以些许的参考下51CTO 的这篇文章 :http://book.51cto.com/art/200902/108049.htm
总之,密钥分发是件耗时耗力的事情--而这时几千年来对称密钥密码学都必须面对的一个难题。
那么,有没有什么技术能都让通信双方不依赖于密钥分配就可以安全的进行通信网来呢?---》公开密钥技术解决了这个难题。
2.公开密钥技术:
公有密钥技术依赖于两个不同的密钥,一个公有密钥和一个私有密钥。公有密钥用于加密信息,私有密钥用于解密它们。
下图是一种非对称加密技术:

实现原理:
Diffie–Hellman key exchange:

现在假设A和B分别是参与DH式密钥交换过程的两方,他们一开始会商议确定一个小质数(一般是2,3,5这样的小数字)和一个大质数(有300位以上)作为加密的原始信息。小质数和大质数都可以直接传输,不必担心交换过程中的不安全。需要明白的是,A和B各自都持有着自己的私钥(100多位的数),而且也永远不应该共享自己的私钥。不光是两人之间,也包括其他不相关的人都不应该拥有这两组私钥。网络中传输的是他们的私钥、小质数和大质数混合运算得到的结果。更确切来说,就是:
- A的结果 = (小质数A的密码)% 大质数
- B的结果 = (小质数B的密码)% 大质数
- (“%” 符号表示取模运算,即取得除法运算的余数)
所以A使用大质数和小质数加上自己的私钥运算,就会得出结果,而B做同样的计算,也能得到相同的结果。当他们接收到对方的运算结果时,他们可以由数学计算导出会话中所要传输的信息,也就是说:
A计算的是
- (B的结果Alice的密码)% 大质数
而Bob则计算
- (A的结果Bob的密码)% 大质数
最后,A和B计算出的结果相同。
3.RSA算法(质数猜想),真是D-H交换的实现,这是一种强大的单向函数。详见wikipedia:http://en.wikipedia.org/wiki/RSA_(algorithm)
把wikipedia上的例子直接搬过来了:
A working example
Here is an example of RSA encryption and decryption. The parameters used here are artificially small, but one can also use OpenSSL to generate and examine a real keypair.
- Choose two distinct prime numbers, such as
-
![p = 61]() and
and ![q = 53]() .
.
-
- Compute n = pq giving
-
- Compute the totient of the product as φ(n)
= (p − 1)(q − 1) giving
-
![\varphi(3233) = (61 - 1)(53 - 1) = 3120]() .
.
-
- Choose any number 1 < e < 3120 that is coprime to
3120. Choosing a prime number for e leaves us only to check that e is not a divisor of 3120.
-
Let
![e = 17.]()
-
Let
- Compute d, the modular multiplicative
inverse of e (mod φ(n)) yielding
-
The public key is (n = 3233, e = 17). For a padded plaintext message m, the encryption function is
The private key is (n = 3233, d = 2753). For an encrypted ciphertext c, the decryption function is c2753(mod 3233).
For instance, in order to encrypt m = 65, we calculate
To decrypt c = 2790, we calculate
-
![m \equiv 2790^{2753} \text{ (mod } 3233\text{)} \equiv 65 \]() .
.
原理:来自isnowfy的一篇博文:http://www.isnowfy.com/application-tonumber-theory-and-introduction-to-rsa/
具体可以过去看,自己推一遍,确实是这样。
参考:1.http://blog.jobbole.com/45530/
2.http://www.isnowfy.com/application-tonumber-theory-and-introduction-to-rsa/
3.http://en.wikipedia.org/wiki/Diffie_hellman

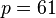 and
and 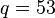 .
.
 .
.


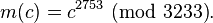
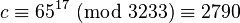
 .
.
 浙公网安备 33010602011771号
浙公网安备 33010602011771号