【神经网络与深度学习】【计算机视觉】Fast R-CNN
首先声明:本文很多内容来自两个博客: RCNN, Fast-RCNN, Faster-RCNN的一些事目标检测--从RCNN到Faster RCNN 串烧 。
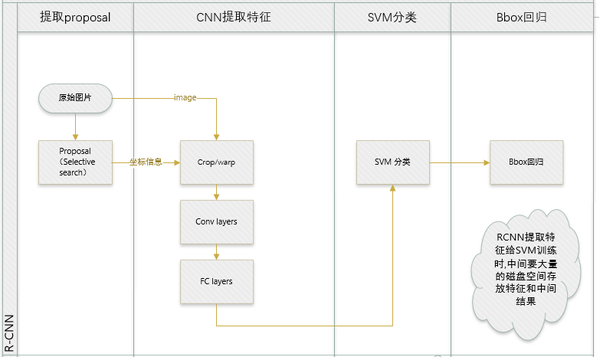
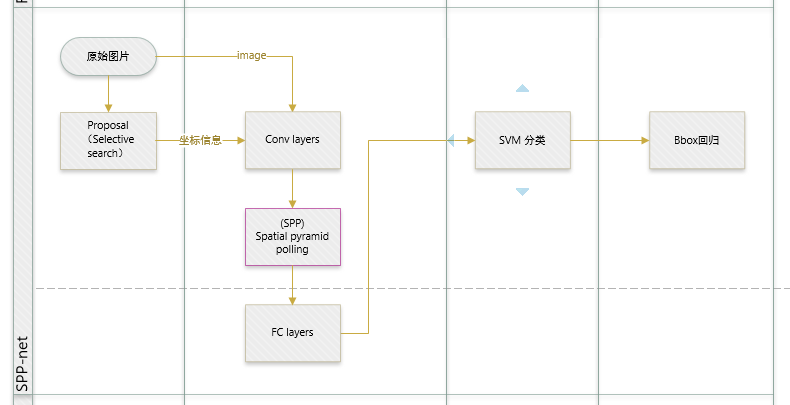
先回归一下: R-CNN ,SPP-net
R-CNN和SPP-net在训练时pipeline是隔离的:提取proposal,CNN提取特征,SVM分类,bbox regression。
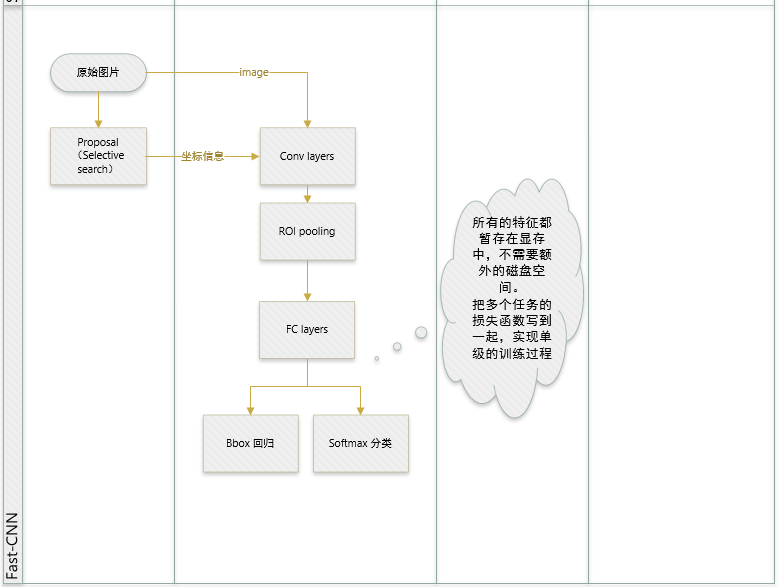
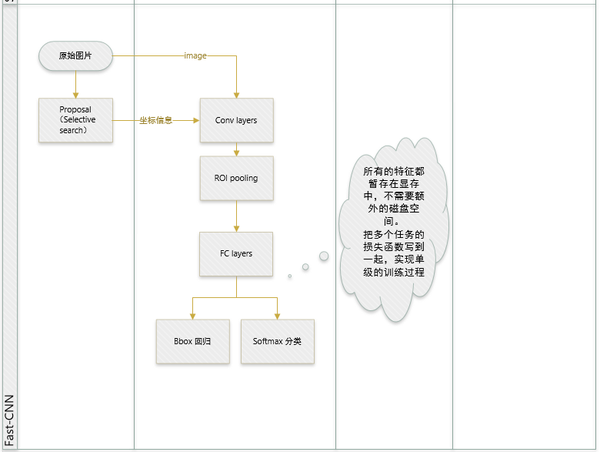
Fast R-CNN 两大主要贡献点 :
-
1 实现大部分end-to-end训练(提proposal阶段除外): 所有的特征都暂存在显存中,就不需要额外的磁盘空。
- joint training (SVM分类,bbox回归 联合起来在CNN阶段训练)把最后一层的Softmax换成两个,一个是对区域的分类Softmax(包括背景),另一个是对bounding box的微调。这个网络有两个输入,一个是整张图片,另一个是候选proposals算法产生的可能proposals的坐标。(对于SVM和Softmax,论文在SVM和Softmax的对比实验中说明,SVM的优势并不明显,故直接用Softmax将整个网络整合训练更好。对于联合训练: 同时利用了分类的监督信息和回归的监督信息,使得网络训练的更加鲁棒,效果更好。这两种信息是可以有效联合的。)
-
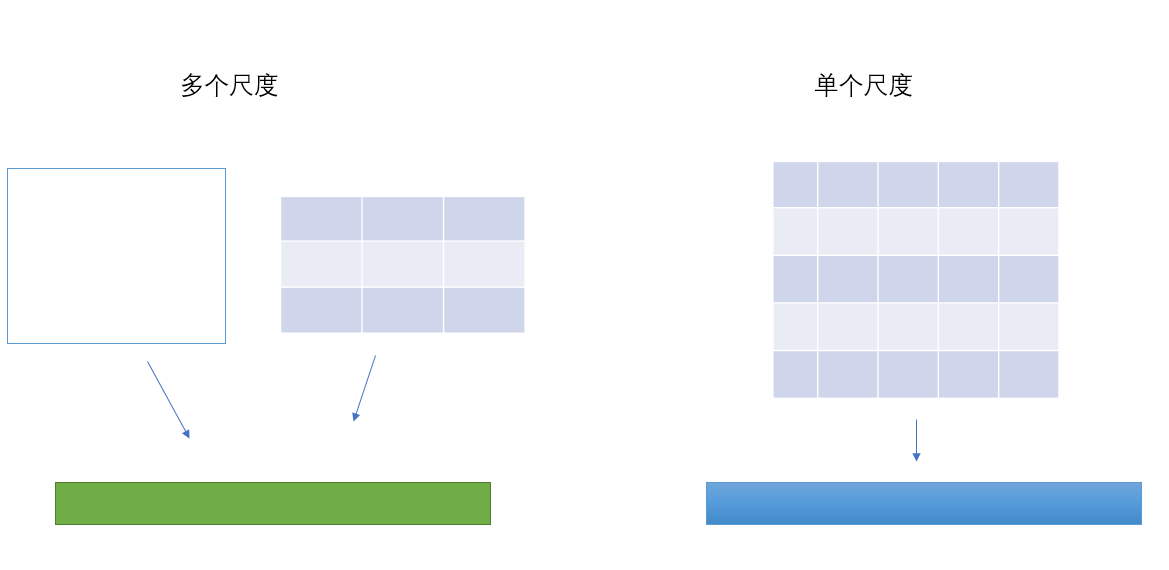
2 提出了一个RoI层,算是SPP的变种,SPP是pooling成多个固定尺度,RoI只pooling到单个固定的尺度 (论文通过实验得到的结论是多尺度学习能提高一点点mAP,不过计算量成倍的增加,故单尺度训练的效果更好。)
其它贡献点:
- 指出SPP-net训练时的不足之处,并提出新的训练方式,就是把同张图片的prososals作为一批进行学习,而proposals的坐标直接映射到conv5层上,这样相当于一个batch一张图片的所以训练样本只卷积了一次。文章提出他们通过这样的训练方式或许存在不收敛的情况,不过实验发现,这种情况并没有发生。这样加快了训练速度。 (实际训练时,一个batch训练两张图片,每张图片训练64个RoIs(Region of Interest))
注意点:
- 论文在回归问题上并没有用很常见的2范数作为回归,而是使用所谓的鲁棒L1范数作为损失函数。
- 论文将比较大的全链接层用SVD分解了一下使得检测的时候更加迅速。虽然是别人的工作,但是引过来恰到好处(矩阵相关的知识是不是可以在检测中发挥更大的作用呢?)。
ROI Pooling
与SPP的目的相同:如何把不同尺寸的ROI映射为固定大小的特征。ROI就是特殊的SPP,只不过它没有考虑多个空间尺度,只用单个尺度(下图只是大致示意图)。
ROI Pooling的具体实现可以看做是针对ROI区域的普通整个图像feature map的Pooling,只不过因为不是固定尺寸的输入,因此每次的pooling网格大小得手动计算,比如某个ROI区域坐标为,那么输入size为 ,如果pooling的输出size为 ,那么每个网格的size为 。
Bounding-box Regression
有了ROI Pooling层其实就可以完成最简单粗暴的深度对象检测了,也就是先用selective search等proposal提取算法得到一批box坐标,然后输入网络对每个box包含一个对象进行预测,此时,神经网络依然仅仅是一个图片分类的工具而已,只不过不是整图分类,而是ROI区域的分类,显然大家不会就此满足,那么,能不能把输入的box坐标也放到深度神经网络里然后进行一些优化呢?rbg大神于是又说了"yes"。在Fast-RCNN中,有两个输出层:第一个是针对每个ROI区域的分类概率预测,第二个则是针对每个ROI区域坐标的偏移优化 ,是多类检测的类别序号。这里我们着重介绍第二部分,即坐标偏移优化。
假设对于类别,在图片中标注了一个groundtruth坐标:,而预测值为 ,二者理论上越接近越好,这里定义损失函数:
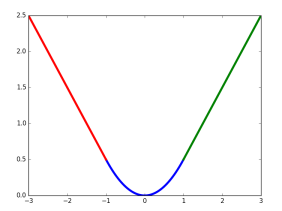
这里, 中的x即为 即对应坐标的差距。该函数在 (−1,1) 之间为二次函数,而其他区域为线性函数,作者表示这种形式可以增强模型对异常数据的鲁棒性,整个函数在matplotlib中画出来是这样的
对应的代码在smooth_L1_loss_layer.cu中。


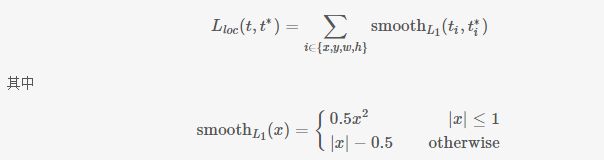

 浙公网安备 33010602011771号
浙公网安备 33010602011771号