【神经网络与深度学习】卷积与反卷积

这里写图片描述 

1. 卷积与反卷积

如上图演示了卷积核反卷积的过程，定义输入矩阵为 I（4×4），卷积核为 K（3×3），输出矩阵为 O（2×2）：

  • 卷积的过程为：Conv(I,W)=O
  • 反卷积的过称为：Deconv(W,O)=I（需要对此时的 O 的边缘进行延拓 padding）

2. 步长与重叠

卷积核移动的步长（stride）小于卷积核的边长（一般为正方行）时，变会出现卷积核与原始输入矩阵作用范围在区域上的重叠（overlap），卷积核移动的步长（stride）与卷积核的边长相一致时，不会出现重叠现象。

4×4 的输入矩阵 I和 3×3 的卷积核K：

  • 在步长（stride）为 1 时，输出的大小为 (4−3+1)×(4−3+1)

现考虑其逆问题，原始输入矩阵为多大时，其与 3×3 的卷积核K 相卷积得到的输出矩阵的大小为 4×4：

  • 步长（stride）为 1 时，(x−3+1)×(x−3+1)=4×4 
    • x=6

搞明白了卷积网络中所谓deconv到底是个什么东西后，不写下来怕又忘记，根据参考资料，加上我自己的理解，记录在这篇博客里。

先来规范表达

  • 为了方便理解，本文出现的举例情况都是2D矩阵卷积，卷积输入和核形状都为正方形，x和y轴方向的padding相同，stride也相同。
  • 记号： 
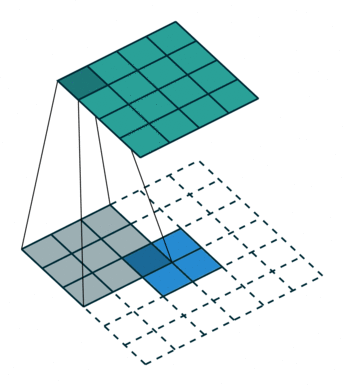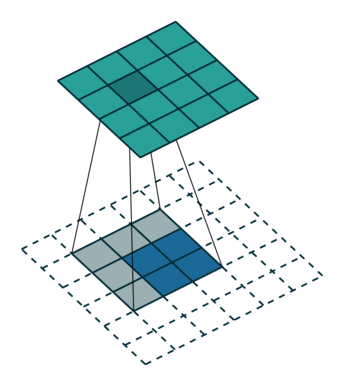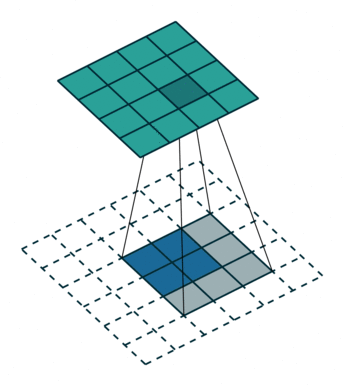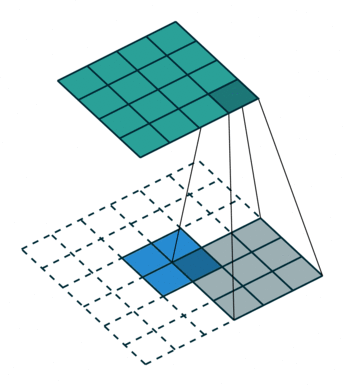
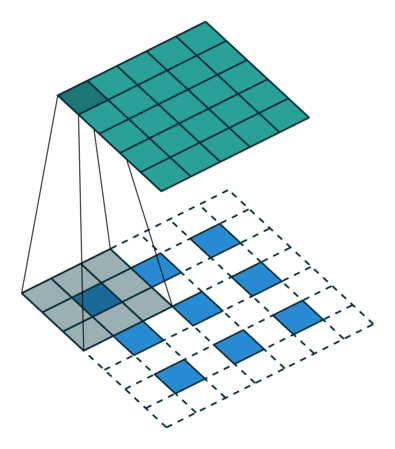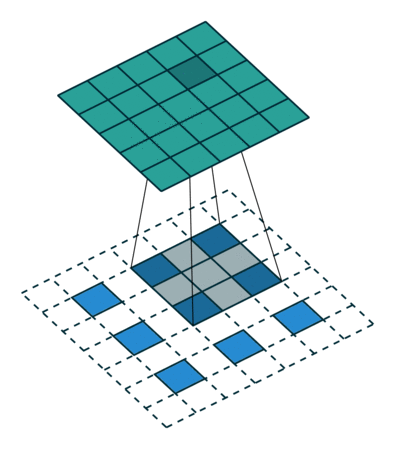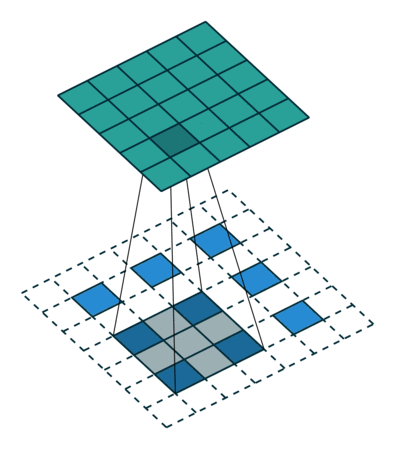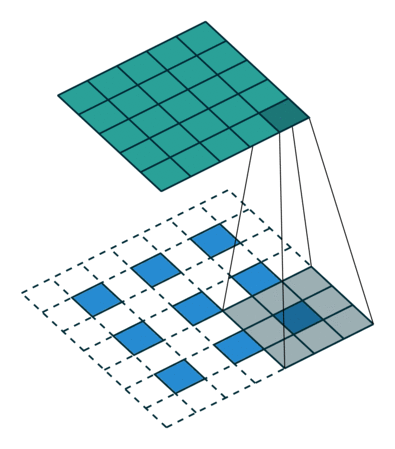
     i,o,k,p,s 分别表示：卷积/反卷积的输入大小 input size，卷积/反卷积输出大小 output size，卷积/反卷积核大小 kernel size， padding， stride 。
  • 举例（如下左图）： 
    输入 X∈R(4,4)矩阵，卷积核 w∈R(3,3)，padding=0，stride=1的情况下，卷积的输出 Y∈R(2,2)，就记为 i=4,o=2,k=3,p=0,s=1 。

推翻错误的理解

第一次看到deconv这个词，以为deconv的结果就是卷积的逆，觉得神奇，不禁产生了“哦？转置的卷积就可以求逆了吗？”这样的想法，然后在matlab里面实验求证，我还记得当时以为反卷积能够求逆，考虑到图片进行常规卷积操作输出大小又不可能变大（same/valid），于是我还假设反卷积输出大小不变，用了same padding和原核的转置作为反卷积配置，结果发现根本不是那么一回事好吗。 
其实DL中的deconv，是一种上采样过程，举个比方：输入 X∈R(4,4)矩阵，卷积核 w∈R(3,3)，pad=0，stride=1的情况下（如下左图），卷积的输出 Y∈R(2,2)。对 Y进行deconv，它只能做到把还原输出大小到和 X一样大，输出值和 X有那么一点联系。 
所以啊deconv这个名字相当误导人呐！这在cs231n课程里也被吐槽过，大家现在更喜欢用transposed conv来表述反卷积。为了方便起见，后文就用反卷积这个词了。

第二个容易confused的地方，就是很多文章都说卷积核的转置就可以求反卷积，又陷入迷茫“就算把卷积核转置（或者左右翻转上下翻转），卷积后输出还是越来越小（或不变，至少不会增大）啊”……直到看到文献和相应的这个动画（其他动画在github-convolution arithmetic1）

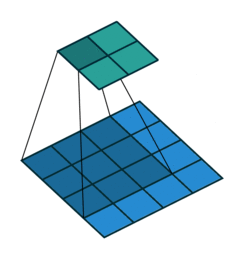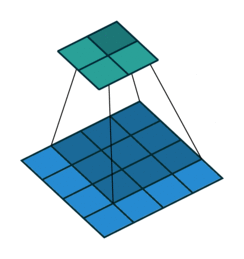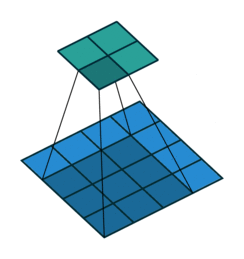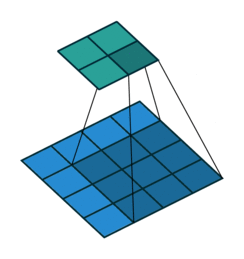卷积 $\ padding=0,stride=1$ 反卷积$\ padding=0,stride=1$
卷积  i=4,k=3,p=0,s=1,则 o=2 反卷积 i=2,k=3,p=0,s=1,则 o=4

注意图中蓝色（下面）是输入，绿色（上面）是输出，卷积和反卷积在 p、s、k 等参数一样时，是相当于 i 和 o 调了个位。 
这里说明了反卷积的时候，是有补0的，即使人家管这叫no padding（ p=0），这是因为卷积的时候从蓝色 4×4 缩小为绿色 2×2，所以对应的 p=0 反卷积应该从蓝色 2×2 扩展成绿色 4×4。而且转置并不是指这个 3×3 的核 w 变为 wT，但如果将卷积计算写成矩阵乘法（在程序中，为了提高卷积操作的效率，就可以这么干，比如tensorflow中就是这种实现）， Y⃗ =CX⃗ （其中 Y⃗  表示将 Y⃗  拉成一维向量， X⃗  同理），那么反卷积确实可以表示为 CTY⃗ ，而这样的矩阵乘法，恰恰等于 w 左右翻转再上下翻转后与补0的 Y 卷积的情况。

然后就产生了第三个confuse：“补0了会不会有影响，还能通过反卷积近似输入 X 吗？”其实反卷积也不一定能达到近似的效果，图像里的卷积，相当于一种相关操作，而反卷积维持了这种相关操作时的 w 与 X、与 Y 之间的联系维持了。至于补0后操作是否还等价，上一段已经说明了是等价的，读者可以在阅读完后面的文章后自己尝试一下。

反卷积以及反向传播的过程

卷积和反卷积的过程在arXiv-A guide to convolution arithmetic for deep learning2写的非常详细，还有很多例子便于理解，在这里我就截图出重点来（ps.文中的figure2.1就是上图的左边）。剩下的例子请大家多看看原文，最好自己动手算一下，我也贴个我算的过程（ Ci 表示矩阵 C 的第 i 行），供参考。 
关于反向传播， 知乎-如何理解深度学习中的deconvolution networks3有详细的推导过程。 
这里写图片描述 
这里写图片描述
这里写图片描述 
这里写图片描述 
这里写图片描述

参考资料

  1. https://github.com/vdumoulin/conv_arithmetic#convolution-arithmetic ↩
  2. https://arxiv.org/abs/1603.07285 ↩
  3. https://www.zhihu.com/question/43609045?sort=created ↩

Transposed Convolution, Fractionally Strided Convolution or Deconvolution

 Posted on 2016-10-29





反卷积（Deconvolution）的概念第一次出现是Zeiler在2010年发表的论文Deconvolutional networks中，但是并没有指定反卷积这个名字，反卷积这个术语正式的使用是在其之后的工作中(Adaptive deconvolutional networks for mid and high level feature learning)。随着反卷积在神经网络可视化上的成功应用，其被越来越多的工作所采纳比如：场景分割、生成模型等。其中反卷积（Deconvolution）也有很多其他的叫法，比如：Transposed Convolution，Fractional Strided Convolution等等。

这篇文章的目的主要有两方面：
1. 解释卷积层和反卷积层之间的关系；
2. 弄清楚反卷积层输入特征大小和输出特征大小之间的关系。

## 卷积层

卷积层大家应该都很熟悉了,为了方便说明，定义如下：
- 二维的离散卷积（N=2N=2）
- 方形的特征输入（i1=i2=ii1=i2=i）
- 方形的卷积核尺寸（k1=k2=kk1=k2=k）
- 每个维度相同的步长（s1=s2=ss1=s2=s）
- 每个维度相同的padding (p1=p2=pp1=p2=p)

下图表示参数为 (i=5,k=3,s=2,p=1)(i=5,k=3,s=2,p=1) 的卷积计算过程，从计算结果可以看出输出特征的尺寸为 (o1=o2=o=3)(o1=o2=o=3)。


下图表示参数为 (i=6,k=3,s=2,p=1)(i=6,k=3,s=2,p=1) 的卷积计算过程，从计算结果可以看出输出特征的尺寸为 (o1=o2=o=3)(o1=o2=o=3)。



从上述两个例子我们可以总结出卷积层输入特征与输出特征尺寸和卷积核参数的关系为：

o=⌊i+2p−ks⌋+1.o=⌊i+2p−ks⌋+1.

其中 ⌊x⌋⌊x⌋ 表示对 xx 向下取整。

反卷积层

在介绍反卷积之前，我们先来看看卷积运算和矩阵运算之间的关系。

卷积和矩阵相乘

考虑如下一个简单的卷积层运算，其参数为 (i=4,k=3,s=1,p=0)(i=4,k=3,s=1,p=0)，输出 o=2o=2。



对于上述卷积运算，我们把上图所示的3×3卷积核展成一个如下所示的[4,16]的稀疏矩阵 CC， 其中非0元素 wi,jwi,j 表示卷积核的第 ii 行和第 jj 列。

⎛⎝⎜⎜⎜⎜w0,0000w0,1w0,000w0,2w0,1000w0,200w1,00w0,00w1,1w1,0w0,1w0,0w1,2w1,1w0,2w0,10w1,20w0,2w2,00w1,00w2,1w2,0w1,1w1,0w2,2w2,1w1,2w1,10w2,20w1,200w2,0000w2,1w2,000w2,2w2,1000w2,2⎞⎠⎟⎟⎟⎟(w0,0w0,1w0,20w1,0w1,1w1,20w2,0w2,1w2,2000000w0,0w0,1w0,20w1,0w1,1w1,20w2,0w2,1w2,200000000w0,0w0,1w0,20w1,0w1,1w1,20w2,0w2,1w2,2000000w0,0w0,1w0,20w1,0w1,1w1,20w2,0w2,1w2,2)

我们再把4×4的输入特征展成[16,1]的矩阵 XX，那么 Y=CXY=CX 则是一个[4,1]的输出特征矩阵，把它重新排列2×2的输出特征就得到最终的结果，从上述分析可以看出卷积层的计算其实是可以转化成矩阵相乘的。值得注意的是，在一些深度学习网络的开源框架中并不是通过这种这个转换方法来计算卷积的，因为这个转换会存在很多无用的0乘操作，Caffe中具体实现卷积计算的方法可参考Implementing convolution as a matrix multiplication。

通过上述的分析，我们已经知道卷积层的前向操作可以表示为和矩阵CC相乘，那么 我们很容易得到卷积层的反向传播就是和CC的转置相乘。

反卷积和卷积的关系

全面我们已经说过反卷积又被称为Transposed(转置) Convolution，我们可以看出其实卷积层的前向传播过程就是反卷积层的反向传播过程，卷积层的反向传播过程就是反卷积层的前向传播过程。因为卷积层的前向反向计算分别为乘 CC 和 CTCT,而反卷积层的前向反向计算分别为乘 CTCT 和 (CT)T(CT)T ，所以它们的前向传播和反向传播刚好交换过来。

下图表示一个和上图卷积计算对应的反卷积操作，其中他们的输入输出关系正好相反。如果不考虑通道以卷积运算的反向运算来计算反卷积运算的话，我们还可以通过离散卷积的方法来求反卷积（这里只是为了说明，实际工作中不会这么做）。

同样为了说明，定义反卷积操作参数如下：

  • 二维的离散卷积（N=2N=2）
  • 方形的特征输入（i′1=i′2=i′i1′=i2′=i′）
  • 方形的卷积核尺寸（k′1=k′2=k′k1′=k2′=k′）
  • 每个维度相同的步长（s′1=s′2=s′s1′=s2′=s′）
  • 每个维度相同的padding (p′1=p′2=p′p1′=p2′=p′)

下图表示的是参数为( i′=2,k′=3,s′=1,p′=2i′=2,k′=3,s′=1,p′=2)的反卷积操作，其对应的卷积操作参数为 (i=4,k=3,s=1,p=0)(i=4,k=3,s=1,p=0)。我们可以发现对应的卷积和非卷积操作其 (k=k′,s=s′)(k=k′,s=s′)，但是反卷积却多了p′=2p′=2。通过对比我们可以发现卷积层中左上角的输入只对左上角的输出有贡献，所以反卷积层会出现 p′=k−p−1=2p′=k−p−1=2。通过示意图，我们可以发现，反卷积层的输入输出在 s=s′=1s=s′=1 的情况下关系为：

o′=i′−k′+2p′+1=i′+(k−1)−2po′=i′−k′+2p′+1=i′+(k−1)−2p



Fractionally Strided Convolution

上面也提到过反卷积有时候也被叫做Fractionally Strided Convolution，翻译过来大概意思就是小数步长的卷积。对于步长 s>1s>1的卷积，我们可能会想到其对应的反卷积步长 s′<1s′<1。 如下图所示为一个参数为 i=5,k=3,s=2,p=1i=5,k=3,s=2,p=1的卷积操作(就是第一张图所演示的)所对应的反卷积操作。对于反卷积操作的小数步长我们可以理解为：在其输入特征单元之间插入 s−1s−1 个0，插入0后把其看出是新的特征输入，然后此时步长 s′s′ 不再是小数而是为1。因此，结合上面所得到的结论，我们可以得出Fractionally Strided Convolution的输入输出关系为：

o′=s(i′−1)+k−2po′=s(i′−1)+k−2p



参考

conv_arithmetic

Is the deconvolution layer the same as a convolutional layer?



posted @ 2017-12-13 15:07  ZhangPYi  阅读(5045)  评论(0)  编辑  收藏  举报