牛顿迭代法求解平方根

 

迭代简介

迭代，是一种数值方法，具体指从一个初始值，一步步地通过迭代过程，逐步逼近真实值的方法。
与之相对的是直接法，也就是通过构建解析解，一步求出问题的方法。

通常情况下，我们总是喜欢一步得到问题的结果，因此直接法总是优先考虑的。
但是，当遇到复杂的问题时，特别在未知量很多，方程非线性时，无法得到直接解法（例如五次方程并没有解析解）。
这时候，我们需要使用迭代算法，一步步逼近，得到问题的答案。

牛顿迭代法

牛顿迭代法简介

牛顿迭代法，求解如下问题的根x

 

f(x)=0

 

求解方法如下：

 

 

 

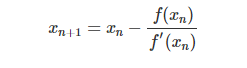
方法中，迭代变量是根x ，迭代关系式如上，迭代终止条件是:

                             

 

牛顿迭代法需要满足的条件是：
f′(x) 是连续的，并且待求的零点x 是孤立的。
那么，在零点x 周围存在一个区域，只要初始值x0 位于这个邻域内，那么牛顿法必然收敛。
并且，如果f′(x) 不为0，那么牛顿法将具有平方收敛的特性，也就是，每迭代一次，其结果的有效倍数将增加一倍。

简单推导

 

 

#include"iostream"
#include"map"
#include"cmath"
#include"string"
using namespace std;

int sortt( int x){
    double t = 1.0;
    while(fabs(t * t - x) > 1e-6){
        t = (t + x / t) / 2;
    }
    return t;
}

int main(){
    int x;
    while(cin>>x){
        cout<<sortt(x)<<endl;
    }
    return 0;
} 

 

 

本文转自：http://blog.csdn.net/young_gy/article/details/45766433