聚类算法

聚类算法

李鑫 2014210820 电子系

1、kmeans算法

1.1Kmeans算法理论基础

         K均值算法能够使聚类域中所有样品到聚类中心距离平方和最小。其原理为：先取k个初始聚类中心，计算每个样品到这k个中心的距离，找出最小距离，把样品归入最近的聚类中心，修改中心点的值为本类所有样品的均值，再计算各个样品到新的聚类中心的距离，重新归类，修改新的中心点，直到新的聚类中心和上一次聚类中心差距很小时结束。此算法结果受到聚类中心的个数和聚类中心初次选择影响，也受到样品的几个性质及排列次序的影响。如果样品的几何性质表明它们能形成几块孤立的区域，则算法一般可以收敛。

1.2Kmeans算法实现步骤

①产生二维高斯数据，设置聚类中心数N

②随机取N个点作为聚类中心。

③计算其余样品到这N个聚类中心的距离，将他们归到最近的类，到所有的样品都归完类。

④计算各个类样品的平均值作为该类新的聚类中心，再计算所有样品到新的聚类中心的距离，把他们归到最近的类，如此反复，直到聚类中心不再变化为止。

1.3Kmeans算法编程实现

clear all;close all;clc;

% 第一组数据

mu1=[0 0 ];  %均值

S1=[.1 0 ;0 .1];  %协方差

data1=mvnrnd(mu1,S1,100);   %产生高斯分布数据

%第二组数据

mu2=[1.25 1.25 ];

S2=[.1 0 ;0 .1];

data2=mvnrnd(mu2,S2,100);

% 第三组数据

mu3=[-1.25 1.25 ];

S3=[.1 0 ;0 .1];

data3=mvnrnd(mu3,S3,100);

% 显示数据

plot(data1(:,1),data1(:,2),'b+');

hold on;

plot(data2(:,1),data2(:,2),'r+');

plot(data3(:,1),data3(:,2),'g+');

grid on;

%  三类数据合成一个不带标号的数据类

data=[data1;data2;data3]; 

N=3;%设置聚类数目

[m,n]=size(data);

pattern=zeros(m,n+1);

center=zeros(N,n);%初始化聚类中心

pattern(:,1:n)=data(:,:);

for x=1:N

    center(x,:)=data( randi(300,1),:);%第一次随机产生聚类中心

end

while 1

distence=zeros(1,N);

num=zeros(1,N);

new_center=zeros(N,n);

 

for x=1:m

    for y=1:N

    distence(y)=norm(data(x,:)-center(y,:));%计算到每个类的距离

    end

    [~, temp]=min(distence);%求最小的距离

    pattern(x,n+1)=temp;         

end

k=0;

for y=1:N

    for x=1:m

        if pattern(x,n+1)==y

           new_center(y,:)=new_center(y,:)+pattern(x,1:n);

           num(y)=num(y)+1;

        end

    end

    new_center(y,:)=new_center(y,:)/num(y);

    if norm(new_center(y,:)-center(y,:))<0.1

        k=k+1;

    end

end

if k==N

     break;

else

     center=new_center;

end

end

[m, n]=size(pattern);

 

%最后显示聚类后的数据

figure;

hold on;

for i=1:m

    if pattern(i,n)==1 

         plot(pattern(i,1),pattern(i,2),'r*');

         plot(center(1,1),center(1,2),'ko');

    elseif pattern(i,n)==2

         plot(pattern(i,1),pattern(i,2),'g*');

         plot(center(2,1),center(2,2),'ko');

    elseif pattern(i,n)==3

         plot(pattern(i,1),pattern(i,2),'b*');

         plot(center(3,1),center(3,2),'ko');

    elseif pattern(i,n)==4

         plot(pattern(i,1),pattern(i,2),'y*');

         plot(center(4,1),center(4,2),'ko');

    else

         plot(pattern(i,1),pattern(i,2),'m*');

         plot(center(4,1),center(4,2),'ko');

    end

end

grid on;

1.3Kmeans算法测试结果：

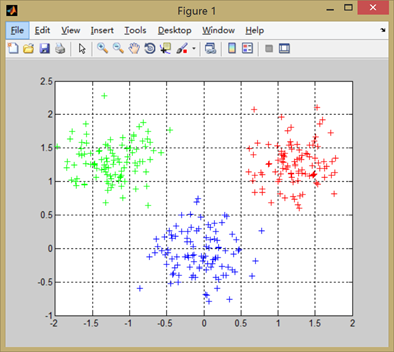
a)高斯数对                                   b)N=2

c) N=3                             d)N=4

    e)N=5                                   f)N=6

可以看到聚类数目N对聚类有一定影响，同时在N相同的情况下每次的聚类结果也不完全一样，说明初始的聚类中心对聚类结果也有一定影响。

2层次聚类算法

层次聚类算法分为合并算法和分裂算法。合并算法会在每一步减少聚类中心的数量，聚类产生的结果来自前一步的两个聚类的合并；分裂算法与合并算法原理相反，在每一步增加聚类的数量，每一步聚类产生的结果都将是前一步聚类中心分裂得到的。合并算法现将每个样品自成一类，然后根据类间距离的不同，合并距离小于阈值的类。我用了基于最短距离算法的层次聚类算法，最短距离算法认为，只要两个类的最小距离小于阈值，就将两个类合并成一个类。

2.1层次聚类算法实现步骤

①获得所有样品特征

②设置阈值

③将所有样品各分一类，聚类中心等于样品总个数。

④对所有样品循环：

         找到距离最近的两类pi，pj，设置距离minDis

         若minDis<=T，则合并pi和pj否则退出循环。

2.2层次聚类算法的编程实现

clear all;close all;clc;

% 第一类数据

mu1=[0 0 ];  %均值

S1=[0.1 0 ;0 0.1];  %协方差

data1=mvnrnd(mu1,S1,100);   %产生高斯分布数据

%第二类数据

mu2=[1.25 1.25 ];

S2=[0.1 0 ;0 0.1];

data2=mvnrnd(mu2,S2,100);

% 第三个类数据

mu3=[-1.25 1.25 ];

S3=[0.1 0 ;0 0.1];

data3=mvnrnd(mu3,S3,100);

% 显示数据

plot(data1(:,1),data1(:,2),'b+');

hold on;

plot(data2(:,1),data2(:,2),'r+');

plot(data3(:,1),data3(:,2),'g+');

grid on;

%  三类数据合成一个不带标号的数据类

data=[data1;data2;data3]; 

[m,n]=size(data);

patternNum=m;

T=0.1;

pattern=zeros(m,n+1);

for i=1:patternNum

    pattern(i,n+1)=i;

    pattern(i,1:n)=data(i,:);

end

while 1

    minDis=inf;

    pi=0;

    pj=0;

%     寻找距离最近的两个类计算最小距离

    for i=1:patternNum-1

        for j=i+1:patternNum

            if(pattern(i,n+1)~=pattern(j,n+1))

                tempDis=norm(pattern(i,1:n)-pattern(j,1:n));

                if(tempDis<minDis)

                    minDis=tempDis;

                    pi=pattern(i,n+1);

                    pj=pattern(j,n+1);

                end

            end

        end

    end

%     距离小于阈值则合并两个类

    if(minDis<=T)

        if(pi>pj)

            temp=pi;

            pi=pj;

            pj=temp;

        end

        for i=1:patternNum

            if(pattern(i,n+1)==pi)

                pattern(i,n+1)=pi;

            elseif(pattern(i,n+1)>pi)

                pattern(i,n+1)=pattern(i,n+1)-1;

            end

        end

    else

        break;

    end

end

disp('ok')

[m, n]=size(pattern);

%最后显示聚类后的数据

figure;

hold on;

for i=1:m

    if pattern(i,n)==1 

         plot(pattern(i,1),pattern(i,2),'r*');

    elseif pattern(i,n)==2

         plot(pattern(i,1),pattern(i,2),'g*');

    elseif pattern(i,n)==3

         plot(pattern(i,1),pattern(i,2),'b*');

    elseif pattern(i,n)==4

         plot(pattern(i,1),pattern(i,2),'y*');

    else

         plot(pattern(i,1),pattern(i,2),'m*');

    end

end

grid on;

2.3层次聚类算法测试结果：

下图是产生的高斯数对及当阈值设置为T=0.1的时候的结果：

当T=0.5时的结果：

可见当阈值设的比较大时所有的都将成为一类。所以阈值的设置很重要。

基于最小距离的层次聚算法对类间距要求很高，例如将高斯数对的协方差加大，产生距离比较近的数对时，层次聚类算法就会出现很大问题如下图：

但是在相同的生成参数下，kmeans却有很好的效果：

3基于kmeans的图像分割

Kmeans之前已经讲过了，其图像分割只不过是把之前的高斯数对换成图像二维像素点，彩色图像每个像素点有rgb三个分量，灰度图像只有一个分量。

3.1编程实现 

clear;clc;close all;

data=imread('src1.bmp');

imshow(data)

[m,n,c]=size(data);

[mu,pattern]=k_mean_Seg(data,2);

for x=1:m

    for y=1:n

        if pattern(x,y,1)==1

            data(x,y,1)=0;

            data(x,y,2)=0;

            data(x,y,3)=255;

        elseif pattern(x,y,1)==2

            data(x,y,1)=0;

            data(x,y,2)=255;

            data(x,y,3)=0;

        elseif pattern(x,y,1)==3

            data(x,y,1)=255;

            data(x,y,2)=0;

            data(x,y,3)=0;

        else

            data(x,y,1)=255;

            data(x,y,2)=255;

            data(x,y,3)=0;

        end

    end

end

figure;

imshow(data);  

 

function [num,mask]=k_mean_Seg(src,k)

src=double(src);

img=src;       

src=src(:);     

mi=min(src);    

src=src-mi+1;   

L=length(src);

 

m=max(src)+1;

hist=zeros(1,m);

histc=zeros(1,m);

for i=1:L

  if(src(i)>0)

      hist(src(i))=hist(src(i))+1;

  end;

end

ind=find(hist);

hl=length(ind);

num=(1:k)*m/(k+1);

while(true)

  prenum=num;

  for i=1:hl

      c=abs(ind(i)-num);

      cc=find(c==min(c));

      histc(ind(i))=cc(1);

  end

  for i=1:k,

      a=find(histc==i);

      num(i)=sum(a.*hist(a))/sum(hist(a));

  end

  if(num==prenum)

      break;

  end;

 

end

L=size(img);

mask=zeros(L);

for i=1:L(1),

for j=1:L(2),

  c=abs(img(i,j)-num);

  a=find(c==min(c)); 

  mask(i,j)=a(1);

end

end

num=num+mi-1;     

 

3.2结果展示

  

                                     a)原图                                                                                b)N=2

 

c)N=3                                                                         d)N=4

对于灰度图像，用data=rgb2gray(data); 转化成为成为灰度图像后面的显示换成如下：

for x=1:m

    for y=1:n

        if pattern(x,y)==1

            data(x,y)=0;

        elseif pattern(x,y)==2

            data(x,y,1)=80;

        elseif pattern(x,y)==3

            data(x,y)=180;

        else

            data(x,y)=255;

        end

    end

end

 

a)原图                                                                                b)N=2

 

c)N=3                                                                         d)N=4

4、基于层次聚类算法的图像分割

层次聚类算法前面已经提到，其计算量远远大于kmeans，又由于在MATLAB平台下对多重嵌套的for循环处理速度很慢，并没有得到运行结果。仅将代码附如下：

4.1层次聚类算法的图像分割编程实现

clear;clc;close all;

data=imread('src1.bmp');

data=rgb2gray(data);

imshow(data);

data=double(data);

[m,n]=size(data);

patternNum=m*n;

T=10;

pattern=zeros(m,n);

for x=1:m

    for y=1:n

        for i=1:patternNum

            pattern(x,y)=i;

        end

    end

end

 

while 1

    minDis=inf;

    pi=0;

    pj=0;

%     寻找距离最近的两个类计算最小距离

    for x=1:m

        for y=1:n

            for i=1:m

                for j=1:n

            if(pattern(x,y)~=pattern(i,j))

                tempDis=abs(pattern(x,y)-pattern(i,j));

                if(tempDis<minDis)

                    minDis=tempDis;

                    pi=pattern(x,y);

                    pj=pattern(i,j);

                end

            end

                end

            end

        end

    end

%     距离小于阈值则合并两个类

    if(minDis<=T)

        if(pi>pj)

            temp=pi;

            pi=pj;

            pj=temp;

        end

        for i=1:m

            for j=1:n

            if(pattern(i,j)==pi)

                pattern(i,j)=pi;

            elseif(pattern(i,j)>pi)

                pattern(i,j)=pattern(i,j)-1;

            end

            end

        end

    else

        break;

    end

end

disp('ok')

[m, n]=size(pattern);

 

%最后显示聚类后的数据

for x=1:m

    for y=1:n

        if pattern(x,y)==1

            data(x,y,1)=0;

            data(x,y,2)=0;

            data(x,y,3)=255;

        elseif pattern(x,y)==2

            data(x,y,1)=0;

            data(x,y,2)=255;

            data(x,y,3)=0;

        elseif pattern(x,y)==3

            data(x,y,1)=255;

            data(x,y,2)=0;

            data(x,y,3)=0;

        else

            data(x,y,1)=255;

            data(x,y,2)=255;

            data(x,y,3)=0;

        end

    end

end

figure;

imshow(data);