马氏距离(Mahalanobis distance)

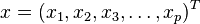　　马氏距离(Mahalanobis distance)是由印度统计学家马哈拉诺比斯（P. C. Mahalanobis）提出的，表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的）并且是尺度无关的（scale-invariant），即独立于测量尺度。 对于一个均值为，协方差矩阵为Σ的多变量矢量，其马氏距离为

 

马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为Σ的随机变量与的差异程度：

 

　　　如果协方差矩阵为单位矩阵，马氏距离就简化为欧式距离；如果协方差矩阵为对角阵，其也可称为正规化的马氏距离。

 

 

其中σi是xi的标准差。

 

基础知识：

假设空间中两点x，y，定义：

欧几里得距离：

Mahalanobis距离：

不难发现，如果去掉马氏距离中的协方差矩阵，就退化为欧氏距离。那么我们就需要探究这个多出来的因子究竟有什么含义。

 

第一个例子基础知识

从下往上的一段50米长的坡道路，下面定一个A点，上面定B一个点。假设有两种情况从A到B：

a)坐手扶电梯上去。

b)从手扶电梯旁边的楼梯爬上去。

两种情况下我们分别会产生两种不同的主观感受，坐电梯轻松愉快，感觉很快就从A到了B——“A与B真近”；走楼梯爬的气喘吁吁很累，感觉走了好久才走到B——“A与B真远”。

 

第二个例子

观看落日之时，由于大气的折射效应，太阳形状产生形变并且视觉位置也比真实位置高。

 

解释

以上两个例子看似和模式识别没有关系，实际上都引入了“相对论”的问题。回到问题本身，欧式距离就好比一个参照值，它表征的是当所有类别等概率出现的情况下，类别之间的距离。此时决策面中心点的位置就是两个类别中心的连线的中点。如图1所示。而当类别先验概率并不相等时，显然，如果仍然用中垂线作为决策线是不合理的，将出现判别错误（绿色类的点被判别为红色类），假设图1中绿色类别的先验概率变大，那么决策线将左移，如图2黄线。左移的具体位置，就是通过马氏距离来获得的。马氏距离中引入的协方差参数，表征的是点的稀密程度。

 

　　从哲学上来说，用马氏距离处理数据时，不再把数据单纯的看作是冷冰冰的数字——那个引入的协方差，承认了客观上的差异性，就好像是有了人类的感情倾向，使得模式识别更加“人性化”也更加“视觉直观”。