KMP原理、分析及C语言实现
(是在matrix67博客基础上整理而来,整理着:华科小涛@http://www.cnblogs.com/hust-ghtao/)
有些算法可以让人发疯,KMP算法就是一个。在网上找了很多资料讲的都让人摸不着头脑,本文试图将此算法的思想及实现讲清楚。分为三个部分:基本思想、next[]数组的求法和代码实现。
1 KMP算法基本思想
KMP算法是用来进行字符串匹配的。在上篇文章中我们介绍了字符串匹配的模式匹配法,我们知道若主串的长度为n,m为要匹配的子串的长度,时间复杂度为O(m*n)。在计算机的运算当中,模式匹配的操作随处可见,而模式匹配算法就太低效了。所以就有人提出了KMP算法,它的复杂度只有O(m+n),之所以叫做KMP算法,是因为这个算法是由Kuuth、Morris、Pratt三个人提出来的,取了他们名字的首字母命名。
为了后续介绍方便,先给出关于字符串的两个概念:“前缀”和“后缀”。“前缀”指除了最后一个字符以外,一个字符串的全部头部组合;“后缀”指除了第一个字符以外,一个字符串的全部尾部组合。如下:
假如母串A=”abababaababacb”,模式串B=”ababacb”,分别以i和j表示其字符的索引,当A[i-j+1…i]与B[1…j]完全相等时,下一次比较A[i+1]和B[j+1],若想等则i和j各加1;若不相等呢?朴素模式匹配算法是通过i值的回溯来继续进行匹配的;KMP的策略是i不进行回溯,在此基础上调整j的位置(减小j值)使得A[i-j+1…i]与B[1…j]仍然相等,并继续比较A[i+1]和B[j+1],若想等则i、j各加1,否则重新调整j的值。
这里有两个关键:KMP算法是正确的吗?若是正确的,调整j的原则是什么 ?对于第一个问题请参考《算法导论》。我们来看第二个问题:调整j的原则。原则当然是为目的服务的,我们的目的是进行匹配字符串,即j在大小变化过程当中,能否从最开始的1变化到m,所以为了尽快达到m,调整后的j当然越大越好。就以A、B匹配为例:
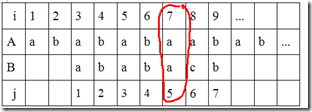
(1)当i=j=5时的情况
此时,A[6]≠B[6],则j不能等于5了,我们要将j减小,减小之后要满足A[5]及其之前的部分仍然匹配。假设j=4可以吗?显然不行A[5]≠B[4] ;j=3呢,满足条件A[5]=B[3] ,于是,i变成了6,而j则变成了 4:
我们发动脑筋仔细想一下,看能不能找到一些规律,对j的值进行调整,也不能挨个试吧!仔细观察上述调整,在j变化之前A[1…5]和B[1…5]完全匹配。调整之后,A[3…5]和
B[1…3]和也完全匹配。也就是说在进行调整时,i保持不变,j变成j',调整后应该满足以A[i]结尾的长度为j'的字符串正好匹配B串的前j各字符,也就是使得A[i-j'+1…i]与B[1…j']仍然相等,调整之前是A[i]结尾的长度为j'的字符串是与B串的后面j'个字符匹配的,调整的过程就是用B串的长度为j'的前缀,代替了B串的长度为j'的后缀的长度,当然为了尽快完成匹配,j'的长度是越大越好。说白了就是当匹配不下去了,就要进行调整,KMP算法要求i的值不能进行回溯,只能调整j值了,当然可以让j从1重新开始,但是之前的匹配就浪费了,能最大限度的避免重复匹配,就找B[1…j]串的前缀和后缀的最长的共有元素,就可以将B串整体后移,用B[1…j]串前缀中的此元素代替后缀中的此元素,由于是同一个串,自然匹配,也就是使得A[i-j'+1…i]与B[1…j']仍然相等。B[1…j']就是此共有元素了,其长度就是j调整后的值。即可以得出结论:当A[i-j+1…i]与B[1…j]完全相等时,下一次比较A[i+1]和B[j+1],若想等则i和j各加1;若不相等呢KMP的策略是i不进行回溯,在此基础上减小j值,调整为B[1…j]串的前缀和后缀的最长共有元素的长度。
为了加深理解,也为了验证上述结论,我们将这个例子完成j=3时,可以发现B[4]、B[5]分别和A[6]、A[7]相等,i变成7,j变成5,比较A[i+1]和B[j+1],A[8]和B[6]不相等,仍需调整j:
j=5,调整为多少合适呢?根据以上结论,应该调整为B[1…5]串即“ababa”,的前缀和后缀的最长共有元素的长度,根据前缀和后缀的概念,“ababa”的前缀有a、ab、aba、abab,后缀有b、ba、aba、baba,最长共有元素为aba,长度为3,所以j应该减小为3:
看下调整之后的结果,A[i-j+1…i]与B[1…j]仍然相等,即A[5…7]和B[1…3]仍然匹配。在比较A[i+1]和B[j+1],即A[8]和B[4]仍不等,需要继续减小j。j当前的值为3,所以我们需要求出B[1…3]这个串的前缀和后缀的最长共有元素的长度,显然“aba”的前缀和后缀的最长共有元素的长度为1,所以j减小为1:
调整之后,A[i-j+1…i]与B[1…j]仍然相等,即A[7]和B[1]仍然匹配。在比较A[i+1]和B[j+1],即A[8]和B[2]仍不等,需要继续减小j。j当前的值为1,所以我们需要求出B[1]这个串的前缀和后缀的最长共有元素的长度,显然“a”的前缀和后缀的最长共有元素的长度为0,所以j减小为0:
再次比较A[i+1]和B[j+1],终于A[8]=B[1],可以发现后面的字符串都能直接匹配,所以匹配成功。事实上,有可能j调整到0,仍然不能满足A[i+1]=B[j+1],那j=0时,我们需要增加i的值,j不变,直到出现,A[i]=B[1]为止。
匹配完了,将算法总结一下吧:当A[i-j+1…i]与B[1…j]完全相等时,下一次比较A[i+1]和B[j+1],若想等则i和j各加1;若不相等呢KMP的策略是i不进行回溯,在此基础上减小j值,调整为B[1…j]串的前缀和后缀的最长共有元素的长度。 我们发现,新的j值取值为多少与iA串无关,至于B串有关。每次进行这里有一个问题需要解决,就是求出B[1…j]串的前缀和后缀的最长共有元素的长度,从而作为j下次的取值,我们将这个长度的值先计算出来,存放到一个next[]数组当中,在进行匹配时直接读取里面的值就好了。假设我们已经求得
next[](下标从1始),其中next[j]表示B[1…j]的前缀和后缀的最长共有元素的长度。则KMP算法的伪代码如下:
1: j=0;
2: for i=1 to n
3: {
4: while (j>0) and (B[j+1]≠A[i])
5: j=next[j] ;
6:
7: if B[j+1]==A[i]
8: j=j+1 ;
9:
10: if j==m then
11: {
12: print('Pattern occurs with shift ',i-m) ;
13: j=next[j] ;
14: }
15: }
16:
最后的j=next[j]是为了上程序继续匹配下去,因为有可能找到多出匹配。毋须多言,上述算法和代码已经讲的很清楚了。我们还遗留了一个问题,就是如何求得next[]数组?
2 next[]数组的求法
对于B=“ababacb”我们如何求它的next[]数组呢,大家肯定会想出各种办法,但时间复杂度有好有坏,不用着急!我们的前辈呢,已经帮我们找到了一个比较好的办法,假设B的长度为m,其复杂度只有O(m),但是还是有点难理解的,先将代码写在这里,然后再做分析:
1: next[1]=0 ;
2: j=0 ;
3: for i = 2 to m
4: {
5: while (j>0) and (B[j+1]≠B[i])
6: j = next[j];
7: if B[j+1]==B[i]
8: j=j+1;
9:
10: next[i]=j ;
11: }
整体思路就是:将next[1]的值赋为1,i值从2到m进行循环,可求出next[2…m],最关键的是while循环里面做的事情。假如已经求得next[1]、next[2]…next[j-1],我们分析求next[j]的过程,这其实是一个递推的过程,就是B串本身的前缀和后缀之间的匹配过程。就已本例来说明求next[]串的方法:
(1)初始化next[1]=2;
(2)i=2,j=0, while循环条件不成立,if语句:B[1]=a≠B[2]=b,则执行next[i]=j,得到next[2]=0;
(3)i=3,j=0,while循环条件不成立,if语句:B[1]=a=B[3],则j=j+1,j为1,则执行next[i]=j, 得到next[3]=1;
(4)i=4,j=1,while循环条件不成立,if语句:B[2]=a=B[4],则j=j+1,j为2,则执行next[i]=j, 得到next[4]=2;
(5)i=5,j=2,while循环条件不成立,if语句:B[3]=a=B[5],则j=j+1,j为3,则执行next[i]=j, 得到next[5]=3;
(6)i=6,j=3,while循环条件成立:
注意这里进行判断,是判断B[i]和B[j+1]是否相等,即B[j+1]即B[next[i-1]+1],next[i-1]就是B[1…i-1]的前后缀最大共有元素的长度,这里由于next[5]=3,所以是判断B[5]
和B[3+1]是否相等,由上图看出不相等。如果相等,next[i]=next[i-1]+1,因为B[1…i-1]的长度为next[i-1]的前缀和长度为next[i-1]的后缀是匹配的,若这个前缀的下一个元素B[next[i-1]+1]和这个后缀的下一个元素B[i]相等,说明B[1…i]的前后追最大共有元素的长度为next[i-1]+1。
到这还可以理解,但是B[i]和B[j+1]不相等,即B[6]≠B[4],我们看上述程序,i=6,j=3,执行的语句是 j=next[j],即j=1:
我们先看前一个图,由于next[5] =3,所以想让B[1…5]的前后缀的最大共有元素进行匹配,在判断前缀和后缀后面的元素是否匹配,如果匹配的话,next[i]=next[i-1]+1。
如果不想等,也是要调整j的值,调整的思想和KMP主程序的思想一样,都是将j减小到B[1…j]的前后缀的最大共有元素,用前缀代替后缀,继续进行匹配。
3 算法复杂度
KMP算法的复杂度O(m+n)。这个算法分成两部分:主程序和求next[]数组的部分。我们先来分析主程序的复杂度:假设主串的长度为n,主要的争议在于,while循环使得执行次数出现了不确定因素。我们将用到时间复杂度的摊还分析中的主要策略,简单地说就是通过观察某一个变量或函数值的变化来对零散的、杂乱的、不规则的执行次数进行累计。KMP的时间复杂度分析可谓摊还分析的典型。我们从上述程序的j 值入手。每一次执行while循环都会使j减小(但不能减成负的),而另外的改变j值的地方只有第8行。每次执行了这一行,j都只能加1;因此,整个过程中j最多加了n个1。于是,j最多只有n次减小的机会(j值减小的次数当然不能超过n,因为j永远是非负整数)。这告诉我们,while循环总共最多执行了n次。按照摊还分析的说法,平摊到每次for循环中后,一次for循环的复杂度为O(1)。整个过程显然是O(n)的。这样的分析对于后面P数组预处理的过程同样有效,同样可以得到预处理过程的复杂度为O(m)。所以KMP算法的复杂度O(m+n)。