腾讯笔试题20210321
一、链表树
时间限制:C/C++ 1秒,其他语言 2秒
空间限制:C/C++ 262144K,其他语言 524288K
64bit IO Format: %lld
题目描述
在牛牛所在的世界,链表是一种二叉树。
这是牛牛第一次见到链表树,他感到十分好奇,他提出了若干个问题,每次询问点x到根的路径上所有点分别是什么,你需要按照深度从小到大给出。
本题为核心代码模式,代码框中预设代码已经指定好类名、方法名、参数名,请勿修改或重新命名,直接返回值即可。
输入
{1, 2, 3, 4, 5, 6, 7}, [1, 2, 3, 4, 5, 6, 7]
输出
[{1}, {1, 2}, {1, 3}, {1, 2, 4}, {1, 2, 5}, {1, 3, 6}, {1, 3, 7}]
说明
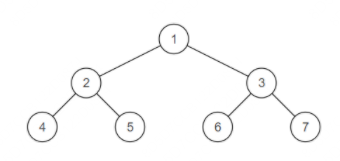
点1到根的路径上的个分别为{1}
点2到根的路径上的个分别为{1, 2}
点3到根的路径上的个分别为{1, 3}
点4到根的路径上的个分别为{1, 2, 4}
点5到根的路径上的个分别为{1, 2, 5}
点6到根的路径上的个分别为{1, 3, 6}
点7到根的路径上的个分别为{1, 3, 7}
备注
设 \(n\) 为树的点数,保证树的编号为 \(1\)~\(n\) 的整数且互不相同
设 \(m\) 为问题个数
\(2 <= n <= 10^3\)
\(0 <= m <= 10^3\)
代码框预设代码
/*
* class ListNode {
* int val;
* ListNode next = null;
*
* public ListNode(int val) {
* this.val = val;
* }
* }
* /
/* class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
*
* public TreeNode(int val) {
* this.val = val;
* }
* }
*/
class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
* 你需要返回m个指针,第i个指针指向一条链,表示第i个问题的答案
*
* @param root TreeNode类 指向链表树的根
* @param b int整型一维数组 表示每个问题是什么
* @return ListNode类一维数组
*/
public ListNode[] solve(TreeNode root, int[] b) {
// write code here
}
}
二、数字变换
时间限制:C/C++ 1秒,其他语言 2秒
空间限制:C/C++ 262144K,其他语言 524288K
64bit IO Format: %lld
题目描述
现在有一个数字 \(n\) ,你可以通过下面三种变换,使得这个数字变成 \(0\) ,现在想知道最少需要变换几次
第一种变换:\(n = n - 1\)
第二种变换:若 \(n\) 是偶数,则 \(n = n / 2\)
第三种变换:若 \(n\) 是\(3\)的倍数,\(n = n / 3\).
本题为ACM模式,请通过代码实现题目,过程中的输入输出请自行处理,处理方式参考题目输入输出描述或左侧例题。
输入描述
输入第一行一个整数 \(T\) ,代表有 \(T\) 组测试数据
接下来 \(T\) 行,每一行为一个整数 \(n\) ,代表要变换的数。
\(1 <= T <= 100,1 <= n <= 2*10^9\)
输出描述
对于每组测试数据,输出一个答案代表最少需要变换的次数。
输入
1
10
输出
4
说明
先执行第一种变换变成 \(9\) ,执行第三种变换变成 \(3\),执行第三种变换变成 \(1\),最后执行第一种变换变成 \(0\)
三、小K的第K小元素
时间限制:C/C++ 1秒,其他语言 2秒
空间限制:C/C++ 262144K,其他语言 524288K
64bit IO Format: %lld
题目描述
小 \(K\) 有 \(n\) 个数组,并且他将数组标号为 \(1\)~\(n\) ,每个数组有若干个元素,现在他有 \(q\) 次询问,每次询问细节如下:
- 首先给出一个整数 \(P\) ,之后跟着 \(P\) 个互不相同的数组下标,最后给出一个整数 \(k\) 。
- 你需要告诉小 \(K\) ,将这 \(P\) 个数合并起来后的第 \(k\) 小元素是多少。
本题为ACM模式,请通过代码实现题目,过程中的输入输出请自行处理,处理方式参考题目输入输出描述或左侧例题。
输入描述
第一行包含一个正整数 \(n\) \((1<=n<=10^5)\),表示有 \(n\) 个数组。
接下来 \(n\) 行,每一行包含:
第一个数首先给出一个正整数 \(m_i\) \((1<=m_i<=10^5)\) ,表示第 \(i\) 个数组的长度。后面的 \(m_i\) 个正整数 \(a_{i,j}\) \((1<=a_{i,j}<=10^9)\) ,表示第 \(i\) 个数组的第 \(j\) 个元素。
第 \(n+2\) 行包含一个正整数 \(q\) \((1<=q<=10^5)\) ,表示询问的次数。
接下来 \(q\) 行,每一行包含:
首先给出一个正整数 \(p_i\) \((1<=p_i<=n)\) ,表示余姚合并的 \(p_i\) 个数组得个数。
接下来 \(p_i\) 个正整数, \(b_{i,j}\) \((a<=b_{i,j}<=n)\) ,表示第 \(i\) 次询问需要合并的第 \(j\) 个数组下标。
接下来给出一个正整数 \(k_i\) , \(k_i\) 比超过合并后数组的大小。
数据保证数组中元素总数小于等于 \(10^5\) ,询问中的数组下标总数小于等于 \(10^5\) 。
输出描述
对于每一次询问,都需要输出一行包含一个正整数,表示合并后的数组中的第 \(k\) 小元素。
输入1
2
1 2
2 1 3
2
1 1 1
2 1 2 2
输出1
2
2
说明1
第一行输入为 \(n\) ,代表 \(2\) 个数组
接了来 \(2\) 行表示有 \(2\) 个数组,分别为数组 \(1\) 和数组 \(2\) ,数组 \(1\) 的元素为 \(2\) ,数组 \(2\) 的元素为 \(1\) 和 \(3\)
接下来的 \(2\) 表示询问 \(2\) 次
询问第 \(1\) 次需要合并的数组个数为 \(1\) 个,也就是不需要合并,选中的数组为 \(1\) ,数组 \(1\) 只有 \(1\) 个元素,是 \(2\) ,第 \(1\) 小的元素也就是 \(2\) ,输出 \(2\)
询问第 \(2\) 次需要合并的数字个数为 \(2\) 个,需要合并,选中的数组为 \(1\) 和 \(2\) ,数组 \(1\) 和数组 \(2\) 合并之后为: \([2, 1, 3]\) ,第 \(2\) 小的元素也是 \(2\) ,输出 \(2\)
输入2
5
1 1
2 2 3
3 5 10 6
4 4 58 2 1
5 1000000000 9 8 4 5
5
1 2 2
2 2 3 3
3 3 4 5 11
4 5 4 3 2 1
5 1 2 5 4 3 7
输出2
3
5
58
1
4
说明2
第一次询问,只包含第二个数组,一共有 \(2\) 个数: \(2\) 和 \(3\) 。第 \(2\) 小的元素为 \(3\) 。
第三次询问,包含三个数组:第三、第四和第五,一共有 \(12\) 个数。其中第 \(11\) 小的元素为 \(58\) 。
四、奖金发放
时间限制:C/C++ 1秒,其他语言 2秒
空间限制:C/C++ 262144K,其他语言 524288K
64bit IO Format: %lld
题目描述
某公司年终共拿出 \(w\) 元,用于发放奖金(不需要用完)。公司共有 \(n\) 位员工(员工总数为奇数),每位员工贡献不同,发放奖金少于 \(x_i\) 元会让他自己不满意,多余 \(y_i\) 元会让其他员工不满意。现在想提出一种奖金发放的方案,使得所有人都满意,同时使得所有员工拿到奖金的中位数最大,求这个最大的中位数?
本题为ACM模式,请通过代码实现题目,过程中的输入输出请自行处理,处理方式参考题目输入输出描述或左侧例题。
输入描述
第一行两个正整数,员工数 \(n\) ,奖金总数 \(w\);接下来 \(n\) 行:
每行两个正整数 ,每个人的奖金下限 \(x_i\) 、奖金上限 \(y_i\) 。
输出描述
一个正整数,最大的奖金中位数。
输入
3 20
8 10
1 4
7 9
输出
9
说明
三人分别发放奖金 \(10\) 、\(1\) 、\(9\) 元,奖金中位数最大为 \(9\) 。
备注
\(1 <= n <= 10^5\)
\(1 <= w <= 10^14\)
\(1 <= x_i <= y_i <= 10^9\)
\(\sum^{}_{}{x_i} <= w <= \sum^{}_{}{y_i}\)
五、整数倍购物
时间限制:C/C++ 1秒,其他语言 2秒
空间限制:C/C++ 262144K,其他语言 524288K
64bit IO Format: %lld
题目描述
牛牛陪牛妹来到商场购物,许久没有逛商场的牛妹像发了疯似的挑选了起来。很快,牛妹挑选出了一共 \(n\) 件商品,为了方便区别,给其编号为 \(1, 2, …, n\) ,其中,第 \(i\) 件商品的价格为 \(w_i\)
牛牛一算总额,惊人地发现,这些东西太贵了,如果全部买下的话,自己的全部身家就没了。于是,牛牛找了个借口说道:“今天银行卡限额了,只能刷出整 \(m\) 倍数的金额,这些东西,可能……”
还没等牛牛说完,牛妹就明白了牛牛的意思,于是,准备从这 \(n\) 件商品中挑选若干件,使其总额恰好为 \(m\) 的整倍数。
牛牛在一旁盘算着,如果牛妹足够聪明,在满足 \(m\) 的整倍数的条件下,她会挑出最大的商品总金额。
所以请你告诉牛牛,最坏的情况下,这次购物之后,他的全部身家还能剩下多少。
本题为ACM模式,请通过代码实现题目,过程中的输入输出请自行处理,处理方式参考题目输入输出描述或左侧例题。
输入描述
第一行输入一个正整数 \(T\) \((1 <= T <= 10^5)\),代表测试数据的组数。
对于每组测试数据,第一次输入一个正整数 \(n, m\) (\(1 <= n <= 10^5\); \(1<= m <= 100\)) ,依次代表牛妹第一次挑出的商品数量,以及牛牛编造的整 \(m\) 倍数金额。
题目保证,所有测试数据的 \(n\) 之和不会超过 \(10^6\).
输出描述
对于每组测试数据,一行输出一个整数代表答案。
输入
2
3 3
3 6 9
3 5
9 6 3
输出
0
3
说明
第一组测试数据中,\(3 + 6 + 9 = 18\) ,是 \(3\) 的倍数,所以恰好花光牛牛的全部身家。
第二组测试数据中,要求总金额是 \(5\) 的备注,显然,对牛妹来说,最高花费的组合为 \(9 + 6 = 15\) ,此时,牛牛的全部身家还剩下 \(3\) .

