卷积神经网络：卷积层和池化层

Mnist是针对小图像块处理的，这篇讲的是针对大图像进行处理的。两者在这的区别还是很明显的，小图像（如8*8，MINIST的28*28）可以采用全连接的方式（即输入层和隐含层直接相连）。但是大图像，这个将会变得很耗时：比如96*96的图像，若采用全连接方式，需要96*96个输入单元，然后如果要训练100个特征，只这一层就需要96*96*100个参数（W,b），训练时间将是前面的几百或者上万倍。所以这里用到了部分联通网络。对于图像来说，每个隐含单元仅仅连接输入图像的一小片相邻区域。

 

卷积层：

　　自然图像有其固有特性，也就是说，图像的一部分的统计特性与其他部分是一样的。这也意味着我们在这一部分学习的特征也能用在另一部分上，所以对于这个图像上的所有位置，我们都能使用同样的学习特征。

　　对于图像，当从一个大尺寸图像中随机选取一小块，比如说8x8作为样本，并且从这个小块样本中学习到了一些特征，这时我们可以把从这个8x8样本中学习到的特征作为探测器，应用到这个图像的任意地方中去。特别是，我们可以用从8x8样本中所学习到的特征跟原本的大尺寸图像作卷积，从而对这个大尺寸图像上的任一位置获得一个不同特征的激活值。

　　看下面例子容易理解：

　　假设你已经从一个96x96的图像中学习到了它的一个8x8的样本所具有的特征，假设这是由有100个隐含单元的自编码完成的。为了得到卷积特征，需要对96x96的图像的每个8x8的小块图像区域都进行卷积运算。也就是说，抽取8x8的小块区域，并且从起始坐标开始依次标记为（1，1），（1，2），...，一直到（89，89），然后对抽取的区域逐个运行训练过的稀疏自编码来得到特征的激活值。在这个例子里，显然可以得到100个集合，每个集合含有89x89个卷积特征。

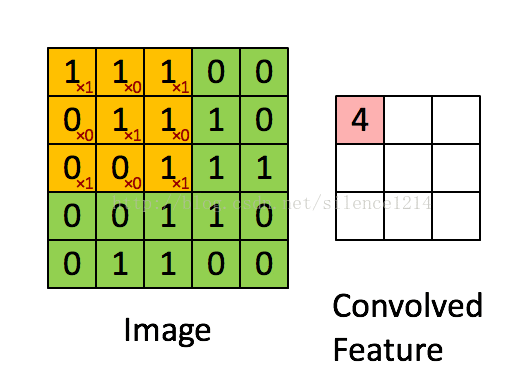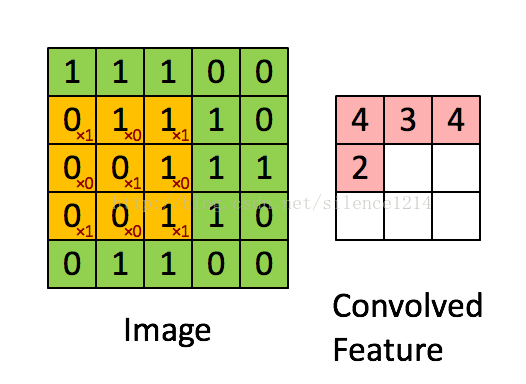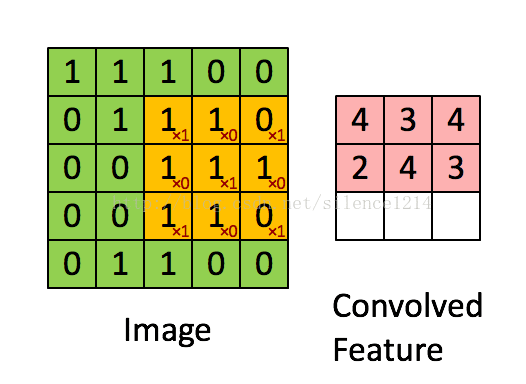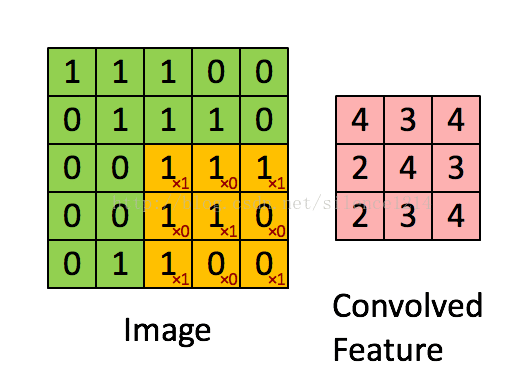
最后，总结下convolution的处理过程：

　　假设给定了r * c的大尺寸图像，将其定义为xlarge。首先通过从大尺寸图像中抽取的a * b的小尺寸图像样本xsmall训练稀疏自编码，得到了k个特征（k为隐含层神经元数量），然后对于xlarge中的每个a*b大小的块，求激活值fs，然后对这些fs进行卷积。这样得到（r-a+1）*（c-b+1）*k个卷积后的特征矩阵。

 

池化层：

　　在通过卷积获得了特征（features）之后，下一步我们希望利用这些特征去做分类。理论上讲，人们可以把所有解析出来的特征关联到一个分类器，例如softmax分类器，但计算量非常大。例如：对于一个96X96像素的图像，假设我们已经通过8X8个输入学习得到了400个特征。而每一个卷积都会得到一个(96 − 8 + 1) * (96 − 8 + 1) = 7921的结果集，由于已经得到了400个特征，所以对于每个样例（example）结果集的大小就将达到892 * 400 = 3,168,400 个特征。这样学习一个拥有超过3百万特征的输入的分类器是相当不明智的，并且极易出现过度拟合（over-fitting）.

　　所以就有了pooling这个方法，翻译作“池化”？感觉pooling这个英语单词还是挺形象的，翻译“作池”化就没那么形象了。其实也就是把特征图像区域的一部分求个均值或者最大值，用来代表这部分区域。如果是求均值就是mean pooling，求最大值就是max pooling。

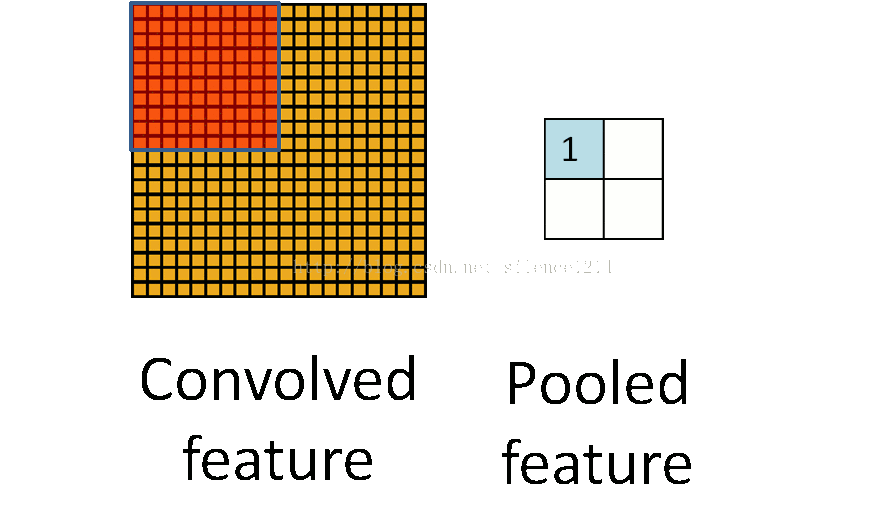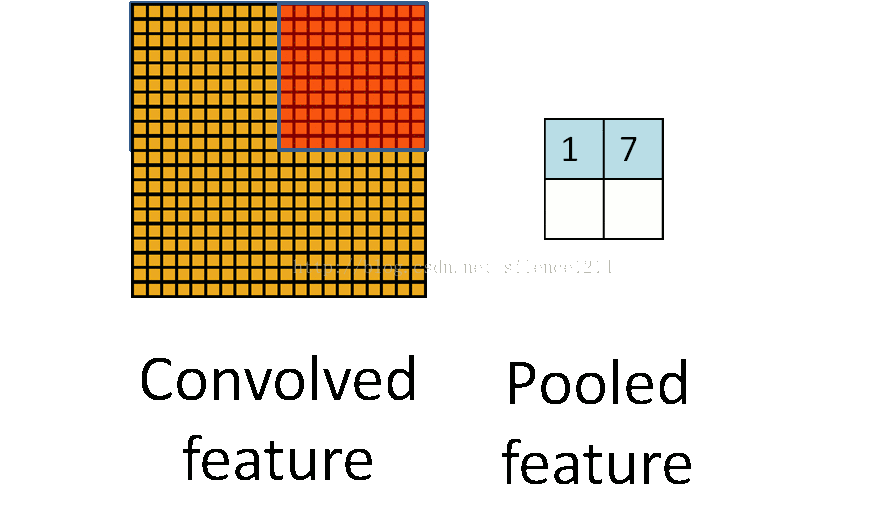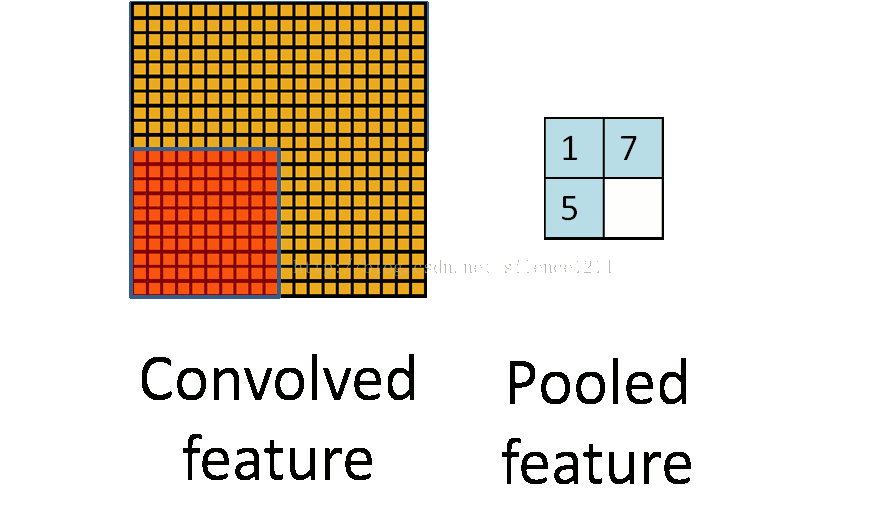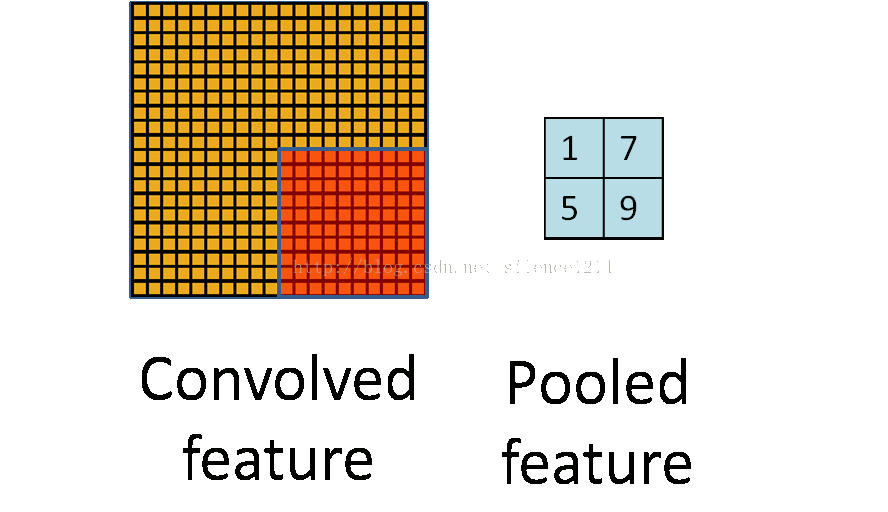
　　至于pooling为什么可以这样做，是因为：我们之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性，这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此，为了描述大的图像，一个很自然的想法就是对不同位置的特征进行聚合统计。这个均值或者最大值就是一种聚合统计的方法。

　　另外，如果人们选择图像中的连续范围作为池化区域，并且只是池化相同(重复)的隐藏单元产生的特征，那么，这些池化单元就具有平移不变性(translation invariant)。这就意味着即使图像经历了一个小的平移之后，依然会产生相同的（池化的）特征（这里有个小小的疑问，既然这样，是不是只能保证在池化大小的这块区域内具有平移不变性？）。在很多任务中（例如物体检测、声音识别），我们都更希望得到具有平移不变性的特征，因为即使图像经过了平移，样例（图像）的标记仍然保持不变。例如，如果你处理一个MNIST数据集的数字，把它向左侧或右侧平移，那么不论最终的位置在哪里，你都会期望你的分类器仍然能够精确地将其分类为相同的数字。