二叉树的遍历算法（递归、层次、非递归）(c++)

二叉树的遍历算法（递归、层次、非递归）

递归、层次遍历算法

先序遍历

• 若二叉树为空，遍历结束；否则，先根结点、再左子树、后右子树

/*
//二叉链表结点定义
template <class T>
class BiTreeNode
{
public:
	T data;	//数据域
	BiTreeNode<T>* lchild;	//左孩子指针域
	BiTreeNode<T>* rchild;	//右孩子指针域
};
*/

template<typename T>
void BiTree<T>::PreOrder(BiTreeNode<T>* bt)
{
	if (bt == NULL)		//递归调用的结束条件
	{
		return;
	}
	cout << bt->data;	//访问根结点bt的数据域
	PreOrder(bt->lchild);	//先序递归遍历bt的左子树
	PreOrder(bt->rchild);	//先序遍历bt的右子树
}

中序遍历

• 若二叉树为空，遍历结束；否则，先左子树、再根结点、后右子树

/*
//二叉链表结点定义
template <class T>
class BiTreeNode
{
public:
	T data;	//数据域
	BiTreeNode<T>* lchild;	//左孩子指针域
	BiTreeNode<T>* rchild;	//右孩子指针域
};
*/

template<typename T>
void BiTree<T>::InOrder(BiTreeNode<T>* bt)
{
	if (bt == NULL)
	{
		return;
	}
	InOrder(bt->lchild);
	cout << bt->data;
	InOrder(bt->rchild);
}

后序遍历

• 若二叉树为空，遍历结束；否则，先左子树、再右子树、后根结点

/*
//二叉链表结点定义
template <class T>
class BiTreeNode
{
public:
	T data;	//数据域
	BiTreeNode<T>* lchild;	//左孩子指针域
	BiTreeNode<T>* rchild;	//右孩子指针域
};
*/

template<typename T>
void BiTree<T>::PostOrder(BiTreeNode<T>* bt)
{
	if (bt == NULL)
	{
		return;
	}
	PostOrder(bt->lchild);
	PostOrder(bt->rchild);
	cout << bt->data;
}

层次遍历

• 二叉树的层次遍历是指从二叉树的根结点开始，从上往下、从左往右逐层遍历，对一层结点访问完以后，再按照它们的访问次序依次访问各个结点的左、右孩子，这样一层一层地进行，先遇到的结点先访问，符合队列操作规则。

• 首先将根结点入队，然后从队头取一个元素，每取一个元素，执行如下3个动作：

  1. 访问该元素所指结点
  2. 如果该元素所指结点有左孩子，则左孩子指针入队
  3. 如果该元素所指结点右有孩子，则右孩子指针入队

  重复以上操作，知道队列为空

• 算法具体实现代码

/*
//所需队列定义
const int QUEUE_MAX_SIZE = 100;	//默认队列大小为100
template <class T>
class Queue
{
public:
	T data[QUEUE_MAX_SIZE];
	int front, rear;
};

//二叉链表结点定义
template <class T>
class BiTreeNode
{
public:
	T data;	//数据域
	BiTreeNode<T>* lchild;	//左孩子指针
	BiTreeNode<T>* rchild;	//右孩子指针
};
*/

template<typename T>
void BiTree<T>::LevelOrder(BiTreeNode<T>* bt)
{
	if (bt == NULL)
	{
		return;	//空树
	}
	Queue<BiTreeNode<T>*> Q;
	Q.front = Q.rear = -1;
	Q.data[++Q.rear] = root;
	while (Q.rear != Q.front)
	{
		BiTreeNode<T>* q = Q.data[++Q.front];	//出队
		cout << q->data;
		if (q->lchild != NULL)	//左孩子入队
		{
			Q.data[++Q.rear] = q->lchild;
		}
		if (q->rchild != NULL)	//右孩子入队
		{
			Q.data[++Q.rear] = q->rchild;
		}
	}
}

完整代码（c++）

#pragma once
#include <iostream>

using namespace std;

//层次遍历所需队列定义
const int QUEUE_MAX_SIZE = 100;	//默认队列大小为100
template <class T>
class Queue
{
public:
	T data[QUEUE_MAX_SIZE];
	int front, rear;
};

//二叉链表结点定义
template <class T>
class BiTreeNode
{
public:
	T data;	//数据域
	BiTreeNode<T>* lchild;	//左孩子指针
	BiTreeNode<T>* rchild;	//右孩子指针
};

//二叉链表类实现
template <class T>
class BiTree
{
private:
	BiTreeNode<T>* root;					//指向根结点的头结点
	BiTreeNode<T>* Creat(BiTreeNode<T>* bt);//构造函数调用
	void Release(BiTreeNode<T>* bt);		//析构函数调用
	void PreOrder(BiTreeNode<T>* bt);		//DLR
	void InOrder(BiTreeNode<T>* bt);		//LDR
	void PostOrder(BiTreeNode<T>* bt);		//LRD
	void LevelOrder(BiTreeNode<T>* bt);		//层次遍历	
public:
	BiTree() { root = Creat(root); };		//构造函数  构建一棵二叉树
	~BiTree() { Release(root); };			//析构函数	释放个结点的空间
	void PreOrder() { PreOrder(root); };	//DLR
	void InOrder() { InOrder(root); };		//LDR
	void PostOrder() { PostOrder(root); };	//LDR
	void LeverOrder() { LevelOrder(root); };//层次遍历
};

template <typename T>
BiTreeNode<T>* BiTree<T>::Creat(BiTreeNode<T>* bt)
{
	T ch;
	cin >> ch;	//输入结点的数据信息  假定为字符
	if (ch == '#')
	{
		bt = NULL;	//建立一棵空树
	}
	else
	{
		bt = new BiTreeNode<T>;	//生成一个结点，数据域为ch
		bt->data = ch;
		bt->lchild = Creat(bt->lchild);	//递归建立左子树
		bt->rchild = Creat(bt->rchild);	//递归建立右子树
	}
	return bt;
}

template<typename T>
void BiTree<T>::Release(BiTreeNode<T>* bt)
{
	if (bt != NULL)
	{
		Release(bt->lchild);	//释放左子树
		Release(bt->rchild);	//释放右子树
		delete bt;	//释放根结点
	}
}

template<typename T>
void BiTree<T>::PreOrder(BiTreeNode<T>* bt)
{
	if (bt == NULL)		//递归调用的结束条件
	{
		return;
	}
	cout << bt->data;	//访问根结点bt的数据域
	PreOrder(bt->lchild);	//先序递归遍历bt的左子树
	PreOrder(bt->rchild);	//先序遍历bt的右子树
}

template<typename T>
void BiTree<T>::InOrder(BiTreeNode<T>* bt)
{
	if (bt == NULL)
	{
		return;
	}
	InOrder(bt->lchild);
	cout << bt->data;
	InOrder(bt->rchild);
}

template<typename T>
void BiTree<T>::PostOrder(BiTreeNode<T>* bt)
{
	if (bt == NULL)
	{
		return;
	}
	PostOrder(bt->lchild);
	PostOrder(bt->rchild);
	cout << bt->data;
}
template<typename T>
void BiTree<T>::LevelOrder(BiTreeNode<T>* bt)
{
	if (bt == NULL)
	{
		return;	//空树
	}
	Queue<BiTreeNode<T>*> Q;
	Q.front = Q.rear = -1;
	Q.data[++Q.rear] = root;
	while (Q.rear != Q.front)
	{
		BiTreeNode<T>* q = Q.data[++Q.front];	//出队
		cout << q->data;
		if (q->lchild != NULL)	//左孩子入队
		{
			Q.data[++Q.rear] = q->lchild;
		}
		if (q->rchild != NULL)	//右孩子入队
		{
			Q.data[++Q.rear] = q->rchild;
		}
	}
}

int main()
{
    cout << "请按先序输入二叉树的各个结点（空用#符号表示）：" << endl;
	BiTree<char>* bitree = new BiTree<char>();	//创建一棵二叉树
    
	cout << "先序遍历如下：" << endl;
	bitree->PreOrder();
	cout << endl;

	cout << "中序遍历如下：" << endl;
	bitree->InOrder();
	cout << endl;

	cout << "后序遍历如下：" << endl;
	bitree->PostOrder();
	cout << endl;

	cout << "层次遍历如下：" << endl;
	bitree->LeverOrder();
	cout << endl;

	system("pause");

	return 0;
}

• 输出
  

非递归遍历算法

算法思想

• 从根结点开始沿左子树深入下去，当到达左子树最左端时，返回；当返回的结点存在右子树，进入该结点右子树，再进行如此深入和返回，直到最后从根结点的右子树返回到根结点

• 遍历路程图（ △ 表示先序遍历路线，* 表示中序遍历路线，★表示后序遍历路线）
  

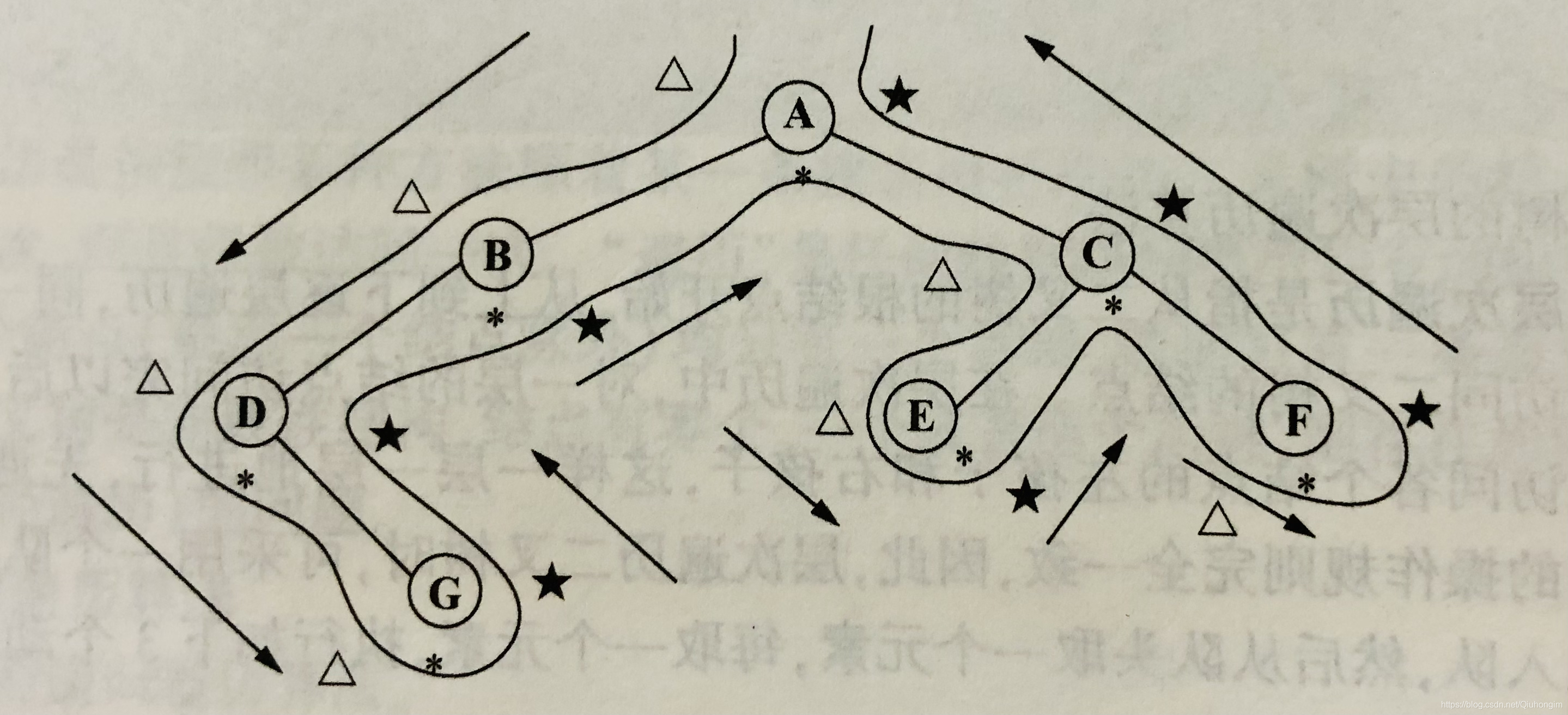
  先序遍历：结点第一次遇到时访问结点

  中序遍历：结点第二次遇到时访问结点（从左子树返回后访问）

  后序遍历：结点第三次遇到时访问结点（从右子树返回后访问）

算法实现所需的数据类型—栈

• 在不断深入返回过程中，先深入的后返回，符合栈的特征

先序遍历

算法策略

• 从根结点沿左子树深入，每深入一个结点，就入栈并访问一个，当到达最左端时，返回，当结点返回时出栈，然后从该结点右子树继续深入，如此进行下去，直到从根结点的右子树返回

遍历算法（c++）

/*
const int MAXNODE = 10;	//默认二叉树最大结点为10
//二叉链表结点定义
template <class T>
class BiTreeNode
{
public:
	T data;				//数据域
	BiTreeNode* lchild;	//左孩子指针域
	BiTreeNode* rchild;	//右孩子指针域
};
*/

/*先序遍历（非递归）*/
template <typename T>
void BiTree<T>::PreOrder(BiTreeNode<T>* bt)
{
	BiTreeNode<T>* s[MAXNODE];	//定义栈S  用于暂时存储二叉树结点
	BiTreeNode<T>* p = bt;
	int top = -1;
	if (bt == NULL)
	{
		return;	//空树
	}
	while (!(p == NULL && top == -1))
	{
		while (p != NULL)
		{
			if (top < MAXNODE - 1)
			{
				++top;
				s[top] = p;
			}
			else
			{
				cout << "Stack OverFlow!" << endl;
			}
			cout << p->data;	//访问结点数据域
			p = p->lchild;
		}
		if (top == -1)
		{
			return;	//栈空结束
		}
		else
		{
			p = s[top];	//弹出栈顶元素
			--top;
			p = p->rchild;
		}
	}
}

中序遍历

算法策略

• 从根结点沿左子树深入，每深入一个结点，就入栈一个，当到达最左端时，返回，当结点返回时出栈并访问，然后从该结点右子树继续深入，如此进行下去，直到从根结点的右子树返回

遍历算法（c++）

/*
const int MAXNODE = 10;	//默认二叉树最大结点为10
//二叉链表结点定义
template <class T>
class BiTreeNode
{
public:
	T data;				//数据域
	BiTreeNode* lchild;	//左孩子指针域
	BiTreeNode* rchild;	//右孩子指针域
};
*/

/*中序遍历（非递归）*/
template <typename T>
void BiTree<T>::InOrder(BiTreeNode<T>* bt)
{
	BiTreeNode<T>* s[MAXNODE];	//定义栈S  用于暂时存储二叉树结点
	BiTreeNode<T>* p = bt;
	int top = -1;	
	if (bt == NULL)
	{
		return;	//空树
	}
	while (!(p == NULL && top == -1))
	{
		while (p != NULL)
		{
			if (top < MAXNODE - 1)
			{
				++top;
				s[top] = p;
			}
			else
			{
				cout << "Stack OverFlow!" << endl;
			}
			p = p->lchild;
		}
		if (top == -1)
		{
			return;	//栈空结束
		}
		else
		{
			p = s[top];	//弹出栈顶元素
			--top;
			cout << p->data;	//访问结点数据域
			p = p->rchild;
		}
	}
}

后序遍历

算法策略

• 由于后序遍历是从右子树返回时才访问结点，因此存在两种情况
  1. 结点没有右孩子
  2. 结点有右孩子
• 因此我们需要一个辅助指针用于标记结点是从左子树返回还是右子树返回，当结点属于情况一，直接弹出并访问，修改辅助指针指向该结点，之后继续访问栈顶元素，当栈顶元素属于情况二，入栈，继续深入该结点左子树并入栈，如此进行下去，每弹出一个结点，都修改辅助指针指向该结点。

遍历算法（c++）

/*
const int MAXNODE = 10;	//默认二叉树最大结点为10
//二叉链表结点定义
template <class T>
class BiTreeNode
{
public:
	T data;				//数据域
	BiTreeNode* lchild;	//左孩子指针域
	BiTreeNode* rchild;	//右孩子指针域
};
*/

/*后序遍历（非递归）*/
template <typename T>
void BiTree<T>::PostOrder(BiTreeNode<T>* bt)
{
	BiTreeNode<T>* s[MAXNODE];	//定义栈S  用于暂时存储二叉树结点
	BiTreeNode<T>* p = bt;
	BiTreeNode<T>* r = NULL;	//辅助指针,用于标记是从左或右子树返回
	int top = -1;
	if (bt == NULL)
	{
		return;	//空树
	}
	while (!(p == NULL && top == -1))	//栈非空且二叉树非空
	{
		while (p != NULL)	
		{
			if (top < MAXNODE - 1)
			{
				++top;
				s[top] = p;
			}
			else
			{
				cout << "Stack OverFlow!" << endl;
			}
			p = p->lchild;
		}
		if (top == -1)
		{
			return;	//栈空结束
		}
		else
		{
			p = s[top];
			if (p->rchild && p->rchild != r)	//存在右子树，并且未被访问过
			{
				p = p->rchild;
				++top;
				s[top] = p;
				p = p->lchild;
			}
			else								//不存在右子树或已经访问完了
			{
				--top;
				cout << p->data;
				r = p;
				p = NULL;
			}
		}
	}
}

完整代码（c++）

#pragma once
#include <iostream>

const int MAXNODE = 10;	//默认二叉树最大结点为10

using namespace std;

/*二叉链表结点定义*/
template <class T>
class BiTreeNode
{
public:
	T data;				//数据域
	BiTreeNode* lchild;	//左孩子指针域
	BiTreeNode* rchild;	//右孩子指针域
};

/*二叉链表类实现*/
template <class T>
class BiTree
{
public:
	BiTree() { root = PreCreate(root); };			//构造函数
	~BiTree() { Release(root); };					//析构函数
	void PreOrder() { PreOrder(root); };			//DLR
	void InOrder() { InOrder(root); };				//LDR
	void PostOrder() { PostOrder(root); };			//LRD
private:
	BiTreeNode<T>* root;							//二叉树根结点
	BiTreeNode<T>* PreCreate(BiTreeNode<T>* bt);	//先序创建二叉树（递归）
	void Release(BiTreeNode<T>* bt);				//释放结点（递归）
	void PreOrder(BiTreeNode<T>* bt);				//先序遍历（非递归）
	void InOrder(BiTreeNode<T>* bt);				//中序遍历（非递归）
	void PostOrder(BiTreeNode<T>* bt);				//后序遍历（非递归）
};

/*先序创建二叉树（递归）*/
template <typename T>
BiTreeNode<T>* BiTree<T>::PreCreate(BiTreeNode<T>* bt)
{
	T ch;
	cin >> ch;
	if (ch == '#')
	{
		bt = NULL;
	}
	else
	{
		bt = new BiTreeNode<T>;
		bt->data = ch;
		bt->lchild = PreCreate(bt->lchild);
		bt->rchild = PreCreate(bt->rchild);
	}
	return bt;
}

/*释放结点（递归）*/
template <typename T>
void BiTree<T>::Release(BiTreeNode<T>* bt)
{
	if (bt != NULL)
	{
		Release(bt->lchild);
		Release(bt->rchild);
		delete bt;
	}
}

/*先序遍历（非递归）*/
template <typename T>
void BiTree<T>::PreOrder(BiTreeNode<T>* bt)
{
	BiTreeNode<T>* s[MAXNODE];	//定义栈S  用于暂时存储二叉树结点
	BiTreeNode<T>* p = bt;
	int top = -1;
	if (bt == NULL)
	{
		return;	//空树
	}
	while (!(p == NULL && top == -1))
	{
		while (p != NULL)
		{
			if (top < MAXNODE - 1)
			{
				top++;
				s[top] = p;
			}
			else
			{
				cout << "Stack OverFlow!" << endl;
			}
			cout << p->data;	//访问结点数据域
			p = p->lchild;
		}
		if (top == -1)
		{
			return;	//栈空结束
		}
		else
		{
			p = s[top];	//弹出栈顶元素
			--top;
			p = p->rchild;
		}
	}
}
/*中序遍历（非递归）*/
template <typename T>
void BiTree<T>::InOrder(BiTreeNode<T>* bt)
{
	BiTreeNode<T>* s[MAXNODE];	//定义栈S  用于暂时存储二叉树结点
	BiTreeNode<T>* p = bt;
	int top = -1;	
	if (bt == NULL)
	{
		return;	//空树
	}
	while (!(p == NULL && top == -1))
	{
		while (p != NULL)
		{
			if (top < MAXNODE - 1)
			{
				top++;
				s[top] = p;
			}
			else
			{
				cout << "Stack OverFlow!" << endl;
			}
			p = p->lchild;
		}
		if (top == -1)
		{
			return;	//栈空结束
		}
		else
		{
			p = s[top];	//弹出栈顶元素
			--top;
			cout << p->data;	//访问结点数据域
			p = p->rchild;
		}
	}
}

/*后序遍历（非递归）*/
template <typename T>
void BiTree<T>::PostOrder(BiTreeNode<T>* bt)
{
	BiTreeNode<T>* s[MAXNODE];	//定义栈S  用于暂时存储二叉树结点
	BiTreeNode<T>* p = bt;
	BiTreeNode<T>* r = NULL;	//辅助指针,用于标记是从左或右子树返回
	int top = -1;
	if (bt == NULL)
	{
		return;	//空树
	}
	while (!(p == NULL && top == -1))	//栈非空且二叉树非空
	{
		while (p != NULL)	//
		{
			if (top < MAXNODE - 1)
			{
				top++;
				s[top] = p;
			}
			else
			{
				cout << "Stack OverFlow!" << endl;
			}
			p = p->lchild;
		}
		if (top == -1)
		{
			return;	//栈空结束
		}
		else
		{
			p = s[top];
			if (p->rchild && p->rchild != r)
			{
				p = p->rchild;
				top++;
				s[top] = p;
				p = p->lchild;
			}
			else
			{
				--top;
				cout << p->data;
				r = p;
				p = NULL;
			}
		}
	}
}

int main()
{
	cout << "请按先序遍历输入二叉树（空节点用#表示）：" << endl;
	BiTree<char>* bitree = new BiTree<char>();

	cout << "先序遍历（非递归）如下：" << endl;
	bitree->PreOrder();
	cout << endl;

	cout << "中序遍历（非递归）如下：" << endl;
	bitree->InOrder();
	cout << endl;

	cout << "后序遍历（非递归）如下：" << endl;
	bitree->PostOrder();
	cout << endl;

	system("pause");

	return 0;
}

• 输出