二叉排序树结点的查找、插入、删除
二叉排序树（查找、结点增加、删除）
定义
-
或是空树
-
或具有下列性质：
- 若左子树不为空，则左子树上所有结点的值均小于根结点的值
- 若右子树不为空，则右子树上所有结点的值均大于根结点的值
- 左右子树本身也是一棵二叉排序树
-
举例：
优点
- 提高查找和插入删除关键字的速度
结点查找
算法分析
-
若二叉排序树为空，查找失败
-
若二叉排序树非空，比较查找关键字，若相等，查找成功，否则：
A.若关键字小于根结点的关键字值，在根结点的左子树上继续查找，转向1
B.若关键字大于根结点的关键字值，在根结点的右子树上继续查找，转向1
代码实现
bool BiTree::Search(BiNode* bt, char key)
{
if (bt == NULL)
{
return false;
}
else
{
if (bt->data == key)
{
return true;
}
else if (key < bt->data)
{
return Search(bt->lchild, key);
}
else
{
return Search(bt->rchild, key);
}
}
}
改进后查找算法
- 改进背景：因为二叉排序树通常不是一次生成的，而是在查找过程中，当树中不存在关键字等于给定值结点时，通过将新结点陆续插入形成的。
- 算法修改地方：当查找失败，记录查找路径上访问的最后一个结点。
/*
bt 指向二叉排序树根结点的指针
key 查找关键字
q 指向结点的指针的指针 若查找成功，指针q指向该结点 否则，指针q指向查找路径上最后一个访问结点
q使用双重指针，而不是指针变量的目的，为了使q在函数结束后不会消失，因为q记录了最后一个结点的位置，而这个变量我在后边的插入结点需要用到，
所以我用了双重指针，使得q在后边的插入结点操作与传入的q使用了同一块内存
p 指向结点的双亲的指针 初始时为NULL
*/
bool BiTree::Search(BiNode* bt, char key, BiNode** p, BiNode** q)
{
if (!bt)
{
*q = p;
return false; //查找失败
}
else
{
if (bt->data == key)
{
*q = bt;
return true;
}
else if (key < bt->data)
{
return Search(bt->lchild, key, bt, q);
}
else
{
return Search(bt->rchild, key, bt, q);
}
}
}
结点插入
-
在查找过程中，若树不存在该关键字，则插入结点
-
新插入的结点一定是一个新添加的叶子结点，并且是查找失败时查找路径上访问的最后一个结点的左孩子或右孩子
算法分析
-
在二叉排序树中查找给定值的结点，若查找成功，则返回true，否则，返回false，并按以下步骤插入结点：
-
如果查找路径访问的最后一个结点为空，表示空树，则将给定值的结点作为该二叉树的根结点
-
如果查找路径访问的最后一个结点非空，若给定值小于该结点，则将给定值作为该结点左孩子插入，否则，作为右孩子插入
-
代码实现
bool BiTree::Insert(BiNode** bt, char key)
{
BiNode* s = NULL;
BiNode* q = NULL;
if (!Search(*bt, key, NULL, &q)) //查找失败
{
s = new BiNode;
s->data = key;
if (!q)
{
*bt = s;
s->lchild = NULL;
s->rchild = NULL;
}
else if (key < q->data) //s作为左孩子结点插入
{
q->lchild = s;
s->lchild = NULL;
s->rchild = NULL;
}
else //s作为右孩子插入
{
q->rchild = s;
s->lchild = NULL;
s->rchild = NULL;
}
return true;
}
else//查找成功
{
return false; //插入失败
}
}
结点删除
-
情况一： 仅有根结点
-
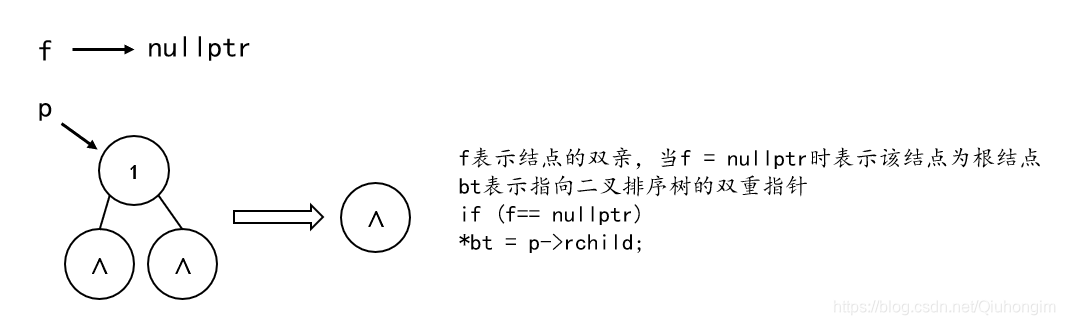
情况二：删除结点为叶子结点
-
情况三：删除结点只有左子树或只有右子树
-
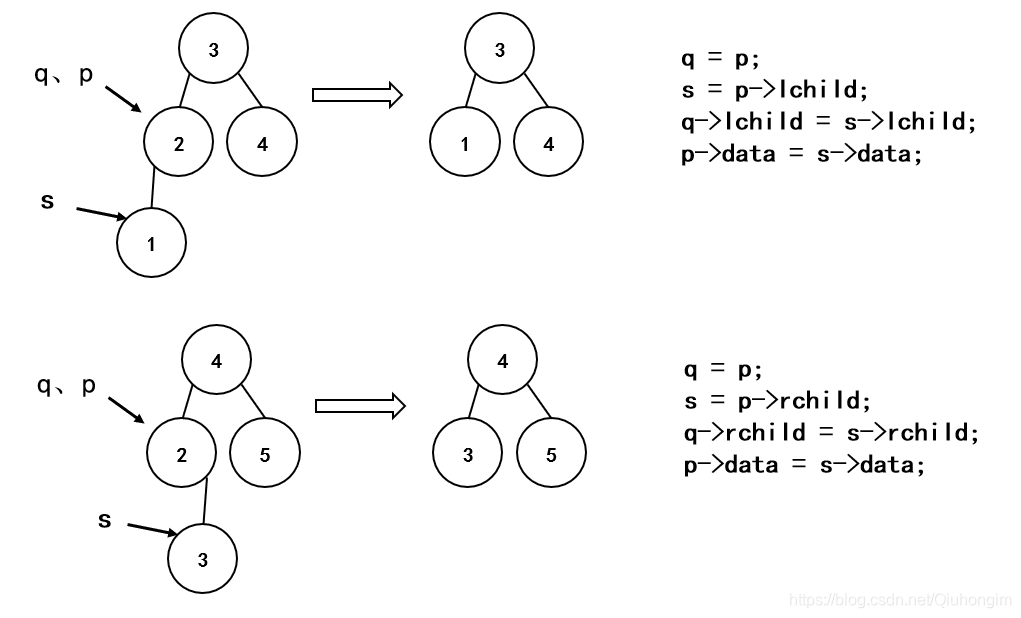
情况四：删除结点既有左子树又有右子树
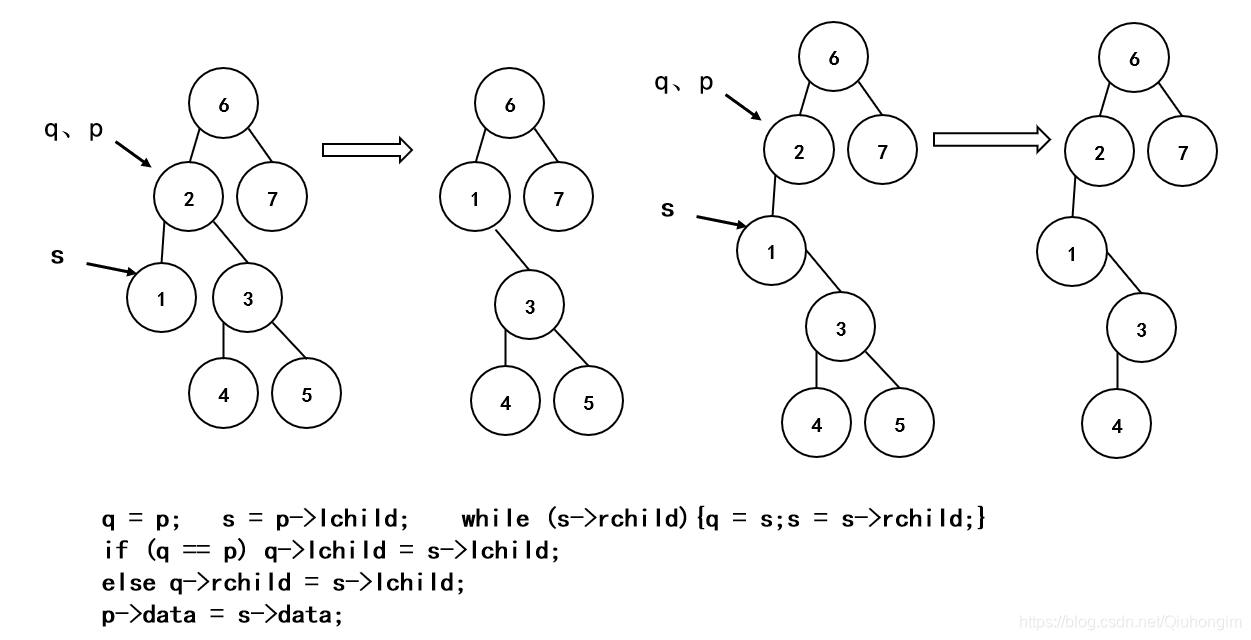
代码实现
bool BiTree::Delete(BiNode** bt, char key)
{
BiNode* p, * f, * s, * q;
p = *bt;
f = nullptr;
while (p && p->data != key)
{
f = p;
if (p->data > key) p = p->lchild;
else p = p->rchild;
}
if (p == nullptr) return false;
if (p->lchild == nullptr)
{
if (f == nullptr) *bt = p->rchild;
else if (f->lchild == p) f->lchild = p->rchild;
else f->rchild = p->rchild;
delete p;
return true;
}
else
{
q = p;
s = p->lchild;
while (s->rchild)
{
q = s;
s = s->rchild;
}
if (q == p) q->lchild = s->lchild;
else q->rchild = s->lchild;
p->data = s->data;
delete s;
return true;
}
}
完整代码
#pragma once
#include <iostream>
using namespace std;
/*二叉树结点定义*/
class BiNode
{
public:
char data; //数据域
BiNode* lchild; //左孩子指针域
BiNode* rchild; //右孩子指针域
};
/*二叉树类实现*/
class BiTree
{
public:
BiTree() { root = Create(root); }; //构造函数
~BiTree() { Release(root); }; //析构函数
void PreOrder() { PreOrder(root); }; //先序遍历（递归）
void Search(char key); //查找
void Insert(char key) { Insert(root,key); };
void Delete(char key) { Delete(&root, key); };
private:
BiNode* root; //根结点
BiNode* Create(BiNode* bt); //二叉树创建
void Release(BiNode* bt); //delete所有new出来的结点
void PreOrder(BiNode* bt); //先序遍历（递归）
bool Search(BiNode* bt, char key); //查找
bool Search(BiNode* bt, char key, BiNode* p, BiNode** q);//改进后的查找算法
bool Insert(BiNode* bt, char key); //插入算法
bool Delete(BiNode** bt, char key); //删除结点
};
/*递归先序创建二叉树*/
BiNode* BiTree::Create(BiNode* bt)
{
char ch;
cin >> ch;
if (ch == '#')
{
bt = NULL;
}
else
{
bt = new BiNode;
bt->data = ch;
bt->lchild = Create(bt->lchild);
bt->rchild = Create(bt->rchild);
}
return bt;
}
/*delete堆区new出来的结点*/
void BiTree::Release(BiNode* bt)
{
if (bt == NULL)
{
return;
}
else
{
Release(bt->lchild);
Release(bt->rchild);
delete bt;
}
}
/*先序遍历（递归）*/
void BiTree::PreOrder(BiNode* bt)
{
if (bt == nullptr)
{
return; //空树返回
}
else
{
cout << bt->data;
PreOrder(bt->lchild);
PreOrder(bt->rchild);
}
}
/*查找*/
bool BiTree::Search(BiNode* bt, char key)
{
if (bt == NULL)
{
return false;
}
else
{
if (bt->data == key)
{
return true;
}
else if (key < bt->data)
{
return Search(bt->lchild, key);
}
else
{
return Search(bt->rchild, key);
}
}
}
void BiTree::Search(char key)
{
bool flag = Search(root, key);
if (flag)
{
cout << "查找成功！" << endl;
}
else
{
cout << "查找失败！" << endl;
}
}
/*改进的查找算法*/
bool BiTree::Search(BiNode* bt, char key, BiNode* p, BiNode** q)
{
/*
* 在根指针bt所指的二叉排序树中递归查找关键字等于key的结点，若查找成功，指针q指向该结点，并返回true
* 否则，指针q指向查找路径上最后一个访问结点，并返回false，指针p指向bt双亲,初始调用值为NULL
*/
if (!bt)
{
*q = p;
return false; //查找失败
}
else
{
if (bt->data == key)
{
*q = bt;
return true;
}
else if (key < bt->data)
{
return Search(bt->lchild, key, bt, q);
}
else
{
return Search(bt->rchild, key, bt, q);
}
}
}
bool BiTree::Insert(BiNode* bt, char key)
{
BiNode* s = nullptr;
BiNode* q = nullptr;
if (!Search(bt, key, nullptr, &q)) //查找失败
{
s = new BiNode;
s->data = key;
if (!q)
{
bt = s;
s->lchild = nullptr;
s->rchild = nullptr;
}
else if (key < q->data) //s作为左孩子结点插入
{
q->lchild = s;
s->lchild = nullptr;
s->rchild = nullptr;
}
else //s作为右孩子插入
{
q->rchild = s;
s->lchild = nullptr;
s->rchild = nullptr;
}
return true;
}
else//查找成功
{
return false; //插入失败
}
}
bool BiTree::Delete(BiNode** bt, char key)
{
BiNode* p, * f, * s, * q;
p = *bt;
f = nullptr;
while (p && p->data != key)
{
f = p;
if (p->data > key) p = p->lchild;
else p = p->rchild;
}
if (p == nullptr) return false;
if (p->lchild == nullptr)
{
if (f == nullptr) *bt = p->rchild;
else if (f->lchild == p) f->lchild = p->rchild;
else f->rchild = p->rchild;
delete p;
return true;
}
else
{
q = p;
s = p->lchild;
while (s->rchild)
{
q = s;
s = s->rchild;
}
if (q == p) q->lchild = s->lchild;
else q->rchild = s->lchild;
p->data = s->data;
delete s;
return true;
}
}
int main()
{
cout << "请按先序遍历创建二叉排序树：" << endl;
BiTree* bt = new BiTree();
cout << "二叉排序树创建完毕！" << endl;
cout << "二叉排序树中序遍历序列如下：" << endl;
bt->PreOrder();
cout << endl;
cout << "请输入你要查找的值：" << endl;
char key1;
cin >> key1;
bt->Search(key1);
cout << "请输入你要插入的值：" << endl;
char key2;
cin >> key2;
bt->Insert(key2);
cout << "插入完成！" << endl;
cout << "请输入你要删除的值：" << endl;
char key3;
cin >> key3;
bt->Delete(key3);
cout << "删除完成！" << endl;
cout << "删除后前序遍历二叉排序树：" << endl;
bt->PreOrder();
cout << endl;
system("pause");
return 0;
}
