平衡二叉树
平衡二叉树(AVL树)
定义
- 或是空树
- 或是每个结点深度之差不超过1的二叉排序树
- 举例如下(结点的平衡因子=左子树深度-右子树深度):

旋转(将二叉排序树调整为二叉平衡树)
- 由于在二叉平衡树中插入或删除结点后,可能使平衡二叉树失去平衡,因此需要对其进行调整。
- 假设结点a是失去平衡的最小子树的根结点
1. 左单旋转(RR型)
- 失衡原因:结点的右孩子的右子树插入结点所致
- 调整策略:以结点的右孩子为轴,逆时针旋转,旋转以后,结点将作为其右孩子的左孩子,结点右孩子原来的左孩子作为结点的右孩子
- 举例(B、D、E三课子树高度为h):
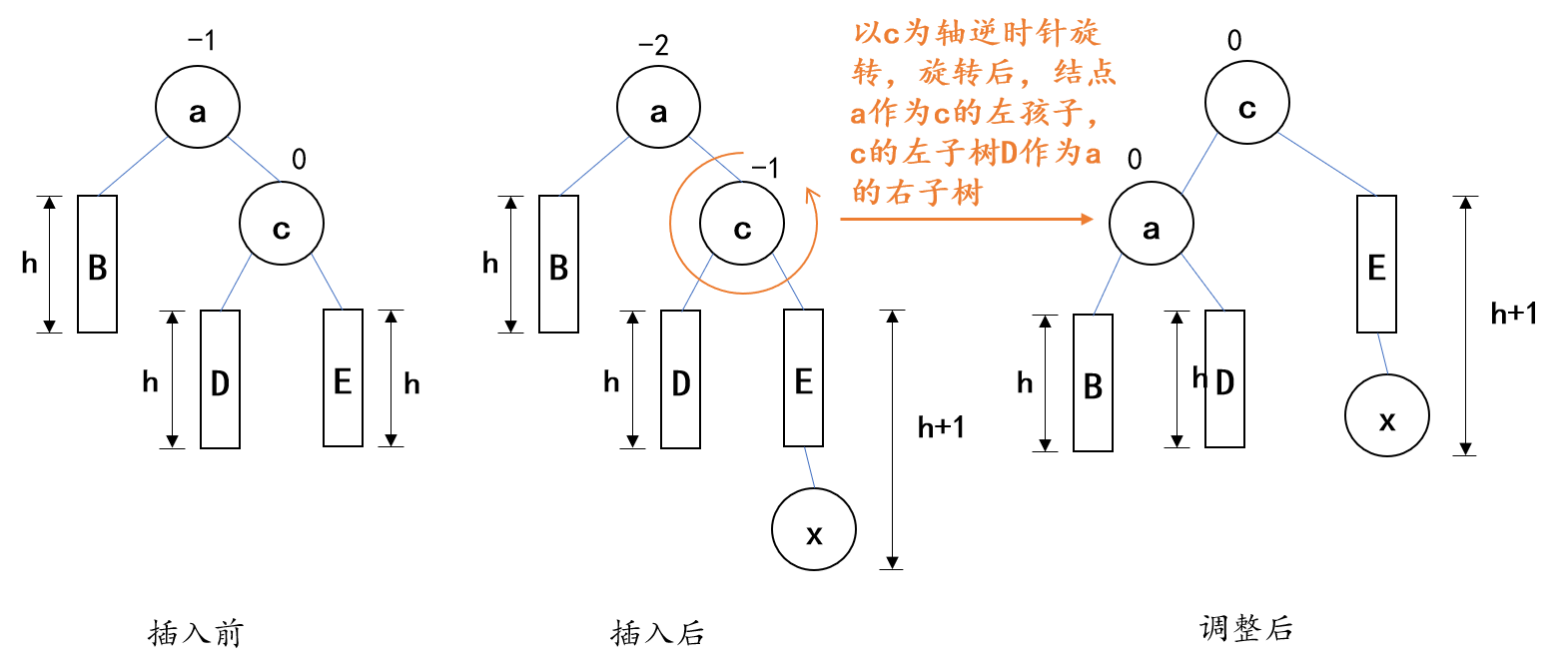
//左单旋转
//结点右孩子的右子树插入结点导致的失衡
//GetHeight函数:获取树的高度
template <typename T>
AvlNode<T>* AvlTree<T>::RR(AvlNode<T>* t)
{
AvlNode<T>* q = t->right;
t->right = q->left;
q->left = t;
t = q;
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
q->height = max(GetHeight(q->left), GetHeight(q->right)) + 1;
return q;
}
2.右单旋转(LL型)
- 失衡原因:结点的左孩子的左子树插入结点所致
- 调整策略:以结点的左孩子为轴,顺时针旋转,旋转以后,结点将作为其左孩子的右孩子,结点左孩子原来的右孩子作为结点的左孩子
- 举例(B、D、E三课子树高度为h)
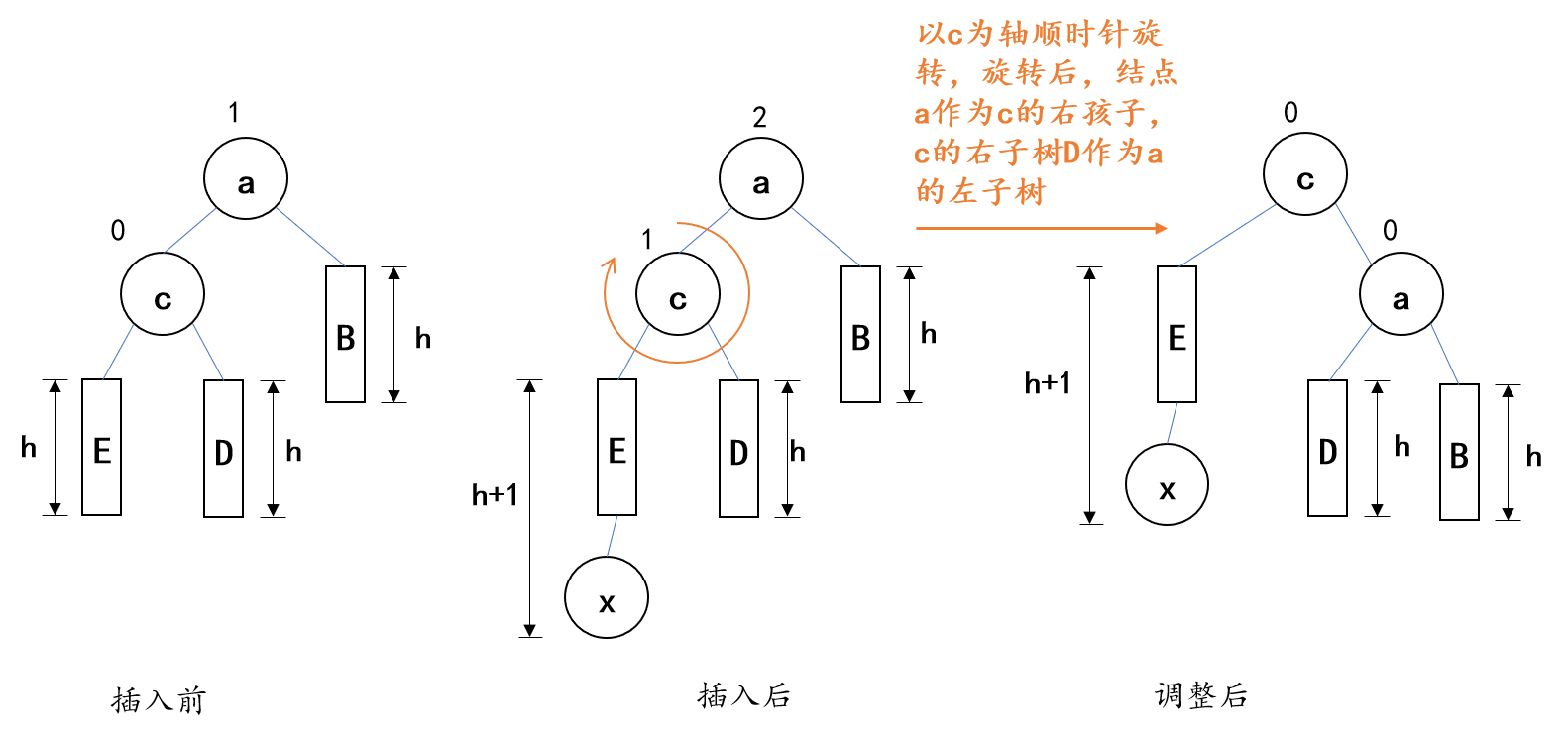
//右单旋转
//结点左孩子的左子树插入结点导致的失衡
//GetHeight函数:获取树的高度
template <typename T>
AvlNode<T>* AvlTree<T>::LL(AvlNode<T>* t)
{
AvlNode<T>* q = t->left;
t->left = q->right;
q->right = t;
t = q;
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
q->height = max(GetHeight(q->left), GetHeight(q->right)) + 1;
return q;
}
3.先左后右双向旋转(LR型)
- 失衡原因:结点的左孩子的右子树插入结点所致
- 调整策略:
- 第一次,对以结点b为根结点的子树,以结点c为轴,逆时针旋转,将结点c的左子树E作为结点b的右子树,将结点b作为结点c的左子树
- 第二次,以c为轴,顺时针旋转,c的右子树F作为a的左子树
- 举例(D、G两颗子树高度为h;E、F两颗子树高度为h-1)
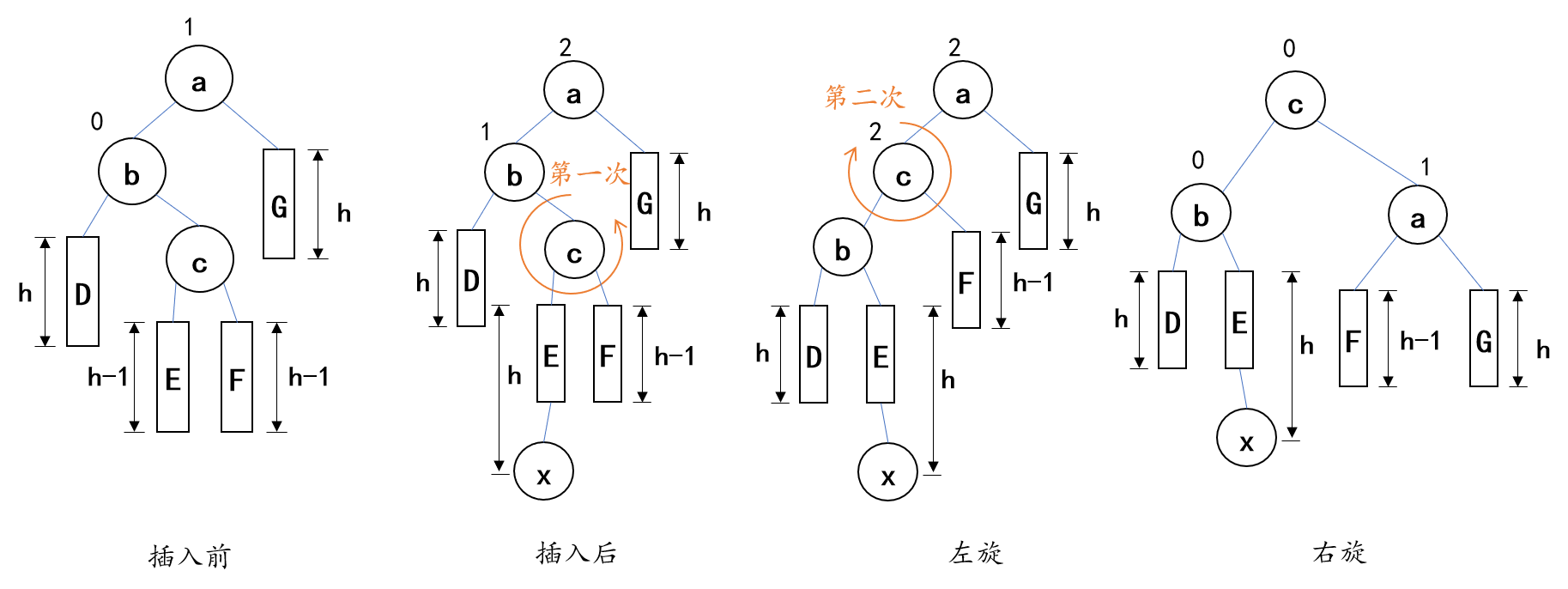
//先左后右双向旋转
//结点的左孩子的右子树插入结点导致的失衡
template <typename T>
AvlNode<T>* AvlTree<T>::LR(AvlNode<T>* t)
{
//双旋转可以通过两次单旋转实现
//对结点的左孩子进行RR旋转,再对结点进行LL旋转
RR(t->left);
return LL(t);
}
4.先右后左双向旋转(RL型)
- 失衡原因:结点的右孩子的左子树插入结点所致
- 调整策略:
- 第一次,以结点c为轴,顺时针旋转
- 第二次,以结点c为轴,逆时针旋转
- 举例
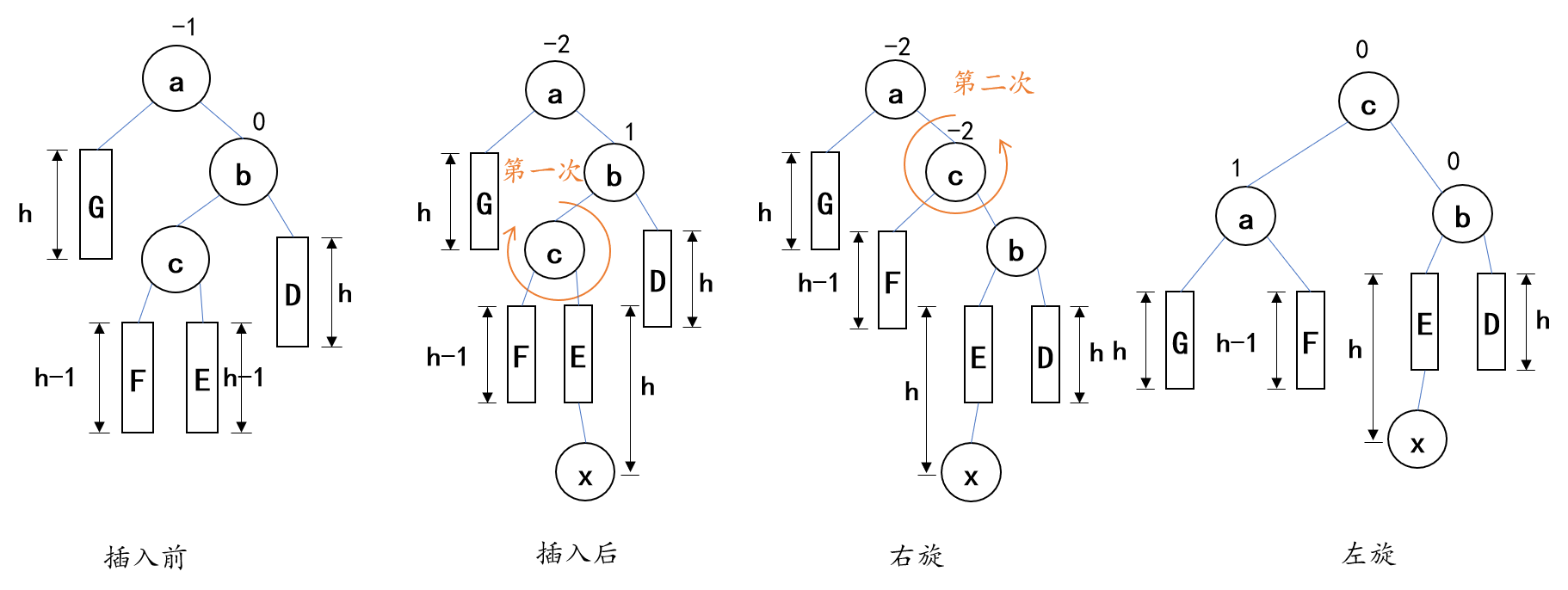
//先右后左双向旋转
//结点的右孩子的左子树插入结点导致的失衡
template <typename T>
AvlNode<T>* AvlTree<T>::RL(AvlNode<T>* t)
{
//双旋转可以通过两次单旋转实现
//对结点的右孩子进行LL旋转,再对结点进行RR旋转
LL(t->right);
return RR(t);
}
获取树的高度
//获取树的高度
template <typename T>
int AvlTree<T>::GetHeight(AvlNode<T>* t)
{
//空树
if (t == nullptr)
return -1;
//非空树时,返回树的高度
else
return t->height;
}
查找最大、最小值结点
//查找最大值结点
template <typename T>
AvlNode<T>* AvlTree<T>::FindMax(AvlNode<T>* t) const
{
//空树
if (t == nullptr)
return nullptr;
//由于是二叉排序树,结点的右子树为空,直接返回该结点
if (t->right == nullptr)
return t;
//若不符合上面两种情况,继续向结点右子树深入
return FindMax(t->right);
}
//查找最小值结点
template <typename T>
AvlNode<T>* AvlTree<T>::FindMin(AvlNode<T>* t) const
{
//空树
if (t == nullptr)
return nullptr;
//由于是二叉排序树,结点的左子树为空,直接返回该结点
if (t->left == nullptr)
return t;
//若不符合上面两种情况,继续向结点的左子树深入
return FindMin(t->left);
}
插入结点
//插入结点
template <typename T>
void AvlTree<T>::Insert(AvlNode<T>*& t, T x)
{
if (t == nullptr)//情况一:结点为空
t = new AvlNode<T>(x);
else if (x < t->data)//情况二:插入数据小于结点
{
Insert(t->left, x);
//判断平衡
if (GetHeight(t->left) - GetHeight(t->right) > 1)
{
// 分两种情况
// 插入结点在结点的左孩子的左子树上 左左 LL
// 插入结点在结点的左孩子的右子树上 左右 LR
if (x < t->left->data)//左左
t = LL(t);
else //左右
t = LR(t);
}
}
else if (x > t->data)//情况三:插入数据大于结点
{
Insert(t->right, x);
//判断平衡
if (GetHeight(t->right) - GetHeight(t->left) > 1)
{
// 分两种情况
// 插入结点在结点的右孩子的左子树上 左左 RL
// 插入结点在结点的右孩子的右子树上 左右 RR
if (x > t->right->data)
t = RR(t);
else
t = RL(t);
}
}
else //情况四:插入数据已经存在结点
;
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
}
删除结点
// 删除结点
template <typename T>
bool AvlTree<T>::Delete(AvlNode<T>*& t, T x)
{
//t为空 要删除的结点未找到 返回false
if (t == nullptr)
return false;
//要删除的结点找到了
else if (t->data == x)
{
//左右子树都非空
if (t->left != nullptr && t->right != nullptr)
{//在高度更大的那个子树上进行删除操作
//左子树高度大,删除左子树中值最大的结点,将其赋给根结点
if (GetHeight(t->left) > GetHeight(t->right))
{
t->data = FindMax(t->left)->data;
Delete(t->left, t->data);
}
else//右子树高度更大,删除右子树中值最小的结点,将其赋给根结点
{
t->data = FindMin(t->right)->data;
Delete(t->right, t->data);
}
}
else
{//左右子树有一个不为空,直接用需要删除的结点的子结点替换即可
AvlNode<T>* old = t;
t = t->left ? t->left : t->right;//t赋值为不空的子结点
delete old;
}
}
else if (x < t->data)//要删除的结点在左子树上
{
//递归删除左子树上的结点
Delete(t->left, x);
//判断是否仍然满足平衡条件
if (GetHeight(t->right) - GetHeight(t->left) > 1)
{
if (GetHeight(t->right->left) > GetHeight(t->right->right))
{
//RL双旋转
t = RL(t);
}
else
{//RR单旋转
t = RR(t);
}
}
else//满足平衡条件 调整高度信息
{
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
}
}
else//要删除的结点在右子树上
{
//递归删除右子树结点
Delete(t->right, x);
//判断平衡情况
if (GetHeight(t->left) - GetHeight(t->right) > 1)
{
if (GetHeight(t->left->right) > GetHeight(t->left->left))
{
//LR双旋转
t = LR(t);
}
else
{
//LL单旋转
t = LL(t);
}
}
else//满足平衡性 调整高度
{
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
}
}
return true;
}
查找结点
//查找结点
template <typename T>
bool AvlTree<T>::Contains(AvlNode<T>* t, const T x) const
{
if (t == nullptr)
return false;
if (x < t->data)
return Contains(t->left, x);
else if (x > t->data)
return Contains(t->right, x);
else
return true;
}
完整代码
#include <iostream>
#include <algorithm>
using namespace std;
#pragma once
//AvlNode
template <typename T>
struct AvlNode
{
T data; //数据域
int height; //结点所在高度
AvlNode<T>* left; //左孩子指针域
AvlNode<T>* right; //右孩子指针域
/*结构体初始化*/
AvlNode<T>(const T value) : data(value), left(nullptr), right(nullptr), height(0) {}
};
//AvlTree
template <class T>
class AvlTree
{
public:
//默认构造函数
AvlTree<T>() {}
//析构函数
~AvlTree<T>() {}
/*
* C++11标准
* 当使用默认构造函数时,类内成员必须都有类内初始值
* 当使用其他构造函数时,要将类内成员初始化,否则,即便该类内成员有类内初始值,其值也是未知的
*/
//二叉树根结点
AvlNode<T>* root{};//value is set via default member initialization
//插入结点
void Insert(AvlNode<T>*& t, T x);
//删除结点
bool Delete(AvlNode<T>*& t, T x);
/*
* 成员函数后加const表示该成员函数并不修改成员变量,增加程序的可读性、可靠性
*/
//查找是否存在给定值的结点
bool Contains(AvlNode<T>* t, const T x) const;
//中序遍历
void InorderTraversal(AvlNode<T>* t);
//前序遍历
void PreorderTraversal(AvlNode<T>* t);
//最小值结点
AvlNode<T>* FindMin(AvlNode<T>* t) const;
//最大值结点
AvlNode<T>* FindMax(AvlNode<T>* t) const;
private:
//求树的高度
int GetHeight(AvlNode<T>* t);
//右单旋转
AvlNode<T>* LL(AvlNode<T>* t);
//左单旋转
AvlNode<T>* RR(AvlNode<T>* t);
//先左后右双旋转
AvlNode<T>* LR(AvlNode<T>* t);
//先右后左双旋转
AvlNode<T>* RL(AvlNode<T>* t);
};
//查找最大值结点
template <typename T>
AvlNode<T>* AvlTree<T>::FindMax(AvlNode<T>* t) const
{
//空树
if (t == nullptr)
return nullptr;
//由于是二叉排序树,结点的右子树为空,直接返回该结点
if (t->right == nullptr)
return t;
//若不符合上面两种情况,继续向结点右子树深入
return FindMax(t->right);
}
//查找最小值结点
template <typename T>
AvlNode<T>* AvlTree<T>::FindMin(AvlNode<T>* t) const
{
//空树
if (t == nullptr)
return nullptr;
//由于是二叉排序树,结点的左子树为空,直接返回该结点
if (t->left == nullptr)
return t;
//若不符合上面两种情况,继续向结点的左子树深入
return FindMin(t->left);
}
//获取树的高度
template <typename T>
int AvlTree<T>::GetHeight(AvlNode<T>* t)
{
//空树
if (t == nullptr)
return -1;
//非空树时,返回树的高度
else
return t->height;
}
//右单旋转
//结点左孩子的左子树插入结点导致的失衡
template <typename T>
AvlNode<T>* AvlTree<T>::LL(AvlNode<T>* t)
{
AvlNode<T>* q = t->left;
t->left = q->right;
q->right = t;
t = q;
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
q->height = max(GetHeight(q->left), GetHeight(q->right)) + 1;
return q;
}
//左单旋转
//结点右孩子的右子树插入结点导致的失衡
template <typename T>
AvlNode<T>* AvlTree<T>::RR(AvlNode<T>* t)
{
AvlNode<T>* q = t->right;
t->right = q->left;
q->left = t;
t = q;
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
q->height = max(GetHeight(q->left), GetHeight(q->right)) + 1;
return q;
}
//先左后右双向旋转
//结点的左孩子的右子树插入结点导致的失衡
template <typename T>
AvlNode<T>* AvlTree<T>::LR(AvlNode<T>* t)
{
//双旋转可以通过两次单旋转实现
//对结点的左结点进行RR旋转,再对结点进行LL旋转
RR(t->left);
return LL(t);
}
//先右后左双向旋转
//结点的右孩子的左子树插入结点
template <typename T>
AvlNode<T>* AvlTree<T>::RL(AvlNode<T>* t)
{
//双旋转可以通过两次单旋转实现
//对结点的右结点进行RR旋转,再对结点进行LL旋转
LL(t->right);
return RR(t);
}
//插入结点
template <typename T>
void AvlTree<T>::Insert(AvlNode<T>*& t, T x)
{
if (t == nullptr)//情况一:结点为空
t = new AvlNode<T>(x);
else if (x < t->data)//情况二:插入数据小于结点
{
Insert(t->left, x);
//判断平衡
if (GetHeight(t->left) - GetHeight(t->right) > 1)
{
// 分两种情况
// 插入结点在结点的左孩子的左子树上 左左 LL
// 插入结点在结点的左孩子的右子树上 左右 LR
if (x < t->left->data)//左左
t = LL(t);
else //左右
t = LR(t);
}
}
else if (x > t->data)//情况三:插入数据大于结点
{
Insert(t->right, x);
//判断平衡
if (GetHeight(t->right) - GetHeight(t->left) > 1)
{
// 分两种情况
// 插入结点在结点的右孩子的左子树上 左左 RL
// 插入结点在结点的右孩子的右子树上 左右 RR
if (x > t->right->data)
t = RR(t);
else
t = RL(t);
}
}
else//情况四:插入数据在二叉树中有结点存在
;
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
}
// 删除结点
template <typename T>
bool AvlTree<T>::Delete(AvlNode<T>*& t, T x)
{
//t为空 要删除的结点未找到 返回false
if (t == nullptr)
return false;
//要删除的结点找到了
else if (t->data == x)
{
//左右子树都非空
if (t->left != nullptr && t->right != nullptr)
{//在高度更大的那个子树上进行删除操作
//左子树高度大,删除左子树中值最大的结点,将其赋给根结点
if (GetHeight(t->left) > GetHeight(t->right))
{
t->data = FindMax(t->left)->data;
Delete(t->left, t->data);
}
else//右子树高度更大,删除右子树中值最小的结点,将其赋给根结点
{
t->data = FindMin(t->right)->data;
Delete(t->right, t->data);
}
}
else
{//左右子树有一个不为空,直接用需要删除的结点的子结点替换即可
AvlNode<T>* old = t;
t = t->left ? t->left : t->right;//t赋值为不空的子结点
delete old;
}
}
else if (x < t->data)//要删除的结点在左子树上
{
//递归删除左子树上的结点
Delete(t->left, x);
//判断是否仍然满足平衡条件
if (GetHeight(t->right) - GetHeight(t->left) > 1)
{
if (GetHeight(t->right->left) > GetHeight(t->right->right))
{
//RL双旋转
t = RL(t);
}
else
{//RR单旋转
t = RR(t);
}
}
else//满足平衡条件 调整高度信息
{
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
}
}
else//要删除的结点在右子树上
{
//递归删除右子树结点
Delete(t->right, x);
//判断平衡情况
if (GetHeight(t->left) - GetHeight(t->right) > 1)
{
if (GetHeight(t->left->right) > GetHeight(t->left->left))
{
//LR双旋转
t = LR(t);
}
else
{
//LL单旋转
t = LL(t);
}
}
else//满足平衡性 调整高度
{
t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
}
}
return true;
}
//查找结点
template <typename T>
bool AvlTree<T>::Contains(AvlNode<T>* t, const T x) const
{
if (t == nullptr)
return false;
if (x < t->data)
return Contains(t->left, x);
else if (x > t->data)
return Contains(t->right, x);
else
return true;
}
//中序遍历
template <typename T>
void AvlTree<T>::InorderTraversal(AvlNode<T>* t)
{
if (t)
{
InorderTraversal(t->left);
cout << t->data << ' ';
InorderTraversal(t->right);
}
}
//前序遍历
template <typename T>
void AvlTree<T>::PreorderTraversal(AvlNode<T>* t)
{
if (t)
{
cout << t->data << ' ';
PreorderTraversal(t->left);
PreorderTraversal(t->right);
}
}
int main()
{
AvlTree<int> tree;
int value;
int tmp;
cout << "请输入整数建立二叉树(-1结束):" << endl;
while (cin >> value)
{
if (value == -1)
break;
tree.Insert(tree.root, value);
}
cout << "中序遍历:";
tree.InorderTraversal(tree.root);
cout << "\n前序遍历:";
tree.PreorderTraversal(tree.root);
cout << "\n请输入要查找的结点:";
cin >> tmp;
if (tree.Contains(tree.root, tmp))
cout << "查找结点成功!" << endl;
else
cout << "值为" << tmp << "的结点不存在!" << endl;
cout << "请输入要删除的结点:";
cin >> tmp;
tree.Delete(tree.root, tmp);
cout << "删除后的中序遍历:";
tree.InorderTraversal(tree.root);
cout << "\n删除后的前序遍历:";
tree.PreorderTraversal(tree.root);
}
测试结果:






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!