首先要感谢叉姐的指导Orz
这一类问题的DP方程都有如下形式
dp[i] = w(i) + max/min(a(i)*b(j) + c(j)) ( 0 <= j < i )
其中,b, c均为j的单调函数。通常情况下a(i)也是单调的,a(i)不单调时就只能二分查找了。
这里讲一下当c(j)单调递增,b(j)单调递减,原方程求min的情况
对于同一j,b(j),c(j)为常数,而a(i)为变量,令y = b(j) * x + c(j),则y为线性函数
我们把( 0 <= j < i )的直线均表示在平面上,则如下图所示。
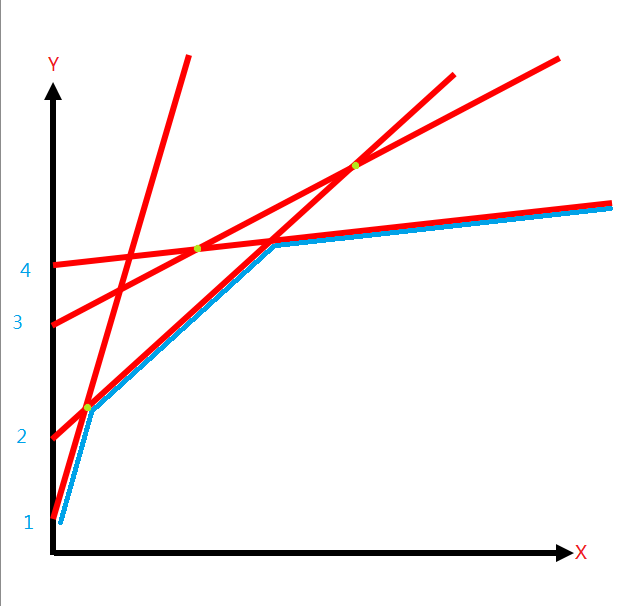
显然,对于不同的dp[i],我们要求的是在对应x = a(i)下所有直线的最小值
看图我们可以发现,就是这些直线的下半平面交的边缘组成的分段函数,就是我们要求的函数
那么怎么维护这个半平面呢
首先b(j)最小的直线,必然会在足够大处,取得所有直线的最小值
我们在维护的过程中,总是在原半平面交的基础上,加上一个c(j)最大,b(j)最小的直线
这个时候,这条直线必然会加入半平面交当中。
同时,有可能会导致有些直线被遮蔽而退出集合。
我们可以发现,如果j=k的直线没有被遮蔽,那么j=[0,k)的直线也显然不会被遮蔽。
所以我们只需要从原来的半平面交最大的j开始不停的向内找,直到找到第一个没被遮蔽的直线就可以了。
那么直线什么时候会被遮蔽呢?
直线只剩两条的时候,显然不会有直线被遮蔽→ →
观察图中的直线1,2,3以及直线2,3,4。
2没有被遮蔽,是因为2和1的交点在2和3的交点左边。
而3被遮蔽,是因为3和2的交点在3和4的交点的右边。
所以只需要求交点然后比较大小就可以了。(两直线求交,初中知识,相信大家都会,请自行计算)
这里需要注意的是,求交点需要用到除法。但是除法容易出现精度问题,我们要把除法在比较的时候移到另一侧变成乘法,这个时候记得注意正负变号。
这个维护过程,考虑每个直线最多进出队列一次,复杂度总计O(n)
维护好半平面集合,后,求x = a(i)时的值,只需要二分判断落在哪个直线的交点区域内就好了。
特殊的,如果a(i)也单调,则可以像单调队里那样从头部一一剔除的方法,这里不多做介绍。
理解上述部分后,假如b(j),c(j)都不单调,问题则转变为动态半平面交。
另外,其实有没有发现写起来和凸包的理解非常像?叉姐告诉我们,其实根据平面的点与直线的对偶,凸包和半平面交问题是完全等价的。
附HDU 3669代码

1 #include<cstdio> 2 #include<cstring> 3 #include<cmath> 4 #include<cstdlib> 5 #include<algorithm> 6 using namespace std; 7 typedef long long ll; 8 const int N=50005; 9 10 pair<int,int> a[N],s[N]; 11 int n,m; 12 13 int l,r; 14 pair<int,ll> q[N]; 15 16 int x,y; 17 ll dp[2][N]; 18 19 inline void push(int k,ll b){ 20 while(l<r && (q[r].second-q[r-1].second)*(q[r].first-k)>=(b-q[r].second)*(q[r-1].first-q[r].first)) r--; 21 q[++r]=make_pair(k,b); 22 } 23 24 inline void pop(ll x){ 25 while(l<r && (q[l].first - q[l+1].first)*x >= q[l+1].second - q[l].second) l++; 26 } 27 28 int main(){ 29 while(~scanf("%d%d",&n,&m)){ 30 for(int i=0;i<n;i++)scanf("%d%d",&a[i].first,&a[i].second); 31 sort(a,a+n); 32 int cnt=1,mxb=a[n-1].second; 33 s[0]=a[n-1]; 34 for(int i=n-2;i>=0;i--)if(a[i].second>mxb){ 35 mxb = a[i].second; 36 s[cnt++]=a[i]; 37 } 38 n=cnt; 39 ll mxa=s[0].first; 40 for(int i=0;i<n;i++) dp[0][i]=mxa*s[i].second; 41 ll ans=dp[0][n-1]; 42 x=0; 43 y=1; 44 if(m>n) m=n; 45 for(int k=1;k<m;k++){ 46 l=0;r=-1; 47 push(s[k].first,dp[x][k-1]); 48 for(int i=k;i<n;i++){ 49 pop(s[i].second); 50 dp[y][i]=q[l].second+(ll)q[l].first*s[i].second; 51 push(s[i+1].first,dp[x][i]); 52 } 53 x^=1; 54 y^=1; 55 if(dp[x][n-1]<ans) ans=dp[x][n-1]; 56 else break; 57 } 58 printf("%I64d\n",ans); 59 } 60 return 0; 61 }




