多目标优化总结by知乎 @ 张大快

多目标优化的解集

单目标优化的最优解定义在多目标优化问题（MOO）问题中通常不适用。MOO的解集通常可以通过绝对最优解、有效解和弱有效解来描述。
先对多目标中的相等、严格小于、小于和小于且不相等进行说明。

\[\left\{ \begin{array}{} 相等&y=z\Leftrightarrow y_i=z_i,i=1,2,\cdots,N\\ 严格小于&y<z\Leftrightarrow y_i<z_i,i=1,2,\cdots,N\\ 小于&y \leqq z\Leftrightarrow y_i\leq z_i,i=1,2,\cdots,N\\ 小于且不相等（支配）&y\leq z\Leftrightarrow y_i\leq z_i,i=1,2,\cdots,N,y \neq z \end{array} \right. \]

Pareto 支配（Pareto Dominance）

定义： \(\forall x_{1},x_{2}\in R^{N}\),如果对于所有的\(k=1,\cdots,K\)都有\(f_k(x_1)\leq f_k(x_2)\),则称\(x_1\)\(\color{navy}{支配}\)\(x_2\)。

Pareto 解集：绝对最优解

定义： 设\(x^* \in D\),如果不存在\(x\in D\),使得\(f(x) \leq f(x^*)\);即下面条件不成立：

\[f_k(x) \leq f_k(x^*) ,and \exists i,f_i(x)<f_i(x^*),i \in [1,k] \]

则 \(x^*\)是MOO问题的\(\color{navy}{有效解}\)。

有效解也叫\(\color{navy}{帕累托最优解}\)，其含义是，如果\(x^*\)是帕累托最优解，则找不到这样的可行解\(x \in D\)，使得\(f(x)\)的每个目标值比\(f(x^*)\)的目标值坏，并且\(f(x)\)至少有一个目标比\(f(x^*)\)的相应值好。即\(x^*\)是最好的，不能再进行改进（帕累托改进）。\(\color{red}{(可以持平、可以一好一坏，但是不可以一平一好或者两个全比我好)}\)

Pareto解集：弱有效解

定义：设\(x^*\in D\)，如果不存在\(x \in D\)，使得\(f(x) < f(x^*)\)；即

\[f_k(x) < f_k(x^*),and, \forall k\in [1,k] \]

则\(x^*\)是MOO问题的弱有效解.

其含义是如果\(x^*\)是弱有效解，则找不到这样的可行解\(x \in D\),使得\(f(x)\)的每个目标值都比\(f(x^*)\)的目标值严格的好。（不存在相等）

Pareto最优解集（Pareto-optimal Set）

定义：给定的MOO问题的有效解（帕累托最优解）构成的解集，称这个解集为Pareto-optimal Set，简称PS。

这个集合中的解都是互相非支配的，也即两两不是支配关系。

Pareto 最优前沿（Pareto-optimal front）

定义：Pareto-optimal Set 中每个解对应的目标值向量组成的集合称之为Pareto最优前沿（Pareto-optimal front），简称PF：

\[PF = \{F(x)|x \in PS\} \]

如图所示：

## 多目标优化的最优性条件 $\color{navy}{约束规格}$的定义：对优化问题的约束函数，附加某些限制条件，使得其最优解满足的最优性条件。 下面给出一个严格条件下多目标优化的充分必要条件。

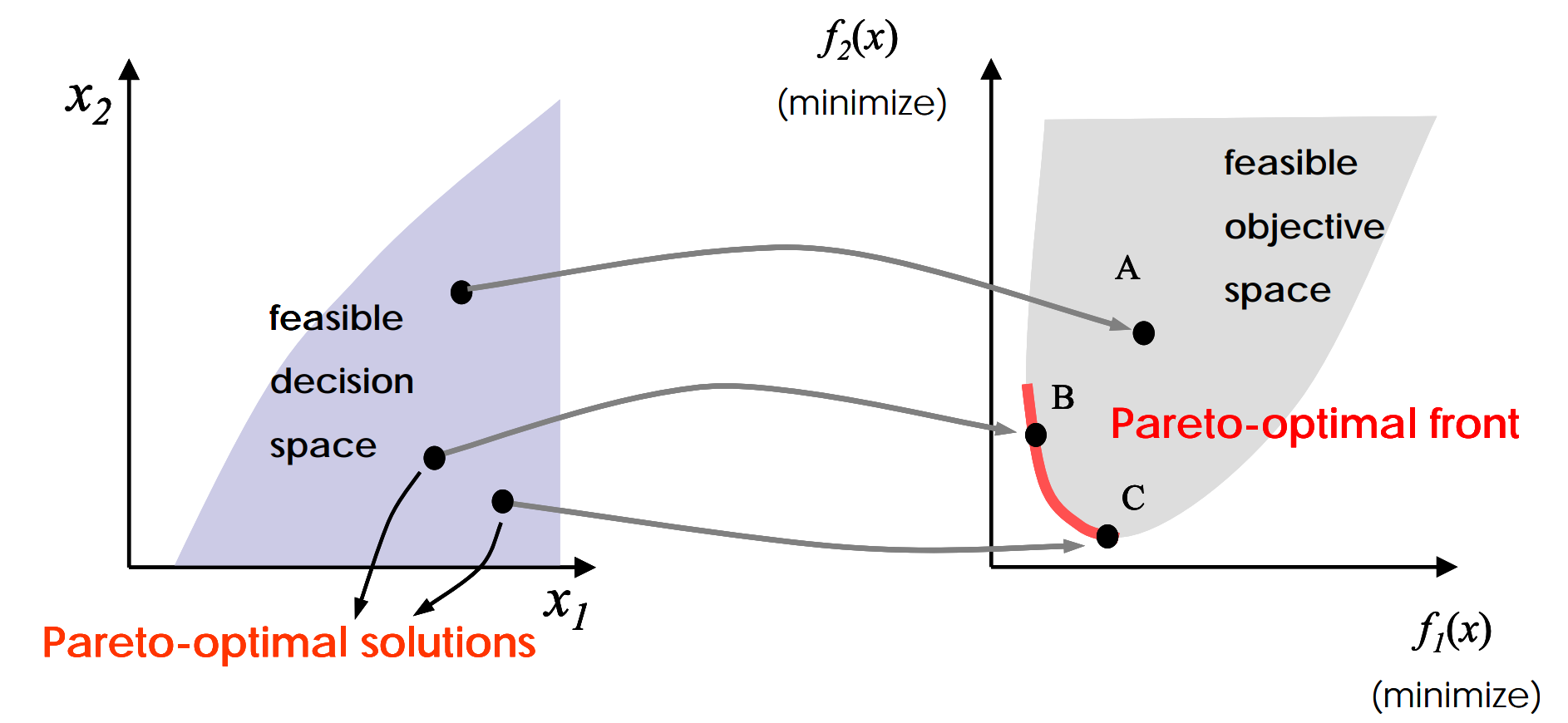
定理：设\(f(x),g(x)\)为凸函数，且在\(x\in D\)处可微，\(h(x)\)为线性函数，且\(\hat{D}=x \in D|f(x) \leq f(\hat{x})\)满足KKT约束规格，则\(x^*\)是MOO的有效解的充分必要条件是存在\(\lambda \in R^K,u \in R^M,v \in R^L\)使得

\[\left\{ \begin{array}{} \triangledown_x L(x^*,\lambda^*,v^*) = \triangledown f(x_*)\lambda^*+\triangledown g(x_*)u^*+\triangledown h(x_*)v^* = 0 \\ u^{*T}g(x_*)=0\\ \lambda^*>0,u^*\geq 0 \end{array} \right. \]

\(\color{red}{chao，都不满足凸函数，也不可微, 要命}\)