leetcode_动态规划_53_最大子数组和

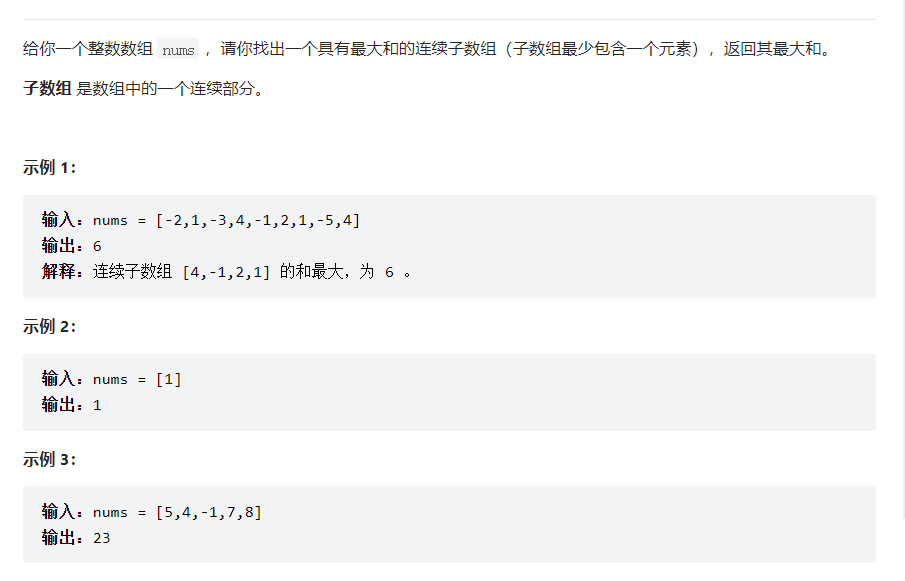
题目描述

解题过程

暴力滑窗

本菜鸡看题目第一眼就暗喜，这还不简单嘛，直接滑窗滑过去，记录下最大的窗就可以了吗。窗口左节点在满足下面两种条件的情况下，会向后移动。

1. 本次滑窗内的连续数组和小于等于零
2. 本次滑窗的右节点移动到末尾
   直接手撸代码如下，轻松通过三个测试案例

nums = [-2,1,-3,4,-1,2,1,-5,4]
left,right = 0,0
temp = nums[0:1]
res = nums[0]
# res = 1
N = len(nums)
while left <= N :
    if right >= N:
        left += 1
        right = left
        # print('第一个')
    if res < 0:
        left += 1
        right = left
        # print('第二个')
    temp = nums[left : right + 1]
    if temp == []:
        break
    res = max(res,sum(temp))
    right += 1
print(res)

点击提交，没想到后台直接给了个长度1w的数组让跑，直接显示测试超时。还是乖乖看题解去吧

题解—动态规划

不得不说，真是妙的很。思路很清晰，找到了状态转移方程。首先定义f(i)为以i结尾的最大连续数组和。i遍历一遍得到f(i)组成的数组，再从中找到最大值即可。其中，f(i)转移的方程为f(i)=max{f(i-1)+nums(i),nums(i)}. （白手起家也不要接之前的烂摊子）

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        N = len(nums)
        temp = [nums[0],]
        for i in range(1,N):
            temp.append(max(temp[i - 1] + nums[i],nums[i]))

        return max(temp)