遗传算法求解最大值(含matlab代码)
新手,有什么不足的或者不准确的,大家希望能热心指出,一起讨论交流
问题描述
求解函数f(x) = x * sin(10pi * x) + 2 在区间[-1,2]上的最大值,要求精度10^-6.
代码部分
具体的理论部分不进行过多的解释,网上有很多详细的帖子。直接上代码,一共有Ga_max.m、bin2dec.m、selection.m、crossover.m、mutation.m五部分组成,第一个是求解最大值的主函数,后面四个分别是二进制转十进制、选择、交换、和变异函数
主函数部分
首先确定种群的大小N和每个个体的编码长度L,随机生成一个只含0-1的N x L的矩阵P,也就是初始化种群。然后确定进化的相关参数,有:交叉的概率、变异的概率和要进化迭代的次数。
初始化完成后开始进化,也就是开始for循环,首先对x进行解码码,对个体(二进制串)转化成十进制,然后计算个体的适应度。接着要进行遗传操作(选择、交叉、变异),完成种群更新。计算新种群的适应度,以及最优个体和最优适应度。
迭代完成后,最后一代的最优个体和最优个体即为所求。
其中,遗传算法求解最优解时,首先要将实际问题的参数集进行编码化,常见的类型有二进制编码和浮点数编码。
这里采用二进制编码,因为需要精度达到10-6,也就是说编码长度L需要满足:2L > (2-(-1)) * 10^6,这里编码长度L选取22。
%%
clc
clear
close all
%%
% 问题 求解f再[x_min,x_max]上的最大值
%需要求解再区间内函数的最大值
f = 'x .* sin(x .* 10 * pi) + 2';
x_min = -1;x_max = 2; %自变量取值区间
%初始化参数
N = 100; %种群大小
L = 22; %编码长度
P = zeros(N,L); %N个个体,每个个体的编码长度为L,由01构成
%初始化种群
P = round(rand([N,L]));
%% 迭代
%迭代初始化
pc = 0.6; %交叉概率
pm = 0.05; %变异概率
gen = 500; %迭代次数
fit_mean = [];%平均适应度
fit_opt = [];%最优适应度
iter = 1;%迭代计数器
%开始进化
for iter = 1:gen
x = bin2dec(P(:,1:L),x_min,x_max);
fit = eval(f);
%select
P_new = selection(P,fit);
%crossover
P_new = crossover(P_new,pc);
%mutation
P_new = mutation(P_new,pm);
%更新种群
P = P_new;
%计算新种群的适应度
x = bin2dec(P(:,1:L),x_min,x_max);
fit = eval(f);
[opt,loc] = max(fit);%记录最优适应度和最优个体
fit_mean(iter) = mean(fit); %记录适应度均值
fit_opt(iter) = opt; %记录最佳适应度
%画图部分
%初始选取的基因位置
if iter == 1
pause(1)
figure(1)
cla
fplot(f,[x_min,x_max]);
hold on
plot(x,fit,'r*')
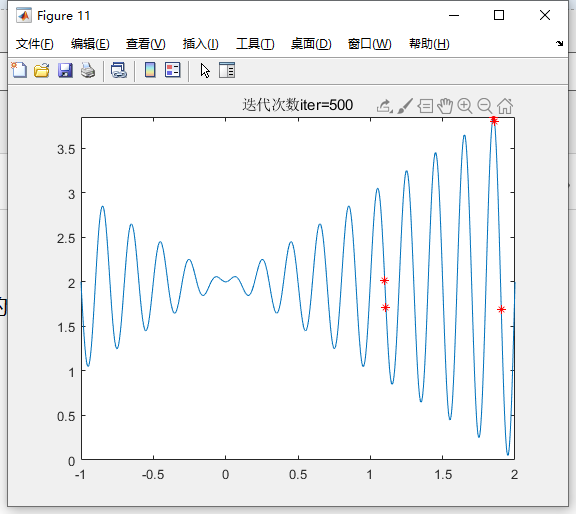
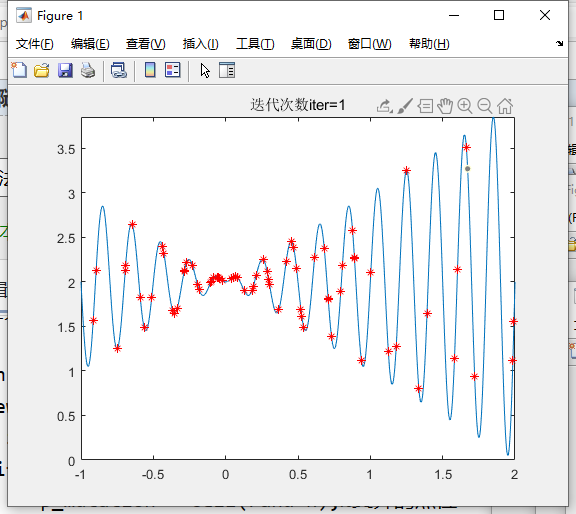
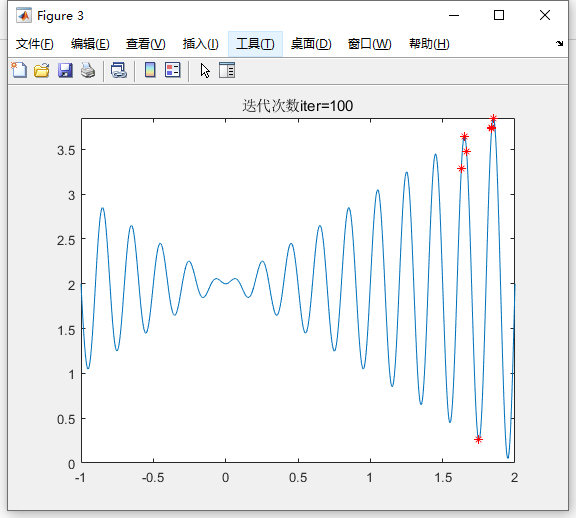
title(['迭代次数iter=',num2str(iter)])
end
%基因位置变化记录
if mod(iter,50) == 0
pause(1)
figure(1)
cla
fplot(f,[x_min,x_max]);
hold on
plot(x,fit,'r*')
title(['迭代次数iter=',num2str(iter)])
end
iter = iter + 1;
end
fprintf('The Best X -->%5.6f\n',x(loc));
fprintf('The Best Y -->%5.6f\n',opt);
二进制转十进制函数
注意这里的十进制是指对应解区间的十进制数。如果二进制正常转到十进制时K,那么这里还要再对k进行“归一化”。有如下关系:
x = x_min + (x_max - x_min) * k / (2^L - 1)
% 二进制转十进制
function num = bin2dec(num_bin,n_min,n_max)
% ```
% num_bin:一串二进制数
% n_min,n_max:归一化的上下区间
% 二进制转化为十进制,再把十进制的数压缩到[n_min,n_max]区间上
num_bin = fliplr(num_bin);%二进制串左右反转
[m,n] = size(num_bin);%m个长度n的二进制串
weight = 0:1:n-1;
weight = ones(m,1) * weight;%[m,n]的权重矩阵,每一行都是0,1,2...n-1,2的多少次方
num_dec = sum((num_bin .* 2.^weight)'); %每一分位成对应的权重求和 %转置是因为sum是列求和
num = n_min + (n_max-n_min) * num_dec ./ (2^n - 1);
end
选择函数
选择采用轮盘赌选择的方式,选择个体i的概率 pi = fi / sum(fi)。出现的频数越大,被选中的概率就越大,优势基因更能够在种群中扩散。注意代码中里产生的随机数是与分布函数做比较的。
%% selection
function P_new = selection(P,fit)
% % % %
% 采用轮盘选择法来选择需要复制的基金
% P_new : 是新的基因组
% P: 是旧基因组
% fit: 是就基因组所对应的适应度
[m,n] = size(P); %种群中m个个体
p_fit = fit./sum(fit); %概率
F_fit = cumsum(p_fit); %分布函数
temp = sort(rand(1,m)); %随机生产m个概率
fit_p = 1;
new_p = 1; %两个指针,一个指新种群,一个指旧的
while new_p <= m %需要循环m次,把新基因组填满
if temp(new_p) < F_fit(fit_p) %根据随机参数的概率与分布函数作比较,得出要选择的基因
P_new(new_p,:) = P(fit_p,:); %选择后完成复制
new_p = new_p + 1; %指针加一,寻找下一个要选择的
else
fit_p = fit_p + 1; %在旧种群中,没有选中这一个体。加一对下一个进行判断
end
end
交叉函数
% crossover
function P_new = crossover(P,pc)
% % %
% P_new: 新种群
% P : 旧种群
% pc : 交叉概率
[m,n] = size(P);
for i = 1:2:m-1
if rand < pc %发生交叉
p_cross = ceil(rand * n); %发生交叉的点位,两个个体这一点之后的所有基因交换
P_new(i,:) = [P(i,1:p_cross - 1),P(i + 1,p_cross:n)];
P_new(i+1,:) = [P(i + 1,1:p_cross - 1),P(i,p_cross:n)];%两个个体交换交叉点后的基因序列
else
P_new(i,:) = P(i,:);
P_new(i + 1,:) = P(i + 1,:);
end
end
变异函数
function P_new = mutation(P,pm)
% % %
% 变异操作
[m,n] = size(P);
P_new = P;
for i = 1:m
if rand < pm %发生变异
p_mutation = ceil(rand*n);%变异的点位
if P_new(i,p_mutation) == 0
P_new(i,p_mutation) = 1;
else
P_new(i,p_mutation) = 0; %对变异点的记忆值进行反转
end
end
end
结果展示
初始基因位置
迭代100次
迭代200次
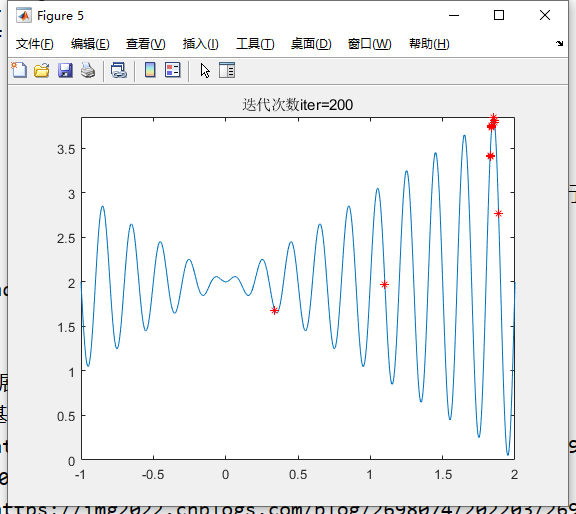
迭代300次
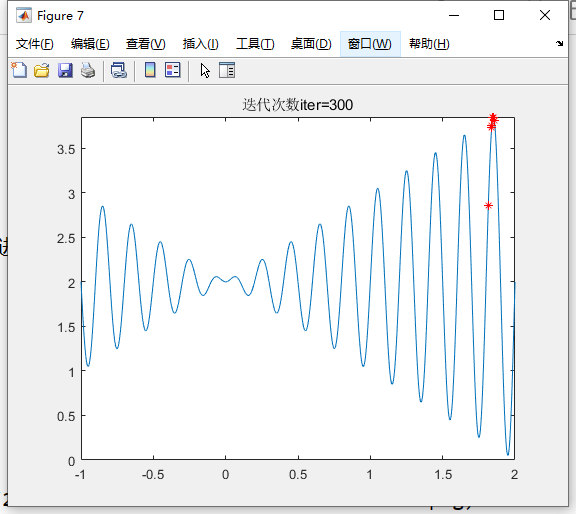
迭代400次
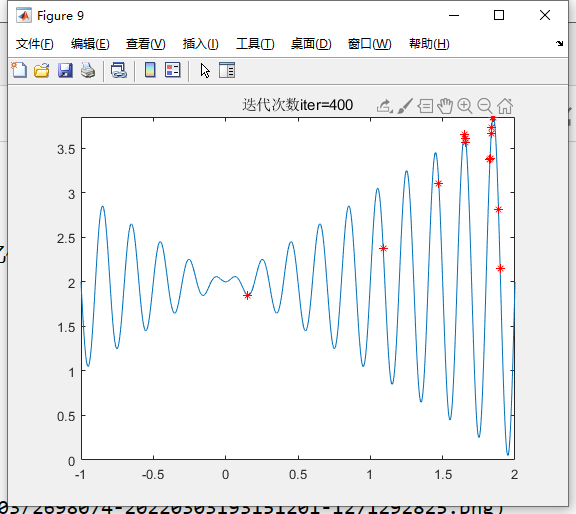
迭代500次