$Abstract^2 Interpretation$

POPL'19

本文提出 \(A^2I\)，即 \(Abstract^2 Interpretation\)，也叫做 meta-abstract interpretation，是指使用抽象解释（abstract interpretation）分析静态程序分析器（static program analyser）的特性。

静态程序分析（static program analysis）是自动提取程序动态行为特性的技术。抽象解释是一种生成静态程序分析方法的理论框架，思想是提取程序特性以逼近程序语义（semantics）。

要理解 \(A^2I\)，就得先理解 AI（抽象解释，下同）。

我们以单调数据流分析框架（monotone dataflow analysis framework）为基础开始讲。单调框架包括三部分：

1. 特性格（property lattice），这里说一下，所谓特性，一般就是指抽象值（abstract value）；
2. 格中元素的含义，即如何解释分析的结果；
3. 转移函数（transfer function）。

单调框架只是一种表示静态分析的数学格式，它的问题在于其正确性证明一般依赖于寻找不变量（invariant），每个分析的正确性证明是独立的（ad-hoc）。

为此，抽象解释提出一种构建程序分析的系统化的方法。需要：

1. 特性格；
2. 表示函数（representation function），即如何解释格中的元素。

然后可以定义出满足一定条件的可计算函数作为转移函数。

抽象解释对分析的定义是增量的，分析由正确性易证的“分析”开始，即收集语义（collecting semantics），收集程序的准确信息，但是直接对其静态分析是困难甚至不可能的，因为特性空间（property space）太大或不满足升链条件（ACC: Ascending Chain Condition，满足ACC也称为诺特的，Noetherian。\(a_1 \leq a_2 \leq \cdots, \exist n, \forall m > n, a_m = a_n\)）。接着我们计算得到收集语义的一个近似，即由基础分析（basic analysis）得到精化分析（refined analysis）。最后不断迭代精化（近似）过程直到得到一个可计算函数。

具体程序执行（concrete program execution）可以表示如下：

\[v_0 \rightsquigarrow v_1 \rightsquigarrow \cdots \rightsquigarrow v_i \cdots \]

\(V = \lbrace v_i \rbrace\) 是值或状态的集合，\(\rightsquigarrow\) 是传递关系，当具体执行是确定性的（deterministic）时候，传递关系就是一个函数。

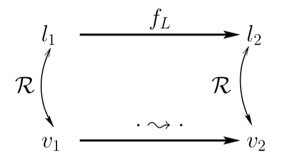
而程序分析，即程序的抽象执行（abstract execution）可以表示为：

\[l_0 \mapsto l_1 \mapsto \cdots \mapsto l_i \cdots \]

其中 \(l_{i+1} = f_L(l_i)\)，\(f_L : L \rightarrow L\) 是一个函数，L 是完全格（complete lattice）。在 \(A_2I\) 的论文中，作者严格区分了完全格与：1）dcpo（有向偏序），每个子集都有上确界；2）cpo（完全偏序），包含最小元素的dcpo。

即 \(l_i\) 是 \(v_i\) 的抽象，由此为了提供正确性证明的机制，需要定义两者之间一种正确性关系（correctness relation），\(R \subseteq V \times L\)。

1. \(\forall v, l_1, l_2, (vRl_1) \bigwedge (l_1 \sqsubseteq l_2) \rightarrow (vRl_2)\)，即在特性格 L 中，\(l_1\) 是比 \(l_2\) 更精确的对 v 的抽象；
2. \(\forall v, \forall L^{'} \subseteq L, (\forall l \subseteq L^{'}, (vRl)) \rightarrow vR(\sqcap L^{'})\)，即 \(\sqcap L^{'}\) 是 v 的最精确近似（valid approximation）。

特性空间是格是为了比较抽象值之间的精度，更小更精确，更大更安全（仍然正确）。

由此已经证明了抽象的正确性，由归纳也易证传递的正确性。即我们已经得到了基础分析。

给定一个程序点 p，由 \(v_0\) 出发的所有路径都会达到 p，但计算所有路径的抽象值得到特性格中的一个元素是不可行的。由数据流方程（dataflow equation）可以计算不动点（fixed point），但需要满足两个条件：

1. 单调；
2. L满足ACC。

这是传统的计算程序分析结果的方法。

但是很多时候分析收敛（converge）很慢，或者不满足 ACC。为此抽象解释使用一个更小（更精确）的格 M 来对 L 进一步抽象，L 和 M 之间满足伽罗瓦连接（Galois connection）\(\langle L, \alpha, \gamma, M\rangle\)。其中 \(\alpha\) 和 \(\gamma\) 是单调函数，\(\alpha\) 把 L 中的元素映射到 M 中，称为抽象化函数（abstraction function）；\(\gamma\) 把 M 中的元素映射到 L 中，称为具体化函数（concretization function）。且满足两个约束：

1. \(\alpha \circ \gamma \sqsubseteq_M \lambda m.m\)，即具体化不损失精度；
2. \(\gamma \circ \alpha \sqsupseteq_L \lambda l.l\)，即抽象化可能损失精度。

由此我们得到精化分析。（可以证明S也满足正确性关系。）

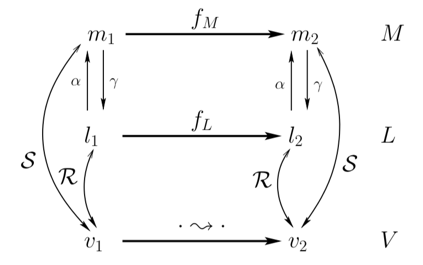
到这里我们就说明了 slides 第 8 页的：

1. 语义是抽象解释的实例；
2. 收集语义是抽象解释的实例；
3. 对抽象解释实例的抽象是抽象解释的实例。

所以，由对程序特性的抽象（AI）上升到对程序分析特性的抽象（\(A^2I\)）是可行的。

回到之前的讨论，有了精化分析之后，不动点的计算可以转化为求 AKS（Ascending Kleene Sequence）的极限，AKS 可以表示为 \((f^n(\tau))_n\)，其中 \(f : L \rightarrow L\) 是单调的传递函数，\(\tau\) 以 L 的底元作为起始值。若 AKS 会趋于稳定（连续格，有限格上连续和单调等价），则其稳定于 f 的最小不动点 lfp(f)。但有时并不会趋于稳定，或者是迭代太慢，为此又引入 widening 技术来计算 AKS 的上近似（upper approximation），AAS（Ascending Approximation Sequence），它有着更快的收敛速度。由此求得 lfp(f) 的上近似。（不考虑抽象解释，数据流分析也可以使用widening，有略微不同。）

widening 算子 \(\nabla : L \times L \rightarrow L\) 定义如下：

1. \(\nabla\) 是一个上界（upper bound）算子，即 \(\forall l_1, l_2, l_1 \sqsubseteq l_1 \nabla l2, l_2 \sqsubseteq l_1 \nabla l2\)；
2. 对 L 中所有的上升链 \((l_n)_n\)，上升链 \((l_n^{\nabla})_n\)（也在 L 中）必趋于稳定。

由链的构造易知：

\[l_0^{\nabla} = l_0, l_1^{\nabla} = l_0^{\nabla} \nabla l_1 = l_0 \nabla l_1, l_2^{\nabla} = l_1^{\nabla} \nabla l_2 = l_0 \nabla l_1 \nabla l_2, \cdots \]

稳定性易证。将上升链扩展到单调函数也同理。

narrowing 算子与 widening 类似，而这两个算子的实质就是：分析程序分析的不动点迭代的变化，来计算下一个迭代。其实已经有了 \(A^2I\) 的雏形。作者把这一类归入 online meta-analysis（during program analysis），此外还有 offline meta-analysis（before/after program analysis）。

为了支持A2I，需要对抽象解释做一些修改，把收集语义扩展到跟踪语义（trace semantics），即由可达抽象值集合扩展到抽象解释器不动点迭代的序列。以间隔分析（interval analysis）为例，考虑下面的程序：

\[x = 0; while^{l_1} (true) \lbrace x = x + 2;^{l_2} \rbrace \]

收集语义下的 Jacobi 迭代为：

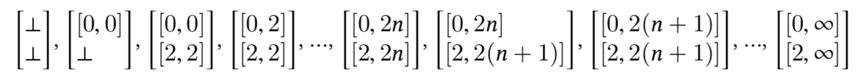
对于由底元开始的序列

\[\begin{bmatrix} x_{11} \\ x_{21} \end{bmatrix}, \begin{bmatrix} x_{12} \\ x_{22} \end{bmatrix}, \cdots, \begin{bmatrix} x_{1i} \\ x_{2i} \end{bmatrix}, \cdots \]

推导规则为：

\[\begin{bmatrix} x_{1(i+1)} \\ x_{2(i+1)} \end{bmatrix} = \begin{bmatrix} [0, 0] \sqcup x_{2i} \\ x_{21} \bigoplus [2, 2] \end{bmatrix} \]

跟踪语义下的Jacobi迭代则是：

其包含过程信息。

将对其抽象定义为：

根据该定义手推前5项：

通过对常量传播（constant propagation）分析的抽象，可以将以上迭代加快如下：

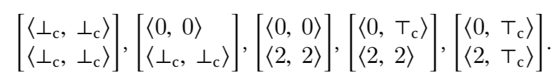
其推导规则为：

\[\begin{bmatrix} \langle l_{1(i+1)}, h_{1(i+1)} \rangle \\ \langle l_{2(i+1)}, h_{2(i+1)} \rangle \end{bmatrix} = \begin{bmatrix} \langle l_{1i} \sqcup 0 \sqcup min(0, l_{2i}), h_{1i} \sqcup 0 \sqcup max(0, h_{2i}) \rangle \\ \langle l_{2i} \sqcup (l_{1i} \bigoplus 2), h_{2i} \sqcup (h_{1i} \bigoplus 2) \rangle \end{bmatrix} \]

这里可能看不明白，同样我们手推前5项（在第5项就收敛了）。

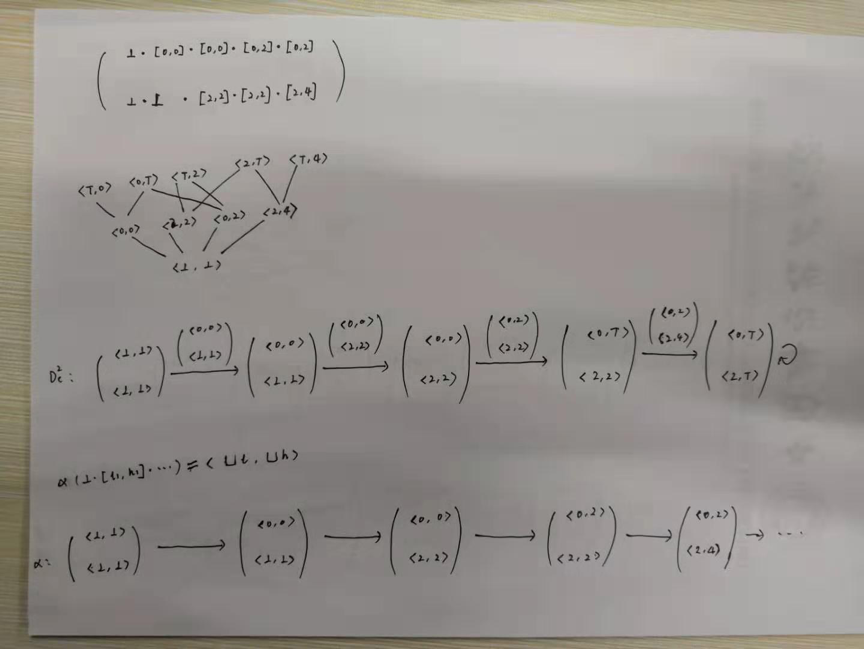
这里看到利用常量传播格 \(D_c\) 的积格（product lattice）\(D_c^2\)，大幅提升了收敛速度。

后面作者举了很多 online/offline \(A^2I\) 的例子，都是一些比较新的静态分析的工作，\(A^2I\) 可以看作是对它们通用的理论上的提炼，一作 Cousot 就是 AI 的提出者。作者指出从 1977 年提出 AI 至今，软件的规模、复杂性不断上升，很多软件也并不是安全攸关的（safety-critical），希望这一框架可以使传统抽象解释步入现代，指导高效精确的程序分析算法设计。