最大子数组01
题目:返回一个整数数组中最大子数组的和
要求:
1.输入一个整形数组,数组里有正数也有负数
2.数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和
3.求所有子数组的和的最大值,要求时间复杂度为O(n)
程序设计思路:
初始时,程序的设计思路为求出整形数组中每个子数组的和,然后通过比较大小的方式,求出最大子数组,但是这样的做法不符合时间复杂度的要求。所以改进思路,采用动态规划的方式解决这个问题。
动态规划求解最大子数组的过程如下:利用迭代的思想,首先求出前i-1个元素的最大子数组,若前i-1个元素的最大子数组的和小于零,则将其抛弃,从第i个元素重新开始记录最大子数组的问题,因为无论第i个元素是正是负,加上前i-1个元素最大值这个负值,结果一定比本身小,所以将前i-1个元素的最大子数组值抛弃,但若第i个元素的值小于最大子数组的值,则应最大子数组的起始位置回复到原来。若第i-1个元素的最大子数组值大于零,则将第i个元素加入其中,然后判断临时值与最大子数组的值大小,如果临时值(即加入第i个元素后的值)比最大子数组值大,则将当下的临时值赋给最大子数组值,并将最大子数组的结束位置设置到当下,即第i个元素。
程序编写过程中出现的问题:
第一次编写成功后,在运行时出现了一个问题,例如有两个元素-1和-9,按照程序的思路,-1小于0,则将最大子数组的起始位置设置到-9,但是-9小于-1,所以最大子数组还是-1,因此,最后输出最大子数组时产生了错误。
解决办法:
我的解决办法就是加了一个判断条件,即如果第i个元素被设置为最大子数组的起始位置后,判断第i个元素和最大子数组值的大小,如果第i个元素的值小于最大子数组值,则将最大子数组的起始位置恢复到原来的起始位置。
程序源代码如下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 | //动态规划求最大子数组问题//2016-03-23#include<iostream>using namespace std;int main(){ int length; //记录数组的长度 cout << "请输入一个一维输入的长度:"; cin >> length; //输入数组长度 while (length < 1) //判断输入是否合法 { cout << "数组长度输入错误,请重新输入:"; cin >> length; } int A[100]; //存放数组长度,如果数组长度不确定,则可用动态申请内存空间的方法 int maxSubSum; //记录最大子数组的和 int start=0, end=0; //初始时设置第一个元素为最大子数组,start和end表示最大子数组的开始和结束 cout << "请输入" << length << "个数组元素:"; for (int i = 0; i < length; i++) { cin >> A[i]; //输入数组的元素 } maxSubSum = A[0]; //将第一个元素的值给最大值进行初始化 int temp = A[0]; //临时记录当前最大值 for (int i = 1; i < length; i++) { if (temp<0) //如果前i个元素的最大子数组值小于零,则将其抛弃,从第i个元素重新开始 { temp = A[i]; int back = start; start = i; if (temp < maxSubSum) //如果临时值比最大值小,则将最大子数组的起始点恢复到原来值 { start = back; } } else //否则将第i个元素也加入到最大子数组中去 { temp = temp + A[i]; } if (maxSubSum < temp) //如果当前值比最大值大,则将当前值赋给最大子数组和 { maxSubSum = temp; end = i; } } cout << "最大子数组为:"; for (int i = 0; i < (end - start+1); i++) { cout << A[start + i] << " "; //输出连续的最大子数组 } cout << endl; cout << "最大子数组的和为:" << maxSubSum << endl; //输出最大子数组的和 return 0;} |
程序运行结果截图如下所示:
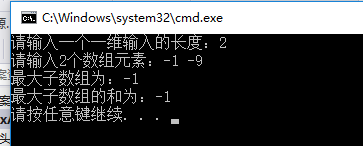
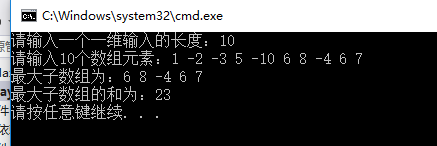
总结:
动态规划求解最大子数组问题非常方便简捷,而且时间复杂度控制在了O(n)中,这比全部求出子数组的和再求最大子数组高效很多,这次实验也让我明白一个优良的算法对于程序的重要性。在后续的学习中,我要努力深入的学习算法的优越性,在以后的工作和编程中,也应该多多留意,多多考虑,尝试用最优化的方式解决实际问题。



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步