[USACO10MAR] Great Cow Gathering G

[USACO10MAR] Great Cow Gathering G

题目描述

\(Bessie\) 正在计划一年一度的奶牛大集会，来自全国各地的奶牛将来参加这一次集会。当然，她会选择最方便的地点来举办这次集会。

每个奶牛居住在 \(N\) 个农场中的一个，这些农场由 \(N-1\) 条道路连接，并且从任意一个农场都能够到达另外一个农场。道路 \(i\) 连接农场 \(A_i\) 和 \(B_i\)，长度为 \(L_i\)。集会可以在 \(N\) 个农场中的任意一个举行。另外，每个牛棚中居住着 \(C_i\) 只奶牛。

在选择集会的地点的时候，\(Bessie\) 希望最大化方便的程度（也就是最小化不方便程度）。比如选择第 \(X\) 个农场作为集会地点，它的不方便程度是其它牛棚中每只奶牛去参加集会所走的路程之和（比如，农场 \(i\) 到达农场 \(X\) 的距离是 \(20\)，那么总路程就是 \(C_i\times 20\)）。帮助 \(Bessie\) 找出最方便的地点来举行大集会。

输入格式

第一行一个整数 \(N\) 。

第二到 \(N+1\) 行：第 \(i+1\) 行有一个整数 \(C_i\)。

第 \(N+2\) 行到 \(2N\) 行：第 \(i+N+1\) 行为 \(3\) 个整数：\(A_i,B_i\) 和 \(L_i\)。

输出格式

一行一个整数，表示最小的不方便值。

提示

\(1\leq N\leq 10^5\)，\(1\leq A_i\leq B_i\leq N\)，\(0 \leq C_i,L_i \leq 10^3\)。

思路

一眼树形\(DP\)。

由于不确定以哪个点为中心，所以先以一个点为根，\(DP\) 后换根，统计最小值。

第一遍 \(DP\) 时，定义 \(dp1[i]\) 表示 \(i\) 的子树中的所有点到 \(i\) 的“不方便程度”之和，\(sum[i]\) 表示 \(i\) 的子树中的所有点的权值之和，那么：

\[dp1[u]=\sum dp1[v]+len(u,v)\times sum[v] \]

因为要从 \(u\) 的儿子节点 \(v\) 转移到 \(u\)，所增加的路程是 \(u\) 到 \(v\) 的距离，所以增加的“不方便程度”是以 \(v\) 为根的子树的权值之和乘上 \(u\) 到 \(v\) 的距离，而每一棵子树的“不方便程度”都会累加到 \(u\) 上，所以会有如上式子。

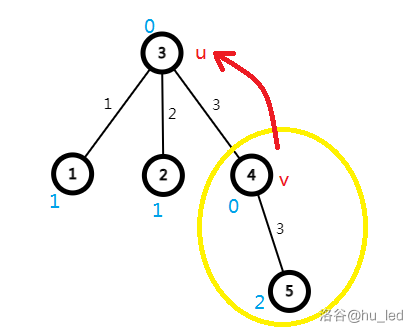
这样求出来的 \(dp1\) 是以特定的某个点为中心的“不方便程度”，并不一定是最终答案，所以我们再 \(dfs\) 一遍，每次求出以当前节点为中心的答案，答案取所有的最小值即可。

所以要怎么求以当前点为中心的答案呢？设 \(dp2\) 表示以 \(i\) 为中心的“不方便程度”，在\(dfs\)的时候，假设已经求出了当前点的父节点的 \(dp2\) 的值，需要转移到当前点。对当前点的答案产生贡献的有两部分：以当前节点为根的子树和整棵树除开子树的其他部分。这两部分贡献的和就是答案。

设当前节点为 \(st\) ，父节点为 \(fa\) 。第一部分的贡献其实就是 \(dp1[st]\) 。第二部分的贡献是 （除开该子树外的其他所有节点对 \(fa\) 的贡献）\(+\) （\(fa\) 到 \(st\) 的距离）\(\times\)（除开该子树外的其他所有节点的权值之和），即：

\[\begin{aligned} dp2[st] &= dp1[st]+(dp2[fa]-dp1[st]-len(fa,st)\times sum[st])+len(fa,st)\times(sum[1]-sum[st])\\ &= dp2[fa]+len(fa,st)\times(sum[1]-2sum[st]) \end{aligned} \]

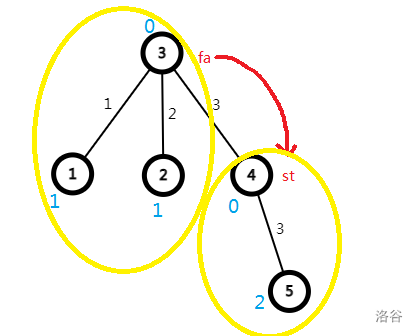
利用如上 \(dp\) 式，通过两次 \(dfs\)（两次\(DP\)）就可以得到答案。

另：注意开 \(long\) \(long\)

代码

#include<bits/stdc++.h>
#define MAXN 100010
#define int long long
#define INF 2000000000
using namespace std;
int n,c[MAXN],x,y,z,start=0,dp1[MAXN],dp2[MAXN],sum[MAXN],ans=INF;
struct edge
{
    int r,w;
};
vector<edge> tmap[MAXN];
int dfs1(int st,int fa)
{
    int ret=c[st],tool;
    sum[st]=c[st];
    for(auto i:tmap[st])
    {
        if(i.r==fa)continue;
        tool=dfs1(i.r,st);
        ret+=tool;
        sum[st]+=sum[i.r];
        dp1[st]+=(dp1[i.r]+tool*i.w);
    }
    return ret;
}
void dfs2(int st,int fa,int last)
{

    if(fa)dp2[st]=dp2[fa]+(sum[1]-sum[st]*2)*last;
    ans=min(ans,dp2[st]);
    for(auto i:tmap[st])
    {
        if(i.r==fa)continue;
        dfs2(i.r,st,i.w);
    }
}
signed main()
{
    scanf("%lld",&n);
    for(int i=1;i<=n;i++)
        scanf("%lld",&c[i]);
    for(int i=1;i<n;i++)
    {
        scanf("%lld%lld%lld",&x,&y,&z);
        tmap[x].push_back(edge{y,z});
        tmap[y].push_back(edge{x,z});
    }
    dfs1(1,1);
    ans=dp2[1]=dp1[1];
    dfs2(1,0,0);
    printf("%lld",ans);
    return 0;
}