洪水题解
【洪水】题解
题目大意
有\(n\)个水库，每个水库有一个容量上限\(a_i\)，第\(i\)个水库到第\(i+1\)个水库有一个流量上限\(b_i\)，最后一个水库流入大海。且每秒会有\(F\)流入第\(1\)个水库，问水库多久会溢出，不会溢出输出\(-1\)
对于n小于4的数据，直接模拟即可
对于所有水库容量相同，河道一样宽的数据
因为所有水库都相同，所以除第一个水库外，其余水库都是水流进来多少就流出去多少，不需要蓄水
所以当前答案就是\(\frac{a_1}{F-b_1}\)
如果\(F\le b_1\)，输出\(-1\)
满分做法
考虑贪心
我们肯定是要让尽可能多的水往后流，这点是非常清楚的
而且水库溢出的条件其实就只有第一个水库溢出（为什么下面讲）
如果第\(1\)个水库没有满，那么我们就可以一直装到满为止。
如果中间有个水库已经满了，我们就可以减少流向这个水库的水，将多余的水存在前面的水库，直至第一个水库
这么一来，我们就得到了一种比较优秀的做法
-
我们先算出每个水库群的净流入(因为越到后面流量肯定是单调不升的，其实就是个前缀最小值)
-
然后我们找到第一个满的水库群\(i\)，将其净流入全部存入\(i-1\)个水库群（就是让第\(i-1\)个水库群的净流量\(+\)第\(i\)个水库群的净流量，一直这样到\(1\)号水库群为止）
这里的净流入和水库群的定义是这样的
水库群:有多个连续的水库组成，这几个水库里的水基本可以任意分配
要怎么样才能满足水库群?
设流入这个水库群的流量为\(F\)，往右找到第一个流量\(<F\)的水库，这些水库就是一个水库群
我们计入水库群的容量为水库群中所有水库容量之和，净流入为这个水库群的总流入-总流出
净流入:水库群中自然状况下每秒必须流入的水量
画张图
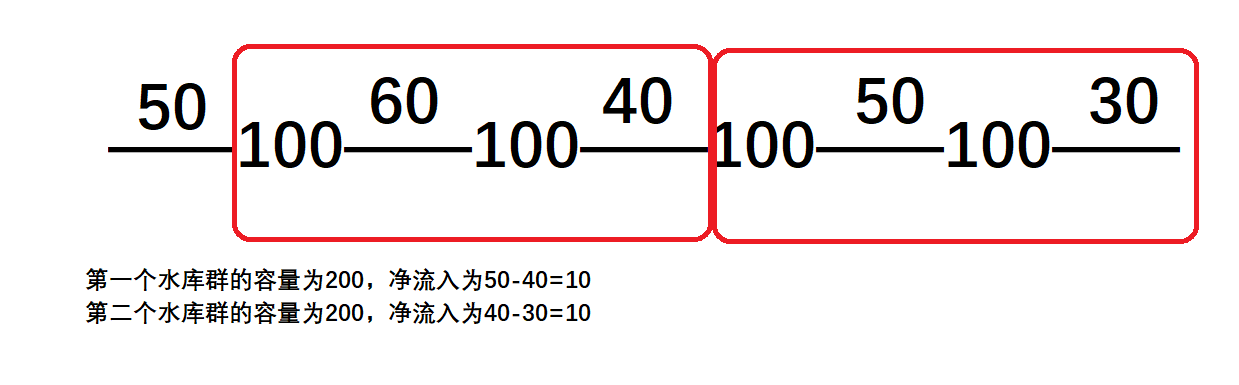
显然，当这些水库中没有任何一个水库群时，那么水便可以一直从头流到尾，输出\(-1\)
显然，当一个水库群满时，我们需要将此水库群的净流入修改为\(0\)
那么每秒消失的水去哪里了呢？我们将前一个水库群的净流入\(+=\)这个水库的净流入，就是要让前一个水库群帮这个水库群分担压力
直到第一个水库群，没有所谓的前一个水库群，此时水库终于溢出
如此，此题完结
#include <bits/stdc++.h>
#define int long long
using namespace std ;
const int MAXN = 3e5 + 5 ;
int n , F ;
int a[ MAXN ] , b[ MAXN ] ;
int sum[ MAXN ] , t[ MAXN ] , tot = 1 ; // 水库群的容量，净流入和水库群的数量
inline int read () {
int tot = 0 , f = 1 ; char c = getchar () ;
while ( c < '0' || c > '9' ) { if ( c == '-' ) f = -1 ; c = getchar () ; }
while ( c >= '0' && c <= '9' ) { tot = tot * 10 + c - '0' ; c = getchar () ; }
return tot * f ;
}
signed main () {
// freopen ( "ex_flood2.in" , "r" , stdin ) ;
// freopen ( "B.out" , "w" , stdout ) ;
n = read () ; F = read () ;
for ( int i = 1 ; i <= n ; i ++ )
a[ i ] = read () ;
for ( int i = 1 ; i <= n ; i ++ )
b[ i ] = read () ;
for ( int i = 1 ; i <= n ; i ++ ) {
if ( b[ i ] < F ) { //前缀最小值，当前的流量
// cout << F - b[ i ] << endl ;
t[ tot ] = F - b[ i ] ; sum[ tot ++ ] += a[ i ] ; F = b[ i ] ; //计算净流入
}
else sum[ tot ] += a[ i ] ;//水库群容量上升
} tot -- ;
if ( tot == 0 ) { //没有任何一个水库群
printf ( "-1\n" ) ;
return 0 ;
}
int pos ;
// cout << pos << endl ;
double ans = 0 ;
while ( 1 ) {
double minx = 9999999999999 ;
for ( int i = 1 ; i <= tot ; i ++ ) {
if ( t[ i ] == 0 ) continue ;//防止除0而RE
if ( minx > (double) sum[ i ] / (double) t[ i ] ) { //找到第一个溢出的水库群
minx = (double) sum[ i ] / (double) t[ i ] ;
pos = i ;//记录下标
}
}
for ( int i = 1 ; i <= n ; i ++ ) sum[ i ] -= t[ i ] * minx ; //因为这个水库群装满需要minx秒，所以其他水库群的容量也要减少
ans += minx ;//记录答案
if ( pos == 1 ) break ; //做到第一个水库就不能往前继续推了
// cout << ans << " " << pos << endl ;
t[ pos - 1 ] += t[ pos ] ;//分担压力
t[ pos ] = 0 ;//净流量降为0
}
printf ( "%.3lf\n" , ans ) ;
return 0 ;
}
感觉这题还能用二分答案+乱搞秒掉，有兴趣的可以试试看
