狄利克雷卷积 & 莫比乌斯反演
积性函数与完全积性函数
积性函数
若一个数论函数\(f\)满足当\(gcd(n,m)=1\)时,\(f(nm)=f(n)f(m)\)
则称\(f\)为积性函数
一些常见的积性函数
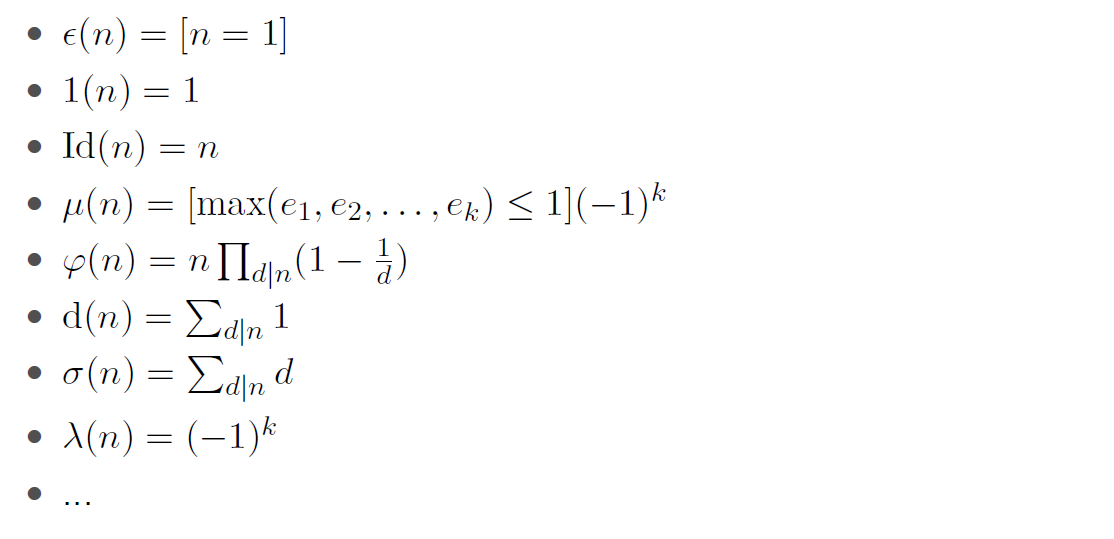
完全积性函数
若一个积性函数函数\(f\)满足当\(gcd(n,m)\ne1\)时,也有\(f(nm)=f(n)f(m)\)
则称\(f\)为完全积性函数
狄利克雷卷积
定义两个数论函数的狄利克雷卷积\(*\)
若\(t=f*g\)
\[t(n)=\sum\limits_{i|n}f(i)g(\frac{n}{i})
\]
等价于
\[t(n)=\sum\limits_{ij=n}f(i)g(j)
\]
狄利克雷卷积有以下性质(两个数论函数相等,是指两个函数的每一项都相等):
- 交换律 \(f*g=g*f\)
- 结合律 \(f*(g*h)=(f*g)*h\)
- 分配律 \(f*h+g*h=(f+g)*h\)
- 没有名字\((xf)*g=x(f*g)\)
- 单位元\(\epsilon*f=f\) ,其中\(\epsilon(n)=[n==1]\)
- 逆元:对于每一个\(f(1)≠0\)的函数\(f\),都有\(f∗g=ϵ\)
讨论一下第六个结论,如何求一个函数的逆呢?
只需要定义
\[g(n)=\frac{1}{f(1)}\left([n==1]-\sum\limits_{i|n,i\ne1}f(i)g(\frac{n}{i})\right)
\]
这样的话
\[\sum\limits_{i|n}f(i)g(\frac{n}{i})=f(1)g(n)+\sum\limits_{i|n,i\ne1}f(i)g(\frac{n}{i})=[n==1]
\]
几种比较常见的卷积关系:
\(\mu*1=\epsilon\) 【莫比乌斯反演】【\(\mu\)与\(1\)互为逆元】
\(\varphi*1=Id\)
\(\varphi=Id*\mu\)
\(d=1*1\)
\(1=\mu*d\)
莫比乌斯反演
我们定义\(1\)的逆是\(\mu\)
这样的话,如果\(g=f∗1\),就有\(f=f∗1∗\mu=g∗\mu\)
换句话说,就是
\[g(n)=\sum\limits_{d|n}f(d)\Leftrightarrow f(n)=\sum\limits_{d|n}\mu(\frac{n}{d})g(d)
\]
也可以这样子
\[g(d)=\sum\limits_{d|n}f(n)\Leftrightarrow f(d)=\sum\limits_{d|n}\mu(\frac{n}{d})*g(n)
\]
例子
怎么用呢?举几个例子(以下情况默认\(n≤m\))
Eg1
求
\[\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}[gcd(i,j)==1]
\]
设
\[f(x)=\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}[gcd(i,j)==1]
\]
\[g(x)=\sum\limits_{x|d}f(d)
\]
则
\[f(1)=\sum_{1|d}\mu(\frac{d}{1})g(d) \\
f(1)=\sum_{i=1}^n\mu(i)g(i)
\]
考虑\(g(x)\)是什么
\[g(x)=\sum_{x|d}\sum_{i=1}^n\sum_{i=1}^m[gcd(i,j)==d]
\]
即
\[g(x)=\sum_{i=1}^n\sum_{i=1}^m[x|gcd(i,j)] \\
g(x)=\sum_{i=1}^{\left\lfloor\frac nx\right\rfloor}\sum_{i=1}^{\left\lfloor\frac mx\right\rfloor}[1|gcd(i,j)]\\
g(x)=\left\lfloor\frac nx\right\rfloor\left\lfloor\frac mx\right\rfloor\]
带回\(f(1)\)
\[Ans=\sum_{x=1}^n\mu(x)\left\lfloor\frac nx\right\rfloor\left\lfloor\frac mx\right\rfloor
\]
这个用整除分块可以做到\(O(\sqrt(n))\)


