算法浅谈之斜率优化
尝试拿一道例题(玩具装箱)来讲明白斜率优化。
-
1） 题目大意
有\(n\)个物品，每个物品有一个体积\(c_i\)，你可以制作无限个箱子，假设你制作的箱子长度为\(x\)，那么你所需花费的费用就是\((x-L)^2\)，现在要求出把\(n\)个物品都放入箱子里的最小费用。
-
2) 普通DP
由题意我们很快就可以得出一个DP式：
\[f_i=min(f_j+(s_i-s_j+i-j-1-L)^2)
\]
暴力求\(f_i\)时间复杂度\(O(n^2)\)
-
3) 斜率优化
我们观察式子，把\(min\)去掉，式子变成
\[f_i=f_j+(s_i-s_j+i-j-1-L)^2
\]
我们把固定的设为\(A(i)\)，不定的设为\(B(i)\)(与\(j\)有关的算不固定值，其余算固定值)
那么
\[A(i)=s_i+i-1-L
\]
\[B(i)=s_i+i
\]
原式变为
\[f_i=f_j+(A(i)-B(j))^2
\]
展开
\[f_i=f_j+A(i)^2+B(j)^2-2A(i)B(j)
\]
移项
\[B(j)^2+f_j=2A(i)B(j)-A(i)^2+f_i
\]
因为斜率优化与\(y,k,x\)有关,由于\(-A(i)^2+f_i\)是常数，所以可以省略
原式就变成了
\[B(j)^2+f_j=2A(i)B(j)
\]
\(y=kx\)
\(B(j)^2+f_j\)为\(y\)
\(2A(i)\)为\(k\)
\(B(j)\)为\(x\)
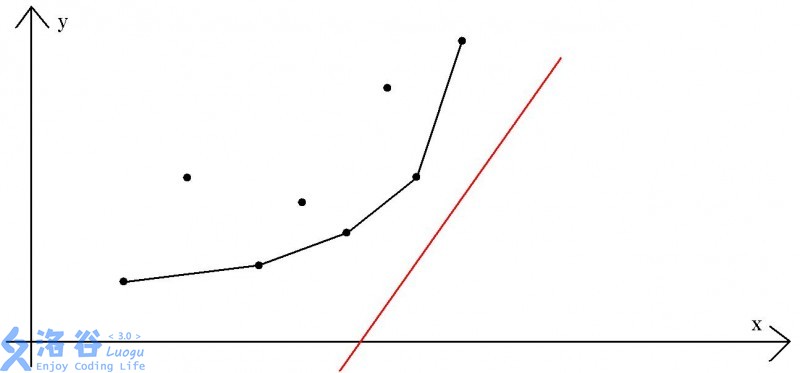
因为\(2A(i)\)为正数，所以整个函数单调递增，因此我们使用单调队列维护下凸包。
#include <bits/stdc++.h>
#define int long long
using namespace std ;
const int MAXN = 5e4 + 5 ;
int n , L ;
int f[ MAXN ] , q[ MAXN ] , l = 1 , r = 0 , sum[ MAXN ] ;
inline int A ( int p ) { return p + sum[ p ] - 1 - L ; }
inline int B ( int p ) { return sum[ p ] + p ; }
inline int X ( int p ) { return B ( p ) ; }
inline int Y ( int p ) { return f[ p ] + B ( p ) * B ( p ) ; }
inline int K ( int p ) { return 2 * A ( p ) ; }
inline int read () {
int tot = 0 , f = 1 ;
char c = getchar () ;
while ( c < '0' || c > '9' ) {
if ( c == '-' ) f = -1 ;
c = getchar () ;
}
while ( c >= '0' && c <= '9' ) {
tot = ( tot << 1 ) + ( tot << 3 ) + ( c ^ 48 ) ;
c = getchar () ;
}
return tot * f ;
}
signed main () {
n = read () ; L = read () ;
for ( int i = 1 ; i <= n ; i ++ ) sum[ i ] = sum[ i - 1 ] + read () ;
q[ ++ r ] = 0 ;
for ( int i = 1 ; i <= n ; i ++ ) {
while ( l < r && K ( i ) * ( X ( q[ l + 1 ] ) - X ( q[ l ] ) ) >= Y ( q[ l + 1 ] ) - Y ( q[ l ] ) ) l ++ ; // 弹出决策点
int p = q[ l ] ;
f[ i ] = f[ p ] + ( A ( i ) - B ( p ) ) * ( A ( i ) - B ( p ) ) ;
while ( l < r && ( ( Y ( i ) - Y ( q[ r ] ) ) * ( X ( q[ r ] ) - X ( q[ r - 1 ] ) ) <= ( X ( i ) - X ( q[ r ] ) ) * ( Y ( q[ r ] ) - Y ( q[ r - 1 ] ) ) ) ) r -- ; // 删除不必要的决策点（上凸点）
q[ ++ r ] = i ;
}
cout << f[ n ] << endl ;
return 0 ;
}
