算法详解之缩点
若图片出问题请转至[这儿]
前置技能:tarjan求强连通分量
缩点。
顾名思义,就是在图论算法中将一些点缩成一个点的一种算法。
- 应用
貌似明白了,但是这有什么用呢?
我们经常求最短路,但是如果我们要求最长路呢?
标准问法:
给你一张有向图,每个点都有一个点权(不是边权了哦),且每一个点都可以经过任意多次,但是点权只能加一次,求这张图的最大权值
题目分析:
看到这,相信大多数人都会想到把最短路的模板改一下就行了,但是这会出问题,你会在一个圈里团团转。
怎么办办?
我们会发现,只要是一堆可以构成强连通分量的点,我们就可以将它们缩成一个点,而这个点的点权就是它们的点权和,它的入边就是它们所有点的入边,出边就是它们所有点的出边。
放几张图有助于理解:
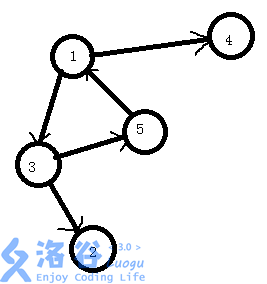
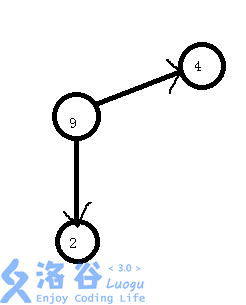
上图中1.3.5就是一个强连通分量
- 怎么实现?
我们在tarjan求强连通分量时开过一个数组叫做color[](或其他名字)来记录一个点 所属于的强连通分量编号。所以我们可以遍历每一个点,看看它所能到达的点是否和它同处于同一个强连通分量中,若不是,则依托它们强连通分量的编号再构建一个有向无环图 (想一想,为什么要依托编号)
- 代码
for(int i=1;i<=n;i++)
{
for(int j=0;j<ver[i].size();j++)
{
int x=ver[i][j];
if(color[i]!=color[x])
{
in[color[x]]++;
g[color[i]].push_back(color[x]);
}
}
}
for(int i=1;i<=n;i++)
ww[color[i]]+=w[i];//点权处理
这样我们就实现了缩点。
- 题目:

