实战--利用HierarchicalClustering 进行基因表达聚类分析
利用建立分级树对酵母基因表达数据进行聚类分析
一、原理
根据基因表达数据,得出距离矩阵

↓
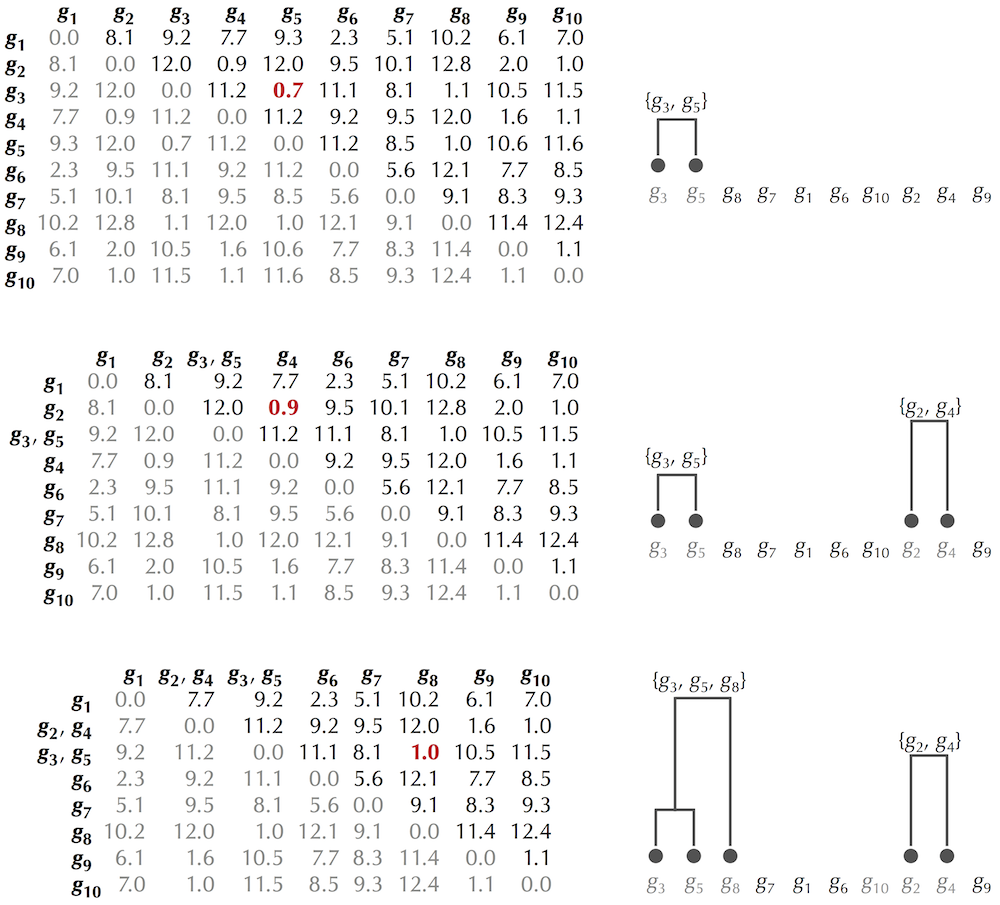
- 最初,每个点都是一个集合
- 每次选取距离最小的两个集合,将他们合并,然后更新这个新集合与其它点的距离
- 新集合与别的集合距离的计算方法
- ①两个集合之间的最短距离
- ②两个集合所有点之间求距离求平均 →
![]()
- 把这个新集合加入距离矩阵中,原来的两个小集合就被替换掉
- 如此循环,直到剩下一个集合,那就建立了一棵树
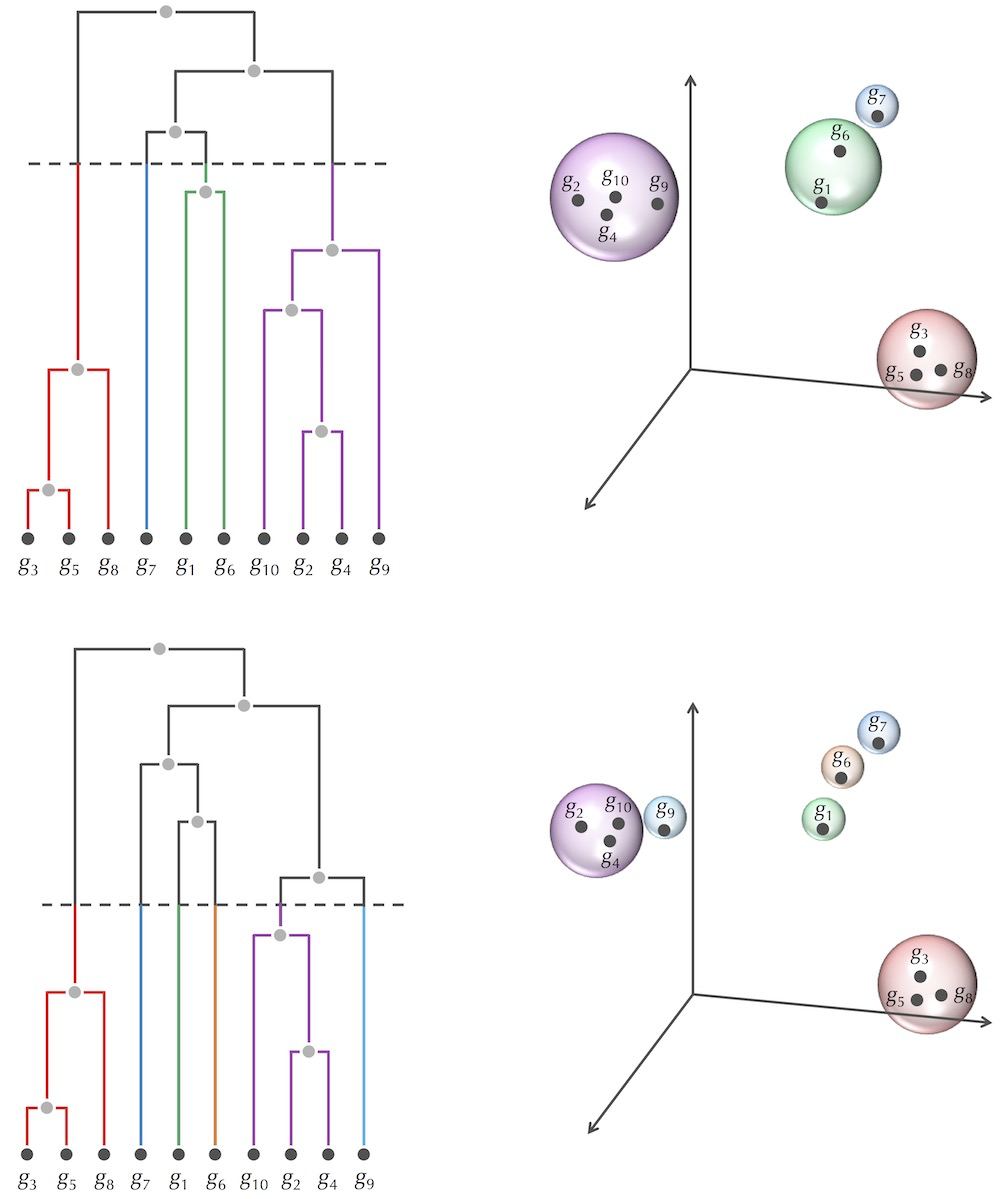
- 在树的某一处横断,就可以得到6类
230个酵母基因表达数据
http://bioinformaticsalgorithms.com/data/realdatasets/Clustering/230genes_log_expression.txt
二、python下利用Sklearn包实现
Sklearn包的安装
参照 https://scikit-learn.org/stable/install.html
代码(python 3.7环境)
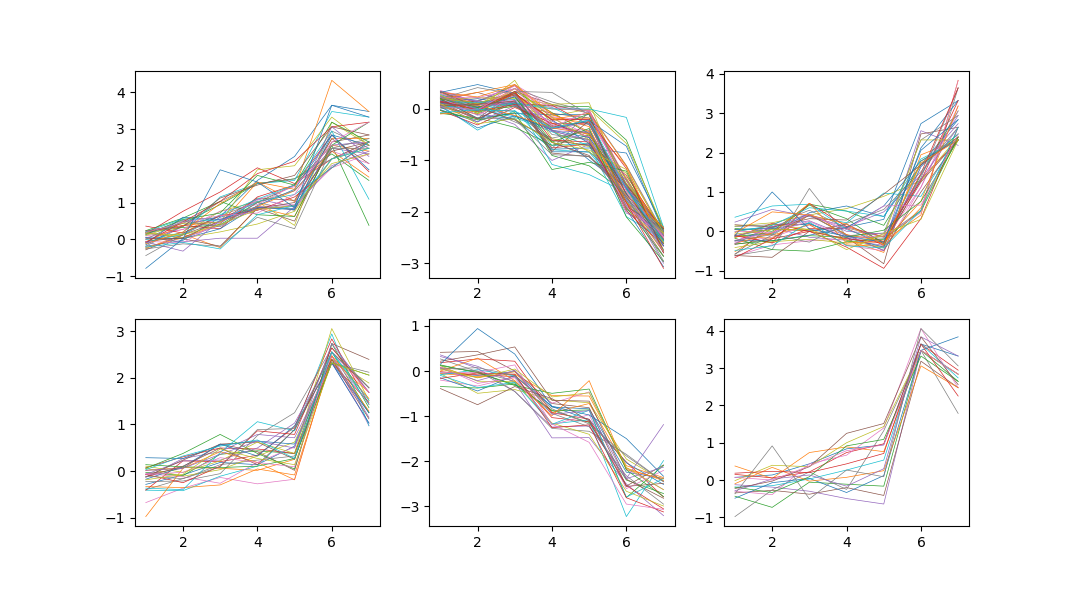
from sklearn.cluster import AgglomerativeClustering import numpy as np from os.path import dirname import numpy as np import math import random import matplotlib.pyplot as plt def InputData(dataset): dataset = [line.split() for line in dataset] name = [item[1] for item in dataset[1:]] points = [] for line in dataset[1:]: if(len(line)==10): points.append(list(map(float,line[3:]))) elif(len(line)==9): points.append(list(map(float,line[2:]))) return points if __name__ == '__main__': f = open("output","w") INF = 999999 dataset = open(dirname(__file__)+'230genes_log_expression.txt').read().strip().split('\n') X = np.array(InputData(dataset)) clustering = AgglomerativeClustering(n_clusters=6).fit(X) #print(clustering.labels_) lb = clustering.labels_ clusters = [[] for i in range(6)] for i in range(len(X)): clusters[lb[i]].append(i) fig=plt.figure() x = [i for i in range(1,8)] for c in range(6): plt.subplot(231+c) for i in clusters[c]: plt.plot(x,X[i],linewidth=0.5,linestyle='-',marker='') plt.show()
结果
!注意
初次使用sklearn的时候python3.7解释器会报错
/Library/Frameworks/Python.framework/Versions/3.7/lib/python3.7/site-packages/sklearn/externals/joblib/externals/cloudpickle/cloudpickle.py:47: DeprecationWarning: the imp module is deprecated in favour of importlib; see the module's documentation for alternative uses import imp
是因为从python3.4开始就不再支持 import imp , 需要按照错误信息找到相关的文件,将import imp 改为 import importlib,问题即解决
三、手动实现建立 Hierarchical树
1 ''' 2 coder Lokwongho 2018.11 3 4 ''' 5 6 from os.path import dirname 7 import numpy as np 8 import math 9 import random 10 import matplotlib.pyplot as plt 11 12 ######## Get the Distance Matrix ######## 13 def PearsonCorrelationDistance(Expres): 14 n = len(Expres) 15 l = len(Expres[0]) 16 Distance = np.zeros(shape=[n,n],dtype=float) 17 18 u = [ sum(i)/l for i in Expres ] 19 Sigma = [] 20 for i in range(n): 21 sig=0; 22 for x in range(l): 23 sig += (Expres[i][x]-u[i])**2; 24 Sigma.append(sig) 25 26 for i in range(n): 27 for j in range(i,n): 28 sigU=0 29 for x in range(l): 30 sigU += (Expres[i][x]-u[i])*(Expres[j][x]-u[j]) 31 Distance[i][j]=1-(sigU)/math.sqrt(Sigma[i]*Sigma[j]) 32 Distance[j][i]=Distance[i][j] 33 34 return Distance 35 36 ######## Build the Hierarchical Tree ######## 37 def locateMin(size): # calculate the diatance between two cluster: minimum distance method 38 minVal = 999999 39 minId = [-1,-1] 40 for x in range(size): 41 for y in range(size): 42 if x!=y and matrix[x][y]<minVal and delete[x]==False and delete[y]==False: 43 minVal = matrix[x][y] 44 minId = [x,y] 45 #print(minId,size) 46 return [minId,minVal] 47 48 def buildTree(): 49 Tree = [[]for i in range(maxn)] 50 global matrix 51 global delete 52 ptr = n 53 delete = [False for i in range(maxn)] 54 num = [0 for i in range(maxn)] 55 for i in range(n): 56 num[i] = 1 57 weight = [0 for i in range(maxn)] 58 while(ptr<maxn): 59 60 [[minX,minY],minVal] = locateMin(ptr) 61 Tree[ptr].append([minX,minVal/2-weight[minX]]) 62 Tree[ptr].append([minY,minVal/2-weight[minY]]) 63 Tree[minX].append([ptr,minVal/2-weight[minX]]) 64 Tree[minY].append([ptr,minVal/2-weight[minY]]) 65 weight[ptr]=minVal/2 66 delete[minX]=True 67 delete[minY]=True 68 #print(minX,minY,minVal) 69 #print(delete) 70 for i in range(ptr+1): 71 if delete[i]==False: 72 tmp=(matrix[minX][i]*num[minX]+matrix[minY][i]*num[minY])/(num[minX]+num[minY]) 73 matrix[ptr][i] = tmp 74 matrix[i][ptr] = tmp 75 num[ptr] = num[minX]+num[minY] 76 ptr += 1 77 return Tree 78 79 def HierarchicalClustering(DMatrix): 80 global maxn 81 global n 82 global Tree 83 global matrix 84 85 86 n = len(DMatrix) 87 maxn = 2*n-1 88 matrix = np.zeros(shape=(maxn,maxn)) 89 for i in range(n): 90 matrix[i][:n] = DMatrix[i] 91 Tree = buildTree() 92 93 ######## Input and output Data ######## 94 def InputData(dataset): 95 dataset = [line.split() for line in dataset] 96 name = [item[1] for item in dataset[1:]] 97 #print(m) 98 # print(m,k) 99 points = [] 100 for line in dataset[1:]: 101 if(len(line)==10): 102 points.append(list(map(float,line[3:]))) 103 elif(len(line)==9): 104 points.append(list(map(float,line[2:]))) 105 return [points,name] 106 107 ''' 108 Reference to 'whoami_T' in csdn for print the tree 109 https://blog.csdn.net/weixin_39722498/article/details/81534247 110 ''' 111 def tree(lst): 112 # 树状图输出列表 113 l = len(lst) 114 if l == 0: 115 print('-' * 3) 116 else: 117 for i, j in enumerate(lst): 118 if i != 0: 119 f.write(tabs[0]) 120 print(tabs[0], end='') 121 if l == 1: 122 s = '=' * 3 123 elif i == 0: 124 s = '┬' + '-' * 2 125 elif i + 1 == l: 126 s = '└' + '─' * 2 127 else: 128 s = '├' + '─' * 2 129 f.write(s) 130 print(s, end='') 131 if isinstance(j, list) or isinstance(j, tuple): 132 if i + 1 == l: 133 tabs[0] += blank[0] * 3 134 else: 135 tabs[0] += '│' + blank[0] * 2 136 tree(j) 137 else: 138 print(name[j]) 139 f.write(name[j] + "\n") 140 tabs[0] = tabs[0][:-3] 141 142 def traversalTree(v): 143 144 global visited 145 if v < n: 146 return [v] 147 visited[v] = 1 148 items = [] 149 for i in Tree[v]: 150 if visited[i[0]] == 0: 151 items += traversalTree(i[0]) 152 153 return [items] 154 155 def outPut(): 156 global visited 157 global tabs 158 global blank 159 160 blank = [ 161 chr(183)] ##此处为空格格式;Windows控制台下可改为chr(12288) ;linux系统中可改为chr(32)【chr(32)==' ' ;chr(183)=='·' ;chr(12288)==' '】 162 tabs = [''] 163 visited = [0 for i in range(maxn)] 164 TreeList = traversalTree(maxn-1) 165 #print(Tree) 166 tree(TreeList) 167 ########################### 168 169 if __name__ == '__main__': 170 171 f = open("output","w") 172 173 INF = 999999 174 dataset = open(dirname(__file__)+'230genes_log_expression.txt').read().strip().split('\n') 175 176 [points,name] = InputData(dataset) 177 178 DMatrix = PearsonCorrelationDistance(points) 179 180 HierarchicalClustering(DMatrix) 181 182 outPut()

===┬--┬--┬--┬--YJL109C ···│··│··│··└──YNL174W ···│··│··└──┬--YLR129w ···│··│·····└──┬--YGR264C ···│··│········└──┬--YLR449W ···│··│···········└──YNL002C ···│··└──┬--┬--YOL039W ···│·····│··└──┬--YNL067W ···│·····│·····└──┬--YDR382W ···│·····│········└──YGL031C ···│·····└──┬--YBR238C ···│········└──┬--YNL065W ···│···········└──┬--YNL303W ···│··············└──┬--┬--┬--YLR249W ···│·················│··│··└──YPL131W ···│·················│··└──┬--┬--YBR032W ···│·················│·····│··└──┬--YNL069C ···│·················│·····│·····└──┬--YBL027W ···│·················│·····│········└──YNL119W ···│·················│·····└──┬--┬--┬--┬--┬--YML063W ···│·················│········│··│··│··│··└──┬--YHL015W ···│·················│········│··│··│··│·····└──YDL136w ···│·················│········│··│··│··└──┬--YLR062C ···│·················│········│··│··│·····└──┬--YLL045c ···│·················│········│··│··│········└──YBR181C ···│·················│········│··│··└──┬--YPL220W ···│·················│········│··│·····└──┬--┬--YDR418W ···│·················│········│··│········│··└──YIL018W ···│·················│········│··│········└──┬--YER131w ···│·················│········│··│···········└──YLR198C ···│·················│········│··└──┬--┬--YGL102C ···│·················│········│·····│··└──YJL190C ···│·················│········│·····└──┬--┬--YBR189W ···│·················│········│········│··└──┬--YJL136C ···│·················│········│········│·····└──YBR191W ···│·················│········│········└──┬--YMR121C ···│·················│········│···········└──┬--YLR076C ···│·················│········│··············└──YLR325C ···│·················│········└──┬--┬--┬--YJR145C ···│·················│···········│··│··└──YLR344W ···│·················│···········│··└──┬--YHL033C ···│·················│···········│·····└──YOL040C ···│·················│···········└──┬--┬--┬--YDR064W ···│·················│··············│··│··└──┬--YHR089C ···│·················│··············│··│·····└──YDL208W ···│·················│··············│··└──┬--YIL069C ···│·················│··············│·····└──┬--YNL096C ···│·················│··············│········└──┬--YOR234C ···│·················│··············│···········└──┬--YDR417C ···│·················│··············│··············└──YGR148C ···│·················│··············└──┬--┬--YKL009W ···│·················│·················│··└──┬--YNL301C ···│·················│·················│·····└──YOL120C ···│·················│·················└──┬--┬--YLR340W ···│·················│····················│··└──┬--YJR123W ···│·················│····················│·····└──YLR048w ···│·················│····················└──┬--┬--YGR214W ···│·················│·······················│··└──YOR309C ···│·················│·······················└──┬--┬--YOR310C ···│·················│··························│··└──YOR312C ···│·················│··························└──┬--YEL054c ···│·················│·····························└──YKR059W ···│·················└──┬--┬--┬--┬--┬--YGL076C ···│····················│··│··│··│··└──YNL175C ···│····················│··│··│··└──┬--YPR137W ···│····················│··│··│·····└──YDL083C ···│····················│··│··└──┬--┬--YJL148W ···│····················│··│·····│··└──┬--YGL078C ···│····················│··│·····│·····└──YAL012W ···│····················│··│·····└──┬--YMR217W ···│····················│··│········└──┬--YGR103W ···│····················│··│···········└──YLR196W ···│····················│··└──┬--YLR186W ···│····················│·····└──┬--YDR025W ···│····················│········└──YBR247C ···│····················└──┬--┬--┬--┬--┬--YHR128W ···│·······················│··│··│··│··└──YKL081W ···│·······················│··│··│··└──┬--┬--YLR180W ···│·······················│··│··│·····│··└──YNL141W ···│·······················│··│··│·····└──┬--YDR060w ···│·······················│··│··│········└──YLR413W ···│·······················│··│··└──┬--┬--┬--YMR290C ···│·······················│··│·····│··│··└──YPL012W ···│·······················│··│·····│··└──┬--YDR144C ···│·······················│··│·····│·····└──YIL053W ···│·······················│··│·····└──┬--┬--YJL177W ···│·······················│··│········│··└──YBR249C ···│·······················│··│········└──┬--YLL044W ···│·······················│··│···········└──YLR448W ···│·······················│··└──┬--┬--YBR048W ···│·······················│·····│··└──YMR131C ···│·······················│·····└──┬--┬--YLR339C ···│·······················│········│··└──YNR053C ···│·······················│········└──┬--YPL226W ···│·······················│···········└──┬--YDR398W ···│·······················│··············└──YAL003W ···│·······················└──┬--YLR355C ···│··························└──┬--YGR160W ···│·····························└──YMR093W ···└──┬--YFR053C ······└──┬--┬--┬--YDL085w ·········│··│··└──┬--YBR117C ·········│··│·····└──┬--┬--YBR116C ·········│··│········│··└──┬--YKL187C ·········│··│········│·····└──YLR267W ·········│··│········└──┬--YDL199c ·········│··│···········└──┬--YBL043W ·········│··│··············└──YBL049W ·········│··└──┬--┬--YBL108W ·········│·····│··└──YCL025C ·········│·····└──┬--┬--YBR051W ·········│········│··└──┬--┬--┬--YNL117W ·········│········│·····│··│··└──YCR010C ·········│········│·····│··└──┬--YER024w ·········│········│·····│·····└──YGR067C ·········│········│·····└──┬--YDL215C ·········│········│········└──┬--YLR377C ·········│········│···········└──┬--YER065c ·········│········│··············└──YKR097W ·········│········└──┬--┬--YLR142w ·········│···········│··└──┬--YIL125W ·········│···········│·····└──┬--YNL195C ·········│···········│········└──┬--YJL089W ·········│···········│···········└──YAL054C ·········│···········└──┬--┬--YJR095W ·········│··············│··└──┬--YOL084W ·········│··············│·····└──┬--YLR174W ·········│··············│········└──┬--YHR096C ·········│··············│···········└──YJL045W ·········│··············└──┬--YEL012w ·········│·················└──┬--YBL045C ·········│····················└──┬--YGL259W ·········│·······················└──YLR312C ·········└──┬--┬--YCR021c ············│··└──┬--YDR343C ············│·····└──┬--YER053c ············│········└──YMR250W ············└──┬--┬--┬--┬--┬--YIL136W ···············│··│··│··│··└──┬--YMR090W ···············│··│··│··│·····└──YNL305C ···············│··│··│··└──┬--┬--YHR087W ···············│··│··│·····│··└──YKL142W ···············│··│··│·····└──┬--YDR031w ···············│··│··│········└──YJR096W ···············│··│··└──┬--YDR516C ···············│··│·····└──YIL111W ···············│··└──┬--┬--YDR342C ···············│·····│··└──YBR183W ···············│·····└──┬--┬--┬--┬--YBR072W ···············│········│··│··│··└──┬--YKL085W ···············│········│··│··│·····└──YLR327C ···············│········│··│··└──┬--┬--YGR008C ···············│········│··│·····│··└──┬--YNL200C ···············│········│··│·····│·····└──┬--YNL173C ···············│········│··│·····│········└──YOL053C ···············│········│··│·····└──┬--YGR248W ···············│········│··│········└──YNL015W ···············│········│··└──┬--YLR258W ···············│········│·····└──┬--YKL103C ···············│········│········└──┬--YGL037C ···············│········│···········└──YLR178C ···············│········└──┬--┬--┬--YHL021C ···············│···········│··│··└──YML128C ···············│···········│··└──┬--YFR015C ···············│···········│·····└──YMR105C ···············│···········└──┬--┬--YFL014W ···············│··············│··└──YOR374W ···············│··············└──┬--YGR244C ···············│·················└──┬--YLL041c ···············│····················└──┬--YER150w ···············│·······················└──YNL160W ···············└──┬--┬--┬--┬--┬--YLL026w ··················│··│··│··│··└──YDR258C ··················│··│··│··└──┬--YDR258C ··················│··│··│·····└──YLR149C ··················│··│··└──┬--┬--YBR139W ··················│··│·····│··└──YLR304C ··················│··│·····└──┬--┬--YEL024w ··················│··│········│··└──┬--YDR529C ··················│··│········│·····└──YPR149W ··················│··│········└──┬--YDR178W ··················│··│···········└──YEL011w ··················│··└──┬--┬--┬--YHR051W ··················│·····│··│··└──┬--YNL052W ··················│·····│··│·····└──YNR001C ··················│·····│··└──┬--YKL141W ··················│·····│·····└──YOR065W ··················│·····└──┬--YBL100C ··················│········└──YPR184W ··················└──┬--┬--YIL162W ·····················│··└──┬--┬--┬--YKL193C ·····················│·····│··│··└──┬--YIL113W ·····················│·····│··│·····└──YMR170C ·····················│·····│··└──┬--┬--YOL032W ·····················│·····│·····│··└──┬--YKL151C ·····················│·····│·····│·····└──┬--YDR272W ·····················│·····│·····│········└──YCL035C ·····················│·····│·····└──┬--YFL054C ·····················│·····│········└──┬--YNL274C ·····················│·····│···········└──┬--YLR270W ·····················│·····│··············└──┬--YDR272W ·····················│·····│·················└──YHR104W ·····················│·····└──┬--YLR356W ·····················│········└──YBR241C ·····················└──┬--YDL204w ························└──┬--┬--┬--YBL015W ···························│··│··└──┬--YKL217W ···························│··│·····└──YMR107W ···························│··└──┬--YMR191W ···························│·····└──┬--YKL109W ···························│········└──YML054C ···························└──┬--YGL191W ······························└──┬--┬--┬--YGR243W ·································│··│··└──┬--YBL048W ·································│··│·····└──YGR236C ·································│··└──┬--YDR070c ·································│·····└──┬--YBR147W ·································│········└──┬--YNL134C ·································│···········└──YNL194C ·································└──┬--┬--┬--YBL064C ····································│··│··└──YGR043C ····································│··└──┬--┬--YDR171W ····································│·····│··└──YBL078C ····································│·····└──┬--YKL026C ····································│········└──┬--YOR215C ····································│···········└──┬--YFR033C ····································│··············└──YGR088W ····································└──┬--YER067w ·······································└──┬--YDR533C ··········································└──YOR178C
posted on 2018-11-18 14:16 iojafekniewg 阅读(2184) 评论(0) 收藏 举报




 浙公网安备 33010602011771号
浙公网安备 33010602011771号