数据结构与算法总结1 排序

排序

1、冒泡排序

核心代码

它的思想就是，每一次遍历，往后面添加一个当前最大的元素

。

63

79

98

void Bubble_Sort( ElementType A[], int N )
{  for ( P=N-1; P>=0; P-- ){
}
flag = 0;
for( i=0; i<P; i++ ) { /* 一趟冒泡 */
} }
if ( A[i] > A[i+1] ) { Swap(A[i], A[i+1]);
flag = 1; /* 标识发生了交换 */
if ( flag==0 ) break; /* 全程无交换 */ }

算法分析

最好情况:顺序T = O( N )

最坏情况:逆序 T = O( N2 ) 

稳定

2、插入排序

#include <iostream>
using namespace std;
int main(int argc, char *argv[]) {
    int a[10] = {7,2,6,1,3,5,9,4,12,51};
    int tmp;
    for(int i=1;i<10;i++){
        tmp = a[i];
        int j;
        for(j=i-1;j>=0;j--){
            if(tmp<a[j]){
                a[j+1] = a[j];
            }else{
                break;
            }
        }
        a[j+1] = tmp;
    }
    for(int i=0;i<10;i++){
        printf("%d ",a[i]);
    }
}

 算法分析：

最好情况:顺序T = O( N )

最坏情况:逆序 T = O( N2 ) 

 

2、希尔排序

#include <iostream>
#include <vector>
using namespace std;
int main(int argc, char *argv[]) {
    int a[11] = {11,7,2,6,1,3,5,9,4,12,51};
    int tmp;
    int D = 11/2;
    for(;D>=1;D/=2){
        for(int i=D;i<11;i+=D){ //??
            tmp = a[i];
            int j;
            for(j=i;j>=D&&tmp<a[j-D];j-=D){
                a[j] = a[j-D];
            }
            a[j] = tmp;
        }
    }
    for(int i=0;i<10;i++){
        printf("%d ",a[i]);
    }
}

定义增量序列DM >DM-1 >...>D1 =1
 对每个 Dk 进行“Dk-间隔”排序( k = M, M-1, ... 1 )

 注意:“Dk-间隔”有序的序列，在执行“Dk-1-间隔”排序后，仍然是“Dk- 间隔”有序的 

 

利用Hibbard增量序列、Sedgewick 增量序列可以避免增量不互质造成的问题

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
int main(int argc, char *argv[]) {
    vector<int> Hibbard;
    int a[11] = {11,7,2,6,1,3,5,9,4,12,51};
    for(int i=1;i<=11;i++){
        Hibbard.push_back(pow(2, i)-1);
        if((pow(2, i)-1)>11/2) break;
    }
    int tmp;
    for(int i=Hibbard.size()-1;i>=0;i--){
        D = Hibbard[i];
        for(int i=D;i<11;i+=D){ //??
            tmp = a[i];
            int j;
            for(j=i;j>=D&&tmp<a[j-D];j-=D){
                a[j] = a[j-D];
            }
            a[j] = tmp;
        }
    }
    for(int i=0;i<10;i++){
        printf("%d ",a[i]);
    }
}

 3、堆排序

 

4、归并排序 分治思想

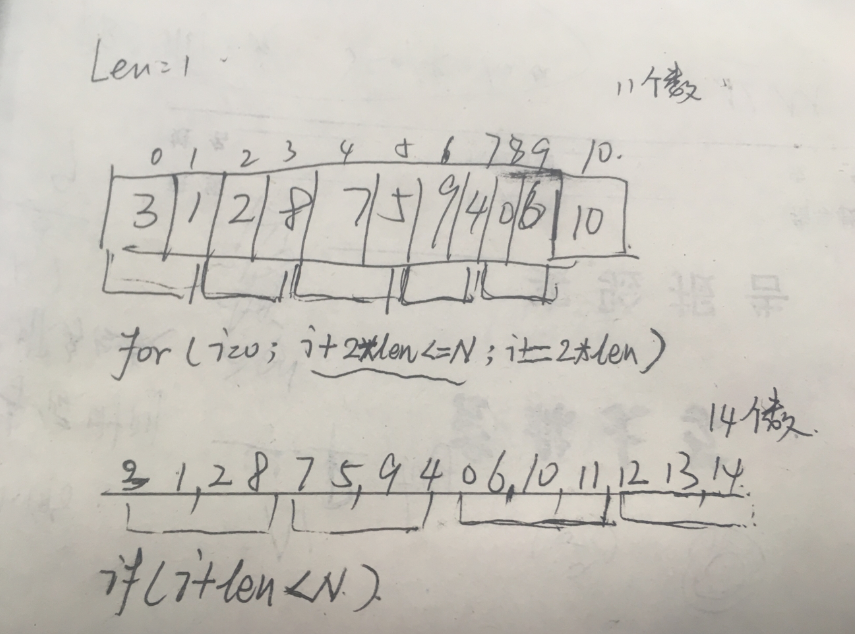
注意点：1、for中的边界 2、len的边界<n

 

void msort(int n,int a[],int tmpa[],int len){
    int i;
    for(i=0;i+len*2<=n;i+=len*2){
        merge(a,tmpa,i,i+len-1,i+len,i+2*len-1);
    }
    if(i+len<n){
        merge(a, tmpa, i, i+len-1, i+len, n-1);
    }else{
        for(;i<n;i++){
            tmpa[i] = a[i];
        }
    }
}

5、快速排序

 

#include <iostream>
using namespace std;
const int maxn = 100006;
int a[maxn];
int cutoff = 2;
int n;

void swap(int i,int j){
    int tmp;
    tmp = a[i];
    a[i] = a[j];
    a[j] = tmp;
}

int Median(int l,int r){
    int c = (l+r)/2;
    int tmp;
    if(a[l]>a[r]){
        swap(l, r);
    }
    if(a[l]>a[c]){
        swap(l, c);
    }
    if(a[c]>a[r]){
        swap(c, r);
    }
    swap(c, r-1);
    return a[r-1];
}



void Insert_sort(int l, int r){
    int tmp;
    for(int i=l+1;i<=r;i++){
        tmp = a[i];
        int j;
        for(j=i-1;j>=0;j--){
            if(a[j]>tmp){
                a[j+1]=a[j];
            }else{
                break;
            }
        }
        a[j+1] = tmp;
    }
}

void QuickSort(int l, int r){
    if(cutoff<=r-l){
        int pivot = Median(l, r);
        //printf("pivot=%d\n",pivot);
        int i=l, j=r-1;
        while(1){
            
            while(a[++i]<pivot);
            while(a[--j]>pivot);
            if(i<j){
                swap(i,j);
            }else{
                break;
            }
        }

        swap(i,r-1);
        QuickSort(l, i-1);
        QuickSort(i+1, r);
    }else{
        Insert_sort(l,r);
    }
}

int main(int argc, char *argv[]) {
     cin >> n;
    for(int i=0;i<n;i++){
        scanf("%d",&a[i]);
    }
    
    QuickSort(0,n-1);
    
    for(int i=0;i<n;i++){
        printf("%d ",a[i]);
    }
}
/*
10
4 2 1 6 7 4 9 10 12 6
*/