[ python ] 递归函数
递归函数
描述:
如果一个函数在内部调用自身本身,这个函数就是递归函数
递归函数特性:
(1)必须有一个明确的结束条件
(2)每次进入更深一层递归时,问题规模相比上次递归都应有所减少
(3)相邻两次重复之间有紧密的联系,前一次要为后一次做准备
(4)递归效率不高,递归层次过多会导致溢出
首先,我们可以从字面上来理解递归函数
递:传递出去的意思
归:回来的意思
递归函数就是一个有去有回的过程,以下一个简单的例子来解释递归函数:
实例:
计算一个10以下(包括10)整数的加法运算:
(1)初级写法:
n = 0
for i in range(11):
n += i
print(n)
(2)中级写法:
使用 reduce 高阶函数进行累计运算
from functools import reduce print(reduce(lambda x, y: x+y, range(11)))
(3)递归函数的写法:
def add(n):
if n == 1:
return n
else:
return n + add(n -1)
print(add(10))
这三种方法,显然第二种是最简单的,但是这里是为了研究递归函数的用法,要了解递归函数的工作流程,就需要分解递归函数。
这里只是为了说明问题,调用 add(5) :
def add(n): # n = 5
if n == 1:
return n
else:
return n + add(n -1) # 5 + add(5 -1)
def add(n): # add(4)
if n == 1:
return n
else:
return n + add(n -1) # 4 + add(4 -1)
def add(n): # add(3)
if n == 1:
return n
else:
return n + add(n -1) # 3 + add(3 -1)
def add(n): # add(2)
if n == 1:
return n
else:
return n + add(n -1) # 2 + add(2 -1)
def add(n): # add(1)
if n == 1: # n = 1
return n # return 1
else:
return n + add(n -1)
以上是我们通过代码执行流程分解出来的过程信息。
每当函数内部调用自身的时候,外部函数挂起,执行内部函数,当内部函数执行完毕,然后在执行外部函数;
用简单的图形来表示,如下:
===> add(5) ===> 5 + add(4) ===> 5 + (4 + add(3)) ===> 5 + (4 + (3 + add(2))) ===> 5 + (4 + (3 + (2 + add(1)))) ===> 5 + (4 + (3 + (2 + 1))) ===> 5 + (4 + (3 + 3)) ===> 5 + (4 + 6) ===> 5 + 10 ===> 15
递归函数的优点是定义简单,逻辑清晰。理论上,所有的递归函数都可以写成循环的方式,但循环的逻辑不如递归清晰。
实例:
使用递归函数实现一个三级菜单的效果

menu = { '北京': { '海淀': { '五道口': { 'soho': {}, '网易': {}, 'google': {} }, '中关村': { '爱奇艺': {}, '汽车之家': {}, 'youku': {}, }, '上地': { '百度': {}, }, }, '昌平': { '沙河': { '北航': {}, }, '天通苑': {}, '回龙观': {}, }, '朝阳': {}, '东城': {}, }, '上海': { '闵行': { "人民广场": { '炸鸡店': {} } }, '闸北': { '火车战': { '携程': {} } }, '浦东': {}, }, '山东': {}, }
提示:在编写递归函数的时候要牢记以下三点:
(1)必须有一个明确的结束条件
(2)当数据按照一定规律执行的时候,才能考虑递归实现
(3)只有调用自身的函数才是递归函数

def treeML(dic): while True: for i in dic: print(i) key = input('>>>').strip() if key == 'q' or key == 'b': return key elif key in dic: res = treeML(dic[key]) if res == 'q': return 'q' treeML(menu)
二分查找算法与递归函数
二分查找算法:
简单来讲,就是一半一半的找。
二份查找实例:
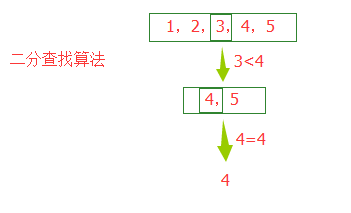
有这样一个数列:
1,2,3,4,5
当我们想要查找数字:4
原始的办法:
从数列中一个一个遍历,直到找到 4 为止,查找了 4 次。
二分查找算法:
首先切一半得到:3,因为 3< 4 我们获取右半边的数列 4, 5
然后我们在切一半得到:4,4=4,在二分算法中,我们一共就找了 2 次就得到结果。
当我们想的多了,总结出更加便捷的方式,计算机才能更加高效的工作;
现在通过递归函数来实现,二分查找算法:
数列:
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
查找序列中是否有数字:83
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
基础实现:
def find(l, aim):
mid_index = len(l) // 2 # 这里需要取整数不能是小数
if l[mid_index] > aim: # 当取的值大于要找的值,取左边
find(l[:mid_index], aim) # 通过切片取list左边的值
elif l[mid_index] < aim: # 当取的值大于要找的值,取右边
find(l[mid_index+1:], aim) # 通过切片取list右边的值
else:
print(mid_index, l[mid_index]) # 数字比较只有三种情况,大于、小于、等于
find(l, 82)
上面的实例,虽然找到序列中含有 82 但是 索引位置是有问题的。修改如下:
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
def find(l, aim, start=None, end=None):
start = start if start else 0
end = len(l) -1 if end is None else end
mid_index = (end - start) // 2 + start
if start > end:
return None
if l[mid_index] > aim:
return find(l, aim, start, mid_index-1)
elif l[mid_index] < aim:
return find(l, aim, mid_index+1, end)
elif l[mid_index] == aim:
return mid_index, l[mid_index]
res = find(l, 82)
print(res)
# 执行结果:
# (22, 82)
以上递归函数,比较疑惑的地方:
end = len(l)-1 if end is None else end
这里为什么:len(l)-1
分析结果如下:
提示:如果要对递归函数进行分析,需要将代码执行流程分解开,查看就更加明显了。
l = [2,3,5]
def find(l, aim, start=None, end=None):
start = start if start else 0 # start = 0
end = len(l) if end is None else end # end = 3
mid_index = (end - start) // 2 + start # mid_index = (3-0) // 2 + 0 =1
if start > end:
return None
if l[mid_index] > aim:
return find(l, aim, start, mid_index-1)
elif l[mid_index] < aim: # 3 < 100
return find(l, aim, mid_index+1, end) # find(l, 6, 2, 3)
elif l[mid_index] == aim:
return mid_index, l[mid_index]
--------------------------------------------------------------------------------------------
通过第一步我们获取到:
find(l, 6, start=2, end=3)
l最大的索引为:2
--------------------------------------------------------------------------------------------
def find(l, aim, start=None, end=None): # find(l, 6, 2, 3)
start = start if start else 0 # start = 2
end = len(l) if end is None else end # end = 3
mid_index = (end - start) // 2 + start # mid_index = (3-2) // 2 + 2 =2
if start > end:
return None
if l[mid_index] > aim:
return find(l, aim, start, mid_index-1)
elif l[mid_index] < aim: # 5 < 6
return find(l, aim, mid_index+1, end) # find(l, 6, 3, 3)
elif l[mid_index] == aim:
return mid_index, l[mid_index]
--------------------------------------------------------------------------------------------
通过第二步我们获取到:
find(l, 6, start=3, end=3)
l最大的索引为:2
--------------------------------------------------------------------------------------------
def find(l, aim, start=None, end=None): # find(l, 6, 3, 3)
start = start if start else 0 # start = 3
end = len(l)-1 if end is None else end # end = 3
mid_index = (end - start) // 2 + start # mid_index = (3-3) // 2 + 3 = 3
if start > end:
return None
if l[mid_index] > aim: # l 最大的索引为:2 这里:l[3] 报错啦,因此 end = len(l)-1 if end is None else end
return find(l, aim, start, mid_index-1)
elif l[mid_index] < aim:
return find(l, aim, mid_index+1, end) # find(l, 6, 3, 3)
elif l[mid_index] == aim:
return mid_index, l[mid_index]
附加题:
使用递归函数求斐波拉契数列.
首先斐波拉契数列如下:
1,1,2,3,5,8
规律:从第三位开始,后面的值是前面两个值的和
def fib(n):
if n == 1 or n == 2:
return 1
return fib(n -1) + fib(n -2)
上面的函数是按照斐波拉契数列规律写出来的,思路是没问题的,但是在函数内部调用两次自身函数,这样的效率非常慢。
因此在使用递归函数时,一定要注意在函数内部只能调用一个,否则严重影响执行效率
上面的递归函数修改如下:
count = 0
def fib(n, a=0, b=1):
# 每次递归获取全局变量count = 0
global count
# 在递归函数中,count = 1
count += 1
# 当 1 < n -1 时,进行函数的递归计算
if count < n-1:
return fib(n, b, a+b)
# 当 1 >= n -1 时,n = 2 或者 n =1 返回 a + b = 0 + 1 = 1
elif count >= n -1:
return a+b
f = fib(10)
print(f)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号