红黑树的插入

一、红黑树的介绍

先来看下算法导论对R-B Tree的介绍：
　　红黑树，一种二叉查找树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。
通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其
他路径长出俩倍，因而是接近平衡的。

　　前面说了，红黑树，是一种二叉查找树，既然是二叉查找树，那么它必满足二叉查找树的一般性质。
下面，在具体介绍红黑树之前，咱们先来了解下 二叉查找树的一般性质：
1.在一棵二叉查找树上，执行查找、插入、删除等操作，的时间复杂度为O（lgn）。
    因为，一棵由n个结点，随机构造的二叉查找树的高度为lgn，所以顺理成章，一般操作的执行时间为O（lgn）。
    至于n个结点的二叉树高度为lgn的证明，可参考算法导论 第12章 二叉查找树 第12.4节。
2.但若是一棵具有n个结点的线性链，则此些操作最坏情况运行时间为O（n）。

 

而红黑树，能保证在最坏情况下，基本的动态几何操作的时间均为O（lgn）。

我们知道，红黑树上每个结点内含五个域，color，key，left，right，p。如果相应的指针域没有，则设为NIL。

一般的，红黑树，满足以下性质，即只有满足以下全部性质的树，我们才称之为红黑树：

1）每个结点要么是红的，要么是黑的。
2）根结点是黑的。
3）每个叶结点，即空结点（NIL）是黑的。
4）如果一个结点是红的，那么它的俩个儿子都是黑的。
5）对每个结点，从该结点到其子孙结点的所有路径上包含相同数目的黑结点。

 

注：实际上考虑的情况有6种，而其中的三种与另外三种是对称的。这取决于下面算法中  p[z] = left[p[p[z]]]这一句。

 

红黑树插入的第一种情况（RB-INSERT-FIXUP(T, z)代码的具体分析一）

为了保证阐述清晰，重述下RB-INSERT-FIXUP(T, z)的源码：

RB-INSERT-FIXUP(T, z)
 1 while color[p[z]] = RED
 2     do if p[z] = left[p[p[z]]]
 3           then y ← right[p[p[z]]]
 4                if color[y] = RED
 5                   then color[p[z]] ← BLACK                    ▹ Case 1
 6                        color[y] ← BLACK                       ▹ Case 1
 7                        color[p[p[z]]] ← RED                   ▹ Case 1
 8                        z ← p[p[z]]                            ▹ Case 1
 9                   else if z = right[p[z]]
10                           then z ← p[z]                       ▹ Case 2
11                                LEFT-ROTATE(T, z)              ▹ Case 2
12                           color[p[z]] ← BLACK                 ▹ Case 3
13                           color[p[p[z]]] ← RED                ▹ Case 3
14                           RIGHT-ROTATE(T, p[p[z]])            ▹ Case 3
15           else (same as then clause
                         with "right" and "left" exchanged)
16 color[root[T]] ← BLACK

 //case1表示情况1，case2表示情况2，case3表示情况3.

咱们，先来透彻分析红黑树插入的第一种情况：

插入情况1，z的叔叔y是红色的。

第一种情况，即上述代码的第5-8行：
 5                   then color[p[z]] ← BLACK                    ▹ Case 1
 6                        color[y] ← BLACK                       ▹ Case 1
 7                        color[p[p[z]]] ← RED                   ▹ Case 1
 8                        z ← p[p[z]]                            ▹ Case 1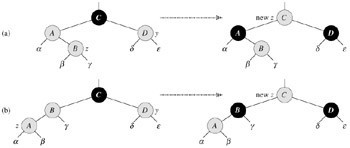

如上图所示，a：z为右孩子，b：z为左孩子。

只有p[z]和y（上图a中A为p[z]，D为z，上图b中，B为p[z]，D为y）都是红色的时候，才会执行此情况1.

咱们分析下上图的a情况，即z为右孩子时

因为p[p[z]]，即c是黑色，所以将p[z]、y都着为黑色（如上图a部分的右边），

此举解决z、p[z]都是红色的问题，将p[p[z]]着为红色，则保持了性质5.

红黑树插入的第二种、第三种情况

插入情况2：z的叔叔y是黑色的，且z是右孩子

插入情况3：z的叔叔y是黑色的，且z是左孩子

这俩种情况，是通过z是p[z]的左孩子，还是右孩子区别的。

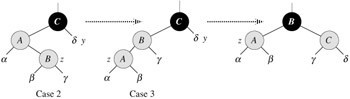
参照上图，针对情况2，z是她父亲的右孩子，则为了保持红黑性质，左旋则变为情况3，此时z为左孩子，

因为z、p[z]都为黑色，所以不违反红黑性质（注，情况3中，z的叔叔y是黑色的，否则此种情况就变成上述情况1 了）。

 我们已经看出来了，情况2，情况3都违反性质4（一个红结点的俩个儿子都是黑色的）。

所以情况2->左旋后->情况3，此时情况3同样违反性质4，所以情况3->右旋，得到上图的最后那部分。

注，情况2、3都只违反性质4，其它的性质1、2、3、5都不违背。

 

下面附上java代码:

 

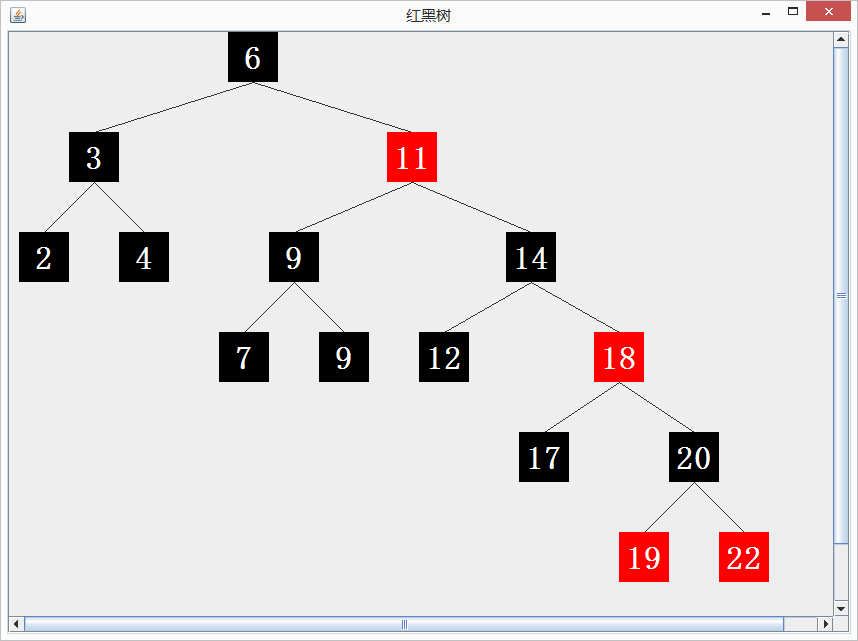
效果图如下：

 

 

 

package com.hjzgg.rbt;

import java.awt.Rectangle;

public class RBTNode {
    public static final boolean RED = true;
    public static final boolean BLACK = false;
    public RBTNode[] child = new RBTNode[2];
    public RBTNode parent;
    public int key;
    public boolean color;
    public RBTNode(RBTNode parent, int key, boolean color) {
        super();
        this.parent = parent;
        this.key = key;
        this.color = color;
        child[0] = child[1] = null;
    }
    
    private int level;//这个节点在树中的层次
    private Rectangle rect;//节点在图形面板中的位置
    public int getLevel() {
        return level;
    }
    public void setLevel(int level) {
        this.level = level;
    }
    public Rectangle getRect() {
        return rect;
    }
    public void setRect(Rectangle rect) {
        this.rect = rect;
    }
    
}

package com.hjzgg.rbt;

import java.awt.BorderLayout;
import java.awt.Color;
import java.awt.Dimension;
import java.awt.Font;
import java.awt.Graphics;
import java.awt.HeadlessException;
import java.awt.Rectangle;
import java.util.ArrayList;
import java.util.LinkedHashMap;
import java.util.Map;

import javax.swing.JFrame;
import javax.swing.JLabel;
import javax.swing.JPanel;
import javax.swing.JScrollPane;

public class RBTGraphic {
    private RBTNode T = null;
    private final int distNode = 50;//节点之间的距离
    private final int heightNode = 50;//节点的高度
    private final int widthNode = 50;//节点的宽度
    private final int levelHeight = 100;//层与层之间的高度
    private ArrayList<Rectangle> line = new ArrayList<Rectangle>();
    private int curY = 0;
    private int curX = 10;
    
    public RBTGraphic(RBTNode T) {
        super();
        this.T = T;
        prepareGraphic();
    }
    
    public class TreeFrame extends JFrame{
        private JPanel panel = new JPanel(){
            @Override
            protected void paintComponent(Graphics g) {
                super.paintComponent(g);
                for(Rectangle rect : line){
                    g.drawLine(rect.x, rect.y, rect.width, rect.height);
                }
            }
        };
        private JScrollPane scrollPane = new JScrollPane(panel);
        public TreeFrame() throws HeadlessException {
            super();
            init();
        }

        public TreeFrame(String title) throws HeadlessException {
            super(title);
            init();
        }
        
        private void init(){
            setLayout(new BorderLayout());
            panel.setLayout(null);
            drawTree(T);
            add(scrollPane, BorderLayout.CENTER);
            int width = curX + 50;
            int height = curY + 50;
            //这里要设置面板的PreferredSize，如果当前Frame大小不能显示PreferredSize那么才会出现滚动条
            panel.setPreferredSize(new Dimension(width, height));
            if(width > 600) width = 600;
            if(height > 300) height = 500;
            setBounds(400, 100, width, height);
            setVisible(true);
        }
        
        public void drawTree(RBTNode o){
            if(o==null) return;
            JLabel label = new JLabel(o.key+"", JLabel.CENTER);
            label.setBounds(o.getRect());
            label.setFont(new Font("宋体",Font.BOLD, 32));
            label.setForeground(Color.WHITE);
            label.setOpaque(true);
            if(o.color == RBTNode.RED)
                label.setBackground(Color.RED);
            else
                label.setBackground(Color.BLACK);
            panel.add(label);
            if(o.child[0]==null && o.child[1]==null) return;
            int x = o.getRect().x+ widthNode/2;
            int y = o.getLevel()*levelHeight+heightNode;
            for(int i=0; i<2; ++i){
                drawTree(o.child[i]);
                if(o.child[i]==null) continue;
                int xx = o.child[i].getRect().x + widthNode/2;
                int yy = y+levelHeight-heightNode;
                line.add(new Rectangle(x, y, xx, yy));
            }
        }
    }
    
    private void prepareNodeLevel(RBTNode o, int level){//确定每一个节点的层次
        if(o==null) return; 
        o.setLevel(level);
        prepareNodeLevel(o.child[0], level+1);
        prepareNodeLevel(o.child[1], level+1);
        if(curY < (level+1)*levelHeight) curY = (level+1)*levelHeight;
    }
    
    private void prepareNodeSize(RBTNode o){//确定节点的坐标位置
        if(o==null) return;
        if(o.child[0]==null && o.child[1]==null){//终结点
            int x = curX; curX+=distNode+widthNode;
            int y = o.getLevel()*levelHeight;
            o.setRect(new Rectangle(x, y, widthNode, heightNode));
            return;
        }
        prepareNodeSize(o.child[0]);
        prepareNodeSize(o.child[1]);
        
        int leftChildx = o.child[0] != null ? o.child[0].getRect().x : o.child[1].getRect().x;
        int rightChildx = o.child[1] == null ? o.child[0].getRect().x : o.child[1].getRect().x;
        //根据左右两边孩子的节点，确定父节点的坐标尺寸
        int parentx = (leftChildx+rightChildx)/2;
        int parenty =o.getLevel()*levelHeight;
        o.setRect(new Rectangle(parentx, parenty, widthNode, heightNode));
    }
    
    private void prepareGraphic(){
        prepareNodeLevel(T, 0);
        prepareNodeSize(T);
    }
    
}

package com.hjzgg.rbt;

import java.util.Scanner;

public class RBTree {
    public RBTNode T = null;
    private boolean isRoot = true;//是不是第一个插入的节点，也就是根节点
    
    public void rotateT(RBTNode o, int rotate){//rotate表明旋转方向
        RBTNode k = o.child[rotate^1];
        if(o.parent==null)
            T = k;
        else if(o.parent.child[0] == o)
            o.parent.child[0] = k;
        else
            o.parent.child[1] = k;
        k.parent = o.parent;
        o.child[rotate^1] = k.child[rotate];
        k.child[rotate] = o;
        o.parent = k;
    }
    
    private void rbtInsertFixup(RBTNode o){//红黑树平衡的调整,并更改节点的颜色
        if(o.parent.color == RBTNode.RED){
            int childIndex;//左子树或者是右子树索引
            if(o.parent == o.parent.parent.child[0])
                childIndex = 0;
            else 
                childIndex = 1;
            
            //找到o节点对应的叔节点
            RBTNode ou = o.parent.parent.child[childIndex^1];
            if(ou!=null && ou.color == RBTNode.RED){//如果叔节点的颜色是红色
                o.parent.parent.color = RBTNode.RED;
                ou.color = RBTNode.BLACK;
                o.parent.color = RBTNode.BLACK;
            } else {//叔节点是空或者是黑色
                if(o == o.parent.child[childIndex^1]){
                    o = o.parent;
                    rotateT(o, childIndex);
                }
                o.parent.color = RBTNode.BLACK;
                o.parent.parent.color = RBTNode.RED;
                rotateT(o.parent.parent, childIndex^1);
            }
            T.color = RBTNode.BLACK;
        }
    }
    
    public void outT(RBTNode o){
        if(o==null) return;
        System.out.print(o.key+" ");
        outT(o.child[0]);
        outT(o.child[1]);
    }
    
    public void rbtInsert(RBTNode o, RBTNode op, int key, int childIndex){//红黑树的插入
        if(o == null){
            o = new RBTNode(op, key, RBTNode.RED);
            if(op==null){
                T = o;
                T.color = RBTNode.BLACK;
            } else {
                op.child[childIndex] = o;
                o.parent = op;
            }
            if(o.color==RBTNode.RED)
                rbtInsertFixup(o);
        } else if(o.key < key){
            rbtInsert(o.child[0], o, key, 0);
            if(o.color==RBTNode.RED)
                rbtInsertFixup(o);
        } else {
            rbtInsert(o.child[1], o, key, 1);
            if(o.color==RBTNode.RED)
                rbtInsertFixup(o);
        }
    }
    
    public void rbtDelete(){//红黑树的删除
        
    }
    

    public static void main(String[] args) {
        RBTree rbt = new RBTree();
        Scanner scan = new Scanner(System.in);
        for(int i=0; i<15; ++i){
            int key = scan.nextInt();
            rbt.rbtInsert(rbt.T, null, key, 0);
//            rbt.outT(rbt.T);
//            System.out.println();
        }
        new RBTGraphic(rbt.T).new TreeFrame("红黑树");
    }
}

/*
  2 3 4 6 7 9 11 9 18 14 12 17 19 22 20
  */