2021年四月CCF-CSP认证题目

灰度直方图

题目描述

一幅长宽分别为 n 个像素和 m 个像素的灰度图像可以表示为一个 n×m 大小的矩阵 A。其中每个元素 Aij（0≤i<n、0≤j<m）是一个 [0,L) 范围内的整数，表示对应位置像素的灰度值。具体来说，一个 8 比特的灰度图像中每个像素的灰度范围是 [0,128)。
一副灰度图像的灰度统计直方图（以下简称“直方图”）可以表示为一个长度为 L 的数组 h，其中 h[x]（0≤x<L）表示该图像中灰度值为 x 的像素个数。显然，h[0] 到 h[L−1] 的总和应等于图像中的像素总数 n⋅m。
已知一副图像的灰度矩阵 A，试计算其灰度直方图 h[0],h[1],⋯,h[L−1]。

输出格式

输出到标准输出。
输出仅一行，包含用空格分隔的 L 个整数 h[0],h[1],⋯,h[L−1]，表示输入图像的灰度直方图。
全部的测试数据满足 0<n,m≤500 且 4≤L≤256。

样例2输入

7 11 8
0 7 0 0 0 7 0 0 7 7 0
7 0 7 0 7 0 7 0 7 0 7
7 0 0 0 7 0 0 0 7 0 7
7 0 0 0 0 7 0 0 7 7 0
7 0 0 0 0 0 7 0 7 0 0
7 0 7 0 7 0 7 0 7 0 0
0 7 0 0 0 7 0 0 7 0 0

样例2输出

48 0 0 0 0 0 0 29

AC代码

#include <iostream>
const int N = 510;
const int M = 510;
const int a[N][M] = {0};

int main()
{
	int L,m,n,x;
	scanf("%d%d%d", &m, &n, &L);
	int h[L] = {0};
	for (int i = 0; i< m*n; i++)
	{
		scanf("%d", &x);
		h[x]++;
	}
	for (int i = 0; i< L; i++) printf("%d ", h[i]);
	return 0;
}

邻域均值

题目背景

顿顿在学习了数字图像处理后，想要对手上的一副灰度图像进行降噪处理。不过该图像仅在较暗区域有很多噪点，如果贸然对全图进行降噪，会在抹去噪点的同时也模糊了原有图像。因此顿顿打算先使用邻域均值来判断一个像素是否处于较暗区域，然后仅对处于较暗区域的像素进行降噪处理。

题目描述

待处理的灰度图像长宽皆为 n 个像素，可以表示为一个 n×n 大小的矩阵 A，其中每个元素是一个 [0,L) 范围内的整数，表示对应位置像素的灰度值。对于矩阵中任意一个元素 Aij（0≤i,j<n），其邻域定义为附近若干元素的集和：
Neighbor(i,j,r)={Axy|0≤x,y<n and |x−i|≤r and |y−j|≤r}
这里使用了一个额外的参数 r 来指明 Aij 附近元素的具体范围。根据定义，易知 Neighbor(i,j,r) 最多有 (2r+1)2 个元素。
如果元素 Aij 邻域中所有元素的平均值小于或等于一个给定的阈值 t，我们就认为该元素对应位置的像素处于较暗区域。下图给出了两个例子，左侧图像的较暗区域在右侧图像中展示为黑色，其余区域展示为白色。现给定邻域参数 r 和阈值 t，试统计输入灰度图像中有多少像素处于较暗区域。

输入格式

从标准输入读入数据。
输入共 n+1 行。
输入的第一行包含四个用空格分隔的正整数 n、L、r 和 t，含义如前文所述。
第二到第 n+1 行输入矩阵 A。第 i+2（0≤i<n）行包含用空格分隔的 n 个整数，依次为 Ai0,Ai1,⋯,Ai(n−1)。

输出格式

输出到标准输出。
输出一个整数，表示输入灰度图像中处于较暗区域的像素总数。
70% 的测试数据满足 n≤100、r≤10。
全部的测试数据满足 0<n≤600、0<r≤100 且 2≤t<L≤256。

样例1输入

4 16 1 6
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15

样例1输出

样例2输入

11 8 2 2
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 7 0 0 0 7 0 0 7 7 0
7 0 7 0 7 0 7 0 7 0 7
7 0 0 0 7 0 0 0 7 0 7
7 0 0 0 0 7 0 0 7 7 0
7 0 0 0 0 0 7 0 7 0 0
7 0 7 0 7 0 7 0 7 0 0
0 7 0 0 0 7 0 0 7 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0

样例2输出

未AC代码(有空继续做，tmd二维前缀和怎么不会做了)

#include <iostream>
using namespace std;
int main()
{
	int n,r,t,L,blacksum;
	scanf("%d%d%d%d", &n, &L, &r, &t);
	int pic[n][n] = {0};
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
			scanf("%d", &pic[i][j]);
	}
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			bool flag = 0;
			int sum = 0;
			int cnt = 0;
			for (int p=i-r; p<=i+r; p++)
			{
				if (p<0||p>=n) continue;
				for (int q=j-r; q<=j+r; q++)
				{
					if(q<0||q>=n) continue;
					cnt++;
					sum += pic[p][q];
				}
			}
			if (sum*1.0/cnt<=double(t)) flag = 1;
			if (flag) blacksum++;	
		}		
	}
	cout<<blacksum;
}

DHCP

题目背景

动态主机配置协议（Dynamic Host Configuration Protocol, DHCP）是一种自动为网络客户端分配 IP 地址的网络协议。当支持该协议的计算机刚刚接入网络时，它可以启动一个 DHCP 客户端程序。后者可以通过一定的网络报文交互，从 DHCP 服务器上获得 IP 地址等网络配置参数，从而能够在用户不干预的情况下，自动完成对计算机的网络设置，方便用户连接网络。DHCP 协议的工作过程如下：
当 DHCP 协议启动的时候，DHCP 客户端向网络中广播发送 Discover 报文，请求 IP 地址配置；
当 DHCP 服务器收到 Discover 报文时，DHCP 服务器根据报文中的参数选择一个尚未分配的 IP 地址，分配给该客户端。DHCP 服务器用 Offer 报文将这个信息传达给客户端；
客户端收集收到的 Offer 报文。由于网络中可能存在多于一个 DHCP 服务器，因此客户端可能收集到多个 Offer 报文。客户端从这些报文中选择一个，并向网络中广播 Request 报文，表示选择这个 DHCP 服务器发送的配置；
DHCP 服务器收到 Request 报文后，首先判断该客户端是否选择本服务器分配的地址：如果不是，则在本服务器上解除对那个 IP 地址的占用；否则则再次确认分配的地址有效，并向客户端发送 Ack 报文，表示确认配置有效，Ack 报文中包括配置的有效时间。如果 DHCP 发现分配的地址无效，则返回 Nak 报文；
客户端收到 Ack 报文后，确认服务器分配的地址有效，即确认服务器分配的地址未被其它客户端占用，则完成网络配置，同时记录配置的有效时间，出于简化的目的，我们不考虑被占用的情况。若客户端收到 Nak 报文，则从步骤 1 重新开始；
客户端在到达配置的有效时间前，再次向 DHCP 服务器发送 Request 报文，表示希望延长 IP 地址的有效期。DHCP 服务器按照步骤 4 确定是否延长，客户端按照步骤 5 处理后续的配置；
在本题目中，你需要理解 DHCP 协议的工作过程，并按照题目的要求实现一个简单的 DHCP 服务器。

题目描述

报文格式

为了便于实现，我们简化地规定 DHCP 数据报文的格式如下：
<发送主机> <接收主机> <报文类型> <IP 地址> <过期时刻>
DHCP 数据报文的各个部分由空格分隔，其各个部分的定义如下：
发送主机：是发送报文的主机名，主机名是由小写字母、数字组成的字符串，唯一地表示了一个主机；
接收主机：当有特定的接收主机时，是接收报文的主机名；当没有特定的接收主机时，为一个星号（*）；
报文类型：是三个大写字母，取值如下：
DIS：表示 Discover 报文；
OFR：表示 Offer 报文；
REQ：表示 Request 报文；
ACK：表示 Ack 报文；
NAK：表示 Nak 报文；
IP 地址，是一个非负整数：
对于 Discover 报文，该部分在发送的时候为 0，在接收的时候忽略；
对于其它报文，为正整数，表示一个 IP 地址；
过期时刻，是一个非负整数：
对于 Offer、Ack 报文，是一个正整数，表示服务器授予客户端的 IP 地址的过期时刻；
对于 Discover、Request 报文，若为正整数，表示客户端期望服务器授予的过期时刻；
对于其它报文，该部分在发送的时候为 0，在接收的时候忽略。
例如下列都是合法的 DHCP 数据报文：

a * DIS 0 0
d a ACK 50 1000

服务器配置

为了 DHCP 服务器能够正确分配 IP 地址，DHCP 需要接受如下配置：

地址池大小 N：表示能够分配给客户端的 IP 地址的数目，且能分配的 IP 地址是 1,2,…,N；
默认过期时间 Tdef：表示分配给客户端的 IP 地址的默认的过期时间长度；
过期时间的上限和下限 Tmax、Tmin：表示分配给客户端的 IP 地址的最长过期时间长度和最短过期时间长度，客户端不能请求比这个更长或更短的过期时间；
本机名称 H：表示运行 DHCP 服务器的主机名。

分配策略

当客户端请求 IP 地址时，首先检查此前是否给该客户端分配过 IP 地址，且该 IP 地址在此后没有被分配给其它客户端。如果是这样的情况，则直接将 IP 地址分配给它，否则，总是分配给它最小的尚未占用过的那个 IP 地址。如果这样的地址不存在，则分配给它最小的此时未被占用的那个 IP 地址。如果这样的地址也不存在，说明地址池已经分配完毕，因此拒绝分配地址。

实现细节

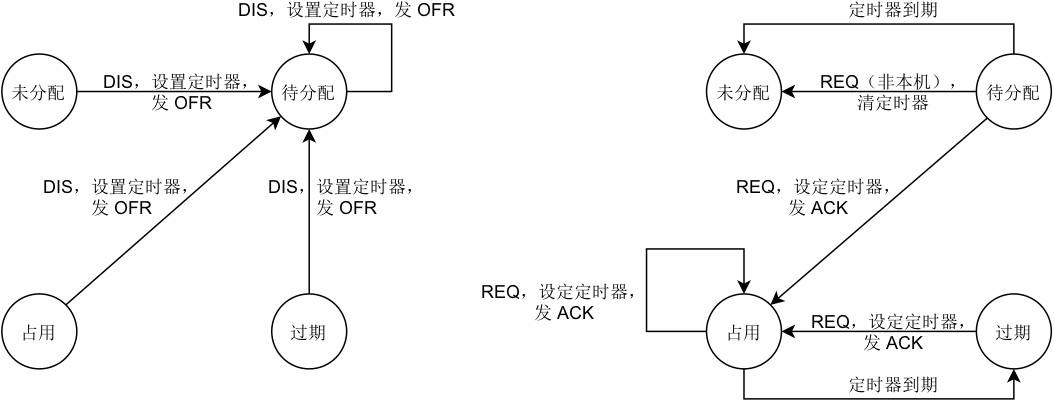
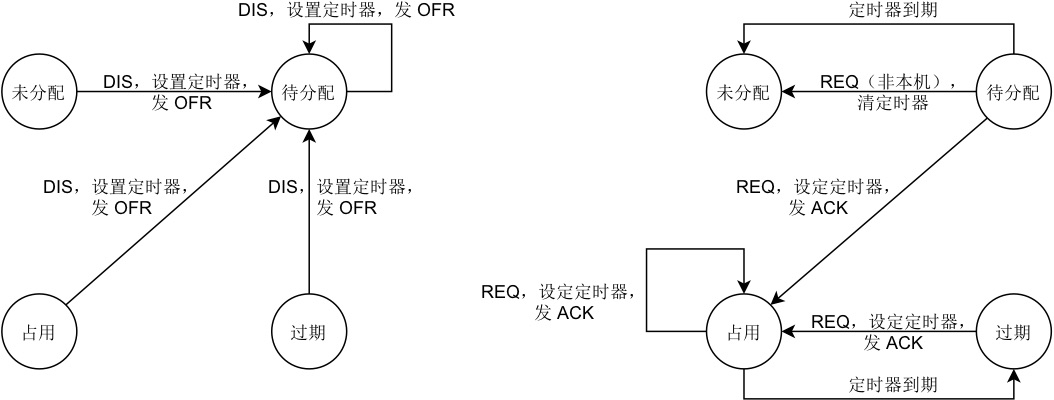
在 DHCP 启动时，首先初始化 IP 地址池，将所有地址设置状态为未分配，占用者为空，并清零过期时刻。其中地址的状态有未分配、待分配、占用、过期四种。处于未分配状态的 IP 地址没有占用者，而其余三种状态的 IP 地址均有一名占用者。处于待分配和占用状态的 IP 地址拥有一个大于零的过期时刻。在到达该过期时刻时，若该地址的状态是待分配，则该地址的状态会自动变为未分配，且占用者清空，过期时刻清零；否则该地址的状态会由占用自动变为过期，且过期时刻清零。处于未分配和过期状态的 IP 地址过期时刻为零，即没有过期时刻。

对于收到的报文，设其收到的时刻为 t。处理细节如下：

判断接收主机是否为本机，或者为 *，若不是，则判断类型是否为 Request，若不是，则不处理；
若类型不是 Discover、Request 之一，则不处理；
若接收主机为 *，但类型不是 Discover，或接收主机是本机，但类型是 Discover，则不处理。
对于 Discover 报文，按照下述方法处理：

检查是否有占用者为发送主机的 IP 地址：
若有，则选取该 IP 地址；
若没有，则选取最小的状态为未分配的 IP 地址；
若没有，则选取最小的状态为过期的 IP 地址；
若没有，则不处理该报文，处理结束；
将该 IP 地址状态设置为待分配，占用者设置为发送主机；
若报文中过期时刻为 0 ，则设置过期时刻为 t+Tdef；否则根据报文中的过期时刻和收到报文的时刻计算过期时间，判断是否超过上下限：若没有超过，则设置过期时刻为报文中的过期时刻；否则则根据超限情况设置为允许的最早或最晚的过期时刻；
向发送主机发送 Offer 报文，其中，IP 地址为选定的 IP 地址，过期时刻为所设定的过期时刻。
对于 Request 报文，按照下述方法处理：

检查接收主机是否为本机：
若不是，则找到占用者为发送主机的所有 IP 地址，对于其中状态为待分配的，将其状态设置为未分配，并清空其占用者，清零其过期时刻，处理结束；
检查报文中的 IP 地址是否在地址池内，且其占用者为发送主机，若不是，则向发送主机发送 Nak 报文，处理结束；
无论该 IP 地址的状态为何，将该 IP 地址的状态设置为占用；
与 Discover 报文相同的方法，设置 IP 地址的过期时刻；
向发送主机发送 Ack 报文。
上述处理过程中，地址池中地址的状态的变化可以概括为如下图所示的状态转移图。为了简洁，该图中没有涵盖需要回复 Nak 报文的情况。

输入格式

从标准输入读入数据。
输入的第一行包含用空格分隔的四个正整数和一个字符串，分别是：N、Tdef、Tmax、Tmin 和 H，保证 Tmin≤Tdef≤Tmax。
输入的第二行是一个正整数 n，表示收到了 n 个报文。
输入接下来有 n 行，第 (i+2) 行有空格分隔的正整数 ti 和约定格式的报文 Pi。表示收到的第 i 个报文是在 ti 时刻收到的，报文内容是 Pi。保证 ti<ti+1。

输出格式

输出到标准输出。
输出有若干行，每行是一个约定格式的报文。依次输出 DHCP 服务器发送的报文。

样例1输入

4 5 10 5 dhcp
16
1 a * DIS 0 0
2 a dhcp REQ 1 0
3 b a DIS 0 0
4 b * DIS 3 0
5 b * REQ 2 12
6 b dhcp REQ 2 12
7 c * DIS 0 11
8 c dhcp REQ 3 11
9 d * DIS 0 0
10 d dhcp REQ 4 20
11 a dhcp REQ 1 20
12 c dhcp REQ 3 20
13 e * DIS 0 0
14 e dhcp REQ 2 0
15 b dhcp REQ 2 25
16 b * DIS 0 0

样例1输出

dhcp a OFR 1 6
dhcp a ACK 1 7
dhcp b OFR 2 9
dhcp b ACK 2 12
dhcp c OFR 3 12
dhcp c ACK 3 13
dhcp d OFR 4 14
dhcp d ACK 4 20
dhcp a ACK 1 20
dhcp c ACK 3 20
dhcp e OFR 2 18
dhcp e ACK 2 19
dhcp b NAK 2 0

样例1解释

输入第一行，分别设置了 DHCP 的相关参数，并收到了 16 个报文。

第 1 个报文和第 2 个报文是客户端 a 正常请求地址，服务器为其分配了地址 1，相应地设置了过期时刻是 7（即当前时刻 2 加上默认过期时间 5）。

第 3 个报文不符合 Discover 报文的要求，不做任何处理。

第 4 个报文 b 发送的 Discover 报文虽然有 IP 地址 3，但是按照处理规则，这个字段被忽略，因此服务器返回 Offer 报文，过期时刻是 9。

第 5 个报文中，Request 报文不符合接收主机是 DHCP 服务器本机的要求，因此不做任何处理。

第 6 个报文是 b 发送的 Request 报文，其中设置了过期时刻是 12，没有超过最长过期时间，因此返回的 Ack 报文中过期时刻也是 12。

第 7 个报文中，过期时刻 11 小于最短过期时间，因此返回的过期时刻是 12。虽然此时为 a 分配的地址 1 过期，但是由于还有状态为未分配的地址 3，因此为 c 分配地址 3。第 8 个报文同理，为 c 分配的地址过期时刻是 13。

第 9、10 两个报文中，为 d 分配了地址 4，过期时刻是 20。

第 11 个报文中，a 请求重新获取此前为其分配的地址 1，虽然为其分配的地址过期，但是由于尚未分配给其它客户端，因此 DHCP 服务器可以直接为其重新分配该地址，并重新设置过期时刻为 20。

第 12 个报文中，c 请求延长其地址的过期时刻为 20。DHCP 正常向其回复 Ack 报文。

第 13、14 个报文中，e 试图请求地址。此时地址池中已经没有处于“未分配”状态的地址了，但是有此前分配给 b 的地址 2 的状态是“过期”，因此把该地址重新分配给 e。

第 15 个报文中，b 试图重新获取此前为其分配的地址 2，但是此时该地址已经被分配给 e，因此返回 Nak 报文。

第 16 个报文中，b 试图重新请求分配一个 IP 地址，但是此时地址池中已经没有可用的地址了，因此忽略该请求。

样例2输入

4 70 100 50 dhcp
6
5 a * OFR 2 100
10 b * DIS 0 70
15 b dhcp2 REQ 4 60
20 c * DIS 0 70
70 d * DIS 0 120
75 d dhcp REQ 1 125

样例2输出

dhcp b OFR 1 70
dhcp c OFR 1 70
dhcp d OFR 1 120
dhcp d ACK 1 125

样例2解释

在本样例中，DHCP 服务器一共收到了 6 个报文，处理情况如下：

第 1 个报文不是 DHCP 服务器需要处理的报文，因此不回复任何报文。

第 2 个报文中，b 请求分配 IP 地址，因此 DHCP 服务器将地址 1 分配给 b，此时，地址 1 进入待分配状态，DHCP 服务器向 b 发送 Offer 报文。

第 3 个报文中，b 发送的 REQ 报文是发给非本服务器的，因此需要将地址池中所有拥有者是 b 的待分配状态的地址修改为未分配。

第 4 个报文中，c 请求分配 IP 地址。由于地址 1 此时是未分配状态，因此将该地址分配给它，向它发送 Offer 报文，地址 1 进入待分配状态。

第 5、6 个报文中，d 请求分配 IP 地址。注意到在收到第 5 个报文时，已经是时刻 70，地址 1 的过期时刻已到，它的状态已经被修改为了未分配，因此 DHCP 服务器仍然将地址 1 分配给 d。

子任务

对于 20% 的数据，有 N≤200，且 n≤N，且输入仅含 Discover 报文，且 t<Tmin；
对于 50% 的数据，有 N≤200，且 n≤N，且 t<Tmin，且报文的接收主机或为本机，或为 *；
对于 70% 的数据，有 N≤1000，且 n≤N，且报文的接收主机或为本机，或为 *；
对于 100% 的数据，有 N≤10000，且 n≤10000，主机名的长度不超过 20，且 t,Tmin,Tdefault,Tmax≤109，输入的报文格式符合题目要求，且数字不超过 109。

校门外的树

X 校最近打算美化一下校园环境。前段时间因为修地铁，X 校大门外种的行道树全部都被移走了。现在 X 校打算重新再种一些树，为校园增添一抹绿意。

X 校大门外的道路是东西走向的，我们可以将其看成一条数轴。在这条数轴上有 n 个障碍物，例如电线杆之类的。虽然障碍物会影响树的生长，但是障碍物不一定能被随便移走，所以 X 校规定在障碍物的位置上不能种树。n 个障碍物的坐标都是整数；如果规定向东为正方向，则 n 个障碍物的坐标按照从西到东的顺序分别为 a1,a2,⋯,an。X 校打算在 [a1,an] 之间种一些树，使得这些树看起来比较美观。

X 校希望，在一定范围内，树应该是等间隔的。更具体地说，如果把 [a1,an) 划分成一些区间 [ap1,ap2),⋯,[apm−1,apm)（1=p1<p2<⋯<pm=n），那么每个区间 [api,api+1) 内需要至少种一棵树，且该区间内种的树的坐标连同区间端点 api,api+1 应该构成一个等差数列。不同区间的公差，也就是树的间隔可以不相同。

例如，如果障碍物位于 0,2,6 这三处，那么我们可以选择在 [0,2) 和 [2,6) 分别种树，也可以选择在 [0,6) 等间隔种树。如果是分别在 [0,2) 和 [2,6) 种树，由于每个区间内至少要种一棵树，坐标 1 上必须种树；而 [2,6) 上的树可以按照 1 的间隔种下，也可以按照 2 的间隔种下。下图表示了这两种美观的种树方案，其中橙色的圆表示障碍物，绿色的圆表示需要在这个位置种树，箭头上的数字表示种下这棵树时对应的间隔为多少。

对区间 [0,2) 和 [2,6) 分别以 1 和 2 的间隔种树是美观的

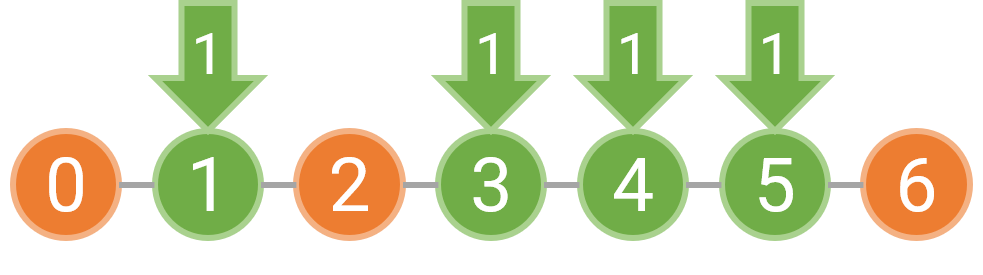
对区间 [0, 2) 和 [2, 6) 分别以 1 的间隔种树也是美观的
而如果选择在 [0,6) 区间等间隔种树，我们只能以 3 的间隔种树，因为无论是选择间隔 1 或者间隔 2，都需要在坐标 2 上种树，而这个位置已经有障碍物了。下图分别表示了间隔为 3,2,1 时的种树情况，红色箭头表示不能在这里种树。

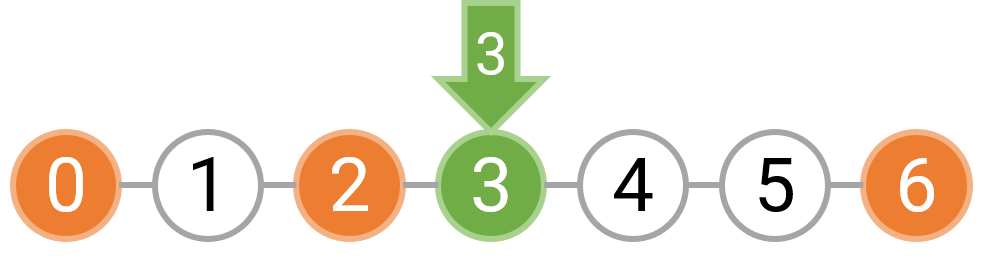
对区间 [0, 6) 以 3 的间隔种树是美观的

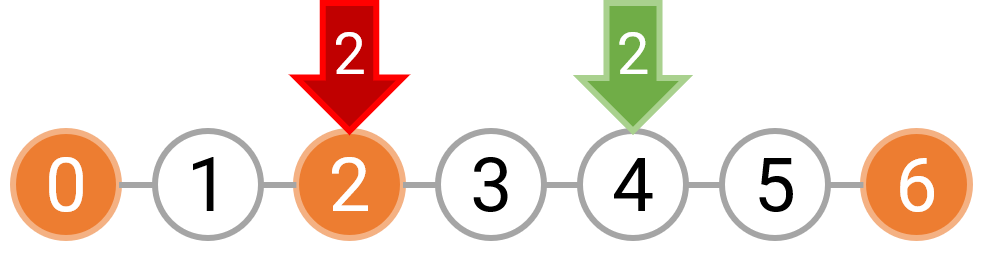
图 4: 对区间 [0, 6) 以 2 的间隔种树是不美观的

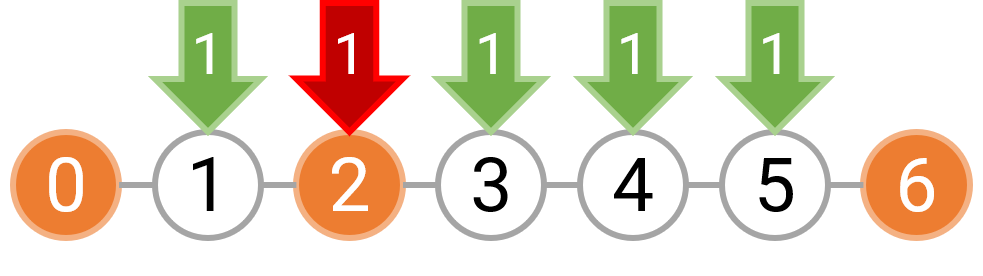
图 5: 对区间 [0, 6) 以 1 的间隔种树也是不美观的
一般地，给定一个区间 [al,ar)，对于树的坐标的集合 T⊂(al,ar)（T⊂Z），归纳定义 T 在 [al,ar) 上是美观的：
如果 T≠∅，T∩{al,al+1,⋯,ar}=∅，并且存在一个公差 d≥1，使得 T∪{al,ar} 中的元素按照从小到大的顺序排序后，可以构成一个公差为 d 的等差数列（显然，这个等差数列的首项为 al，末项为 ar），则 T 在 [al,ar) 上是美观的；
如果 T∩{al,al+1,⋯,ar}=∅，并且存在一个下标 m（l<m<r），使得 T∩(al,am) 在 [al,am) 上是美观的，且 T∩(am,ar) 在 [am,ar) 上是美观的，则 T 在 [al,ar) 上是美观的。
根据这一定义，空集在任意区间上都不是美观的；另外，如果存在下标 i 使得 ai∈T，那么 T 一定不是美观的。
我们称两种种树的方案是本质不同的，当且仅当两种方案中，种树的坐标集合不同。请帮助 X 校对 [a1,an) 求出所有本质不同的美观的种树方案。当然，由于方案可能很多，你只需要输出总方案数对 10^9+7 取模的结果。

输出格式

输出到标准输出。
输出一个非负整数，表示本质不同的美观的种树方案的数量对 109+7 取模的结果。

样例1输入

3
0 2 6

样例1输出

样例1解释

这组样例即为题面描述中提到的那组。

样例2输入

11
0 10 20 30 40 50 60 70 80 90 100

样例2输出

256507

子任务

对于 10 的数据，保证 n=2；
对于 30 的数据，保证 n≤10；
对于 60 的数据，保证 n≤100,ai≤1000；
对于 100 的数据，保证 2≤n≤1000,0≤ai≤100,000，且至少存在一种美观的种树方案。

疫苗运输

题目描述

X 市最近生产了一批疫苗，需要运往各地使用。疫苗的运输是一个困难的问题：既要实现尽快时间送达，又要保证全程冷链，否则疫苗会损坏。

X 市的物流系统并不发达，只有 n 个物流站点（以下简称“站点”）和 m 条物流线路（以下简称“线路”），且该物流系统具有以下几个特点：

每条线路都是环线。即，从某个站点出发，经过一系列不重复的站点，最终回到出发站点。
每条线路上有且仅有一辆运输车，以固定的时刻表（相邻站间的时间间隔）在环线上不断运行。在 0 时刻时，运输车在出发站点。
运输车上配备了容量足够大的制冷系统，疫苗可以在车上长时间存放。但是换乘（从一条线路切换到另一条线路）必须在同一个站点同一个时刻发生——因为各个站点没有独立的制冷系统，疫苗不能在站点内下车等待。
现在 X 市想要从 1 号站点开始，经过若干条线路的运输和换乘，将疫苗运输到各个其他站点。与其他站点不同，1 号站点配有冷库。也就是说，从 0 时刻开始，可以在 1 号站点等待某条线路运输车的到来，再开始疫苗运输。问对于 2 号 ~ n 号站点，分别最早可以在什么时刻将疫苗送到该站点。

注意：每个问题是独立的，即只需要求出 1 号站点到各个站点的最早送达时刻。

输入格式

从标准输入读入数据。

第一行两个整数 n, m。

接下来 m 行，每行表示一条物流线路。对于第 i (1≤i≤m) 条线路，首先有一个整数 li (2≤li≤n) 表示该线路经过的站点个数。接下来 2li 个整数，第 2j−1 和第 2j 个整数分别表示该线路的第 j (1≤j≤li) 个站点的编号 ai,j (1≤ai,j≤n)，以及该线路的第 j 个站点到下一个站点所需的时间 ti,j (1≤ti,j≤T)（对于第 li 个站点即为它到第 1 个站点的时间）。其中，每条线路的第 1 个站点为其出发站点。输入中同一行相邻的整数，均用一个空格隔开。

输出格式

输出 n−1 行，第 i 行表示将疫苗送达第 i+1 个站点的最早时间：如果能在有限时间内送达，输出最早的送达时刻；否则输出 inf。

样例1输入

5 2
3 1 100 2 100 3 100
3 3 100 4 100 5 100

样例1输出

100
200
inf
inf

样例2输入

5 3
3 1 100 2 100 3 100
3 3 100 4 100 5 100
2 3 125 5 125

样例2输出

样例2解释

在此样例中，有 5 个站点、3 条线路。第一条线路经过站点 1、2、3，第二条线路经过站点 3、4、5，第三条线路经过站点 3 和 5。

以下为从 1 号站点到各个其他站点的最早送达路线：

2 号站点：通过第一条线路运输，在 100 时刻到达 2 号站点
3 号站点：通过第一条线路运输，在 200 时刻到达 3 号站点
4 号站点：通过第一条线路运输，在 500 时刻到达 3 号站点，然后换乘第三条线路，在 1500 时刻再次到达 3 号站点，最后换乘第二条线路，在 1600 时刻到达 4 号站点
5 号站点：通过第一条线路运输，在 500 时刻到达 3 号站点，然后换乘第三条线路，在 625 时刻到达 5 号站点

样例3输入

10 5
6 8 18 1 8 3 52 4 3 7 18 2 47
6 8 96 2 45 10 44 6 95 4 97 3 96
4 10 63 8 97 7 75 1 12
7 3 7 5 75 1 19 2 37 4 25 10 43 9 32
2 6 35 5 74

样例3输出

子任务

对于 10% 的数据，n≤5,m=1,T≤10。
对于 30% 的数据，n≤5,m≤2,T≤10。
对于 50% 的数据，n≤5,m≤5,T≤10。
对于 70% 的数据，n≤10,m≤10,T≤100。
对于 80% 的数据，n≤30,m≤30,T≤1000。
对于 95% 的数据，n≤100,m≤100,T≤10^5。
对于 100% 的数据，n≤500,m≤500,T≤10^6。

posted @ 2021-04-12 13:37 胡椒椒椒（弃用勿联系）阅读(1623) 评论(2) 编辑收藏举报

刷新页面返回顶部

胡椒椒椒

2021年四月CCF-CSP认证题目

灰度直方图

题目描述

输出格式

样例2输入

样例2输出

AC代码

邻域均值

题目背景

题目描述

输入格式

输出格式

样例1输入

样例1输出

样例2输入

样例2输出

未AC代码(有空继续做，tmd二维前缀和怎么不会做了)

DHCP

题目背景

题目描述

报文格式

服务器配置

分配策略

实现细节

输入格式

输出格式

样例1输入

样例1输出

样例1解释

样例2输入

样例2输出

样例2解释

子任务

校门外的树

输出格式

样例1输入

样例1输出

样例1解释

样例2输入

样例2输出

子任务

疫苗运输

题目描述

输入格式

输出格式

样例1输入

样例1输出

样例2输入

样例2输出

样例2解释

样例3输入

样例3输出

子任务

公告