我真的弄清楚KMP算法了，如果我还不懂我也没辙了( ｰ̀֊ｰ́ )✧

KMP 学习之路真的艰难，但总算站在前人的肩膀上能够 "板书"该算法了。惭愧惭愧
参考视频：
https://www.bilibili.com/video/BV1Px411z7Yo?from=search&seid=1580852786652056405&spm_id_from=333.337.0.0
https://www.bilibili.com/video/BV1hW411a7ys/?spm_id_from=333.788.recommend_more_video.0 灯老师的
本博客转载：https://blog.csdn.net/yearn520/article/details/6729426
知乎详解：https://www.zhihu.com/question/21923021/answer/1032665486

我们在一个母字符串中查找一个子字符串有很多方法。KMP是一种最常见的改进算法，它可以在匹配过程中失配的情况下，有效地多往后面跳几个字符，加快匹配速度。

当然我们可以看到这个算法针对的是子串有对称属性，如果有对称属性，那么就需要向前查找是否有可以再次匹配的内容。

 

在KMP算法中有个数组，叫做前缀数组，也有的叫next数组，每一个子串有一个固定的next数组，它记录着字符串匹配过程中失配情况下可以向前多跳几个字符，当然它描述的也是子串的对称程度，程度越高，值越大，当然之前可能出现再匹配的机会就更大。

这个next数组的求法是KMP算法的关键，但不是很好理解，我在这里用通俗的话解释一下，看到别的地方到处是数学公式推导，看得都蛋疼，这个篇文章仅贡献给不喜欢看数学公式又想理解KMP算法的同学。

 

1、用一个例子来解释，下面是一个子串的next数组的值，可以看到这个子串的对称程度很高，所以next值都比较大。

位置i	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
前缀next[i]	0	0	0	0	1	2	3	1	2	3	4	5	6	7	4	0
子串	a	g	c	t	a	g	c	a	g	c	t	a	g	c	t	g

申明一下：下面说的对称不是中心对称，而是中心字符块对称，比如不是abccba，而是abcabc这种对称。

（1）逐个查找对称串。

这个很简单，我们只要循环遍历这个子串，分别看前1个字符，前2个字符，3个... i个 最后到15个。

第1个a无对称，所以对称程度0

前两个ag无对称，所以也是0

依次类推前面0-4都一样是0

前5个agcta，可以看到这个串有一个a相等，所以对称程度为1前6个agctag，看得到ag和ag对成，对称程度为2

这里要注意了，想是这样想，编程怎么实现呢？

只要按照下面的规则：

a、当前面字符的前一个字符的对称程度为0的时候，只要将当前字符与子串第一个字符进行比较。这个很好理解啊，前面都是0，说明都不对称了，如果多加了一个字符，要对称的话最多是当前的和第一个对称。比如agcta这个里面t的是0，那么后面的a的对称程度只需要看它是不是等于第一个字符a了。

 

b、按照这个推理，我们就可以总结一个规律，不仅前面是0呀，如果前面一个字符的next值是1，那么我们就把当前字符与子串第二个字符进行比较，因为前面的是1，说明前面的字符已经和第一个相等了，如果这个又与第二个相等了，说明对称程度就是2了。有两个字符对称了。比如上面agctag，倒数第二个a的next是1，说明它和第一个a对称了，接着我们就把最后一个g与第二个g比较，又相等，自然对称成都就累加了，就是2了。

 

c、按照上面的推理，如果一直相等，就一直累加，可以一直推啊，推到这里应该一点难度都没有吧，如果你觉得有难度说明我写的太失败了。

当然不可能会那么顺利让我们一直对称下去，如果遇到下一个不相等了，那么说明不能继承前面的对称性了，这种情况只能说明没有那么多对称了，但是不能说明一点对称性都没有，所以遇到这种情况就要重新来考虑，这个也是难点所在。

 

（2）回头来找对称性

这里已经不能继承前面了，但是还是找对称成都嘛，最愚蠢的做法大不了写一个子函数，查找这个字符串的最大对称程度，怎么写方法很多吧，比如查找出所有的当前字符串，然后向前走，看是否一直相等，最后走到子串开头，当然这个是最蠢的，我们一般看到的KMP都是优化过的，因为这个串是有规律的。

在这里依然用上面表中一段来举个例子：   

位置i=0到14如下,我加的括号只是用来说明问题：

(a g c t a g c )( a g c t a g c) t

我们可以看到这段，最后这个t之前的对称程度分别是：1，2，3，4，5，6，7,倒数第二个c往前看有7个字符对称，所以对称为7。但是到最后这个t就没有继承前面的对称程度next值，所以这个t的对称性就要重新来求。

这里首要要申明几个事实

1、t 如果要存在对称性，那么对称程度肯定比前面这个c 的对称程度小，所以要找个更小的对称，这个不用解释了吧，如果大那么t就继承前面的对称性了。

2、要找更小的对称，必然在对称内部还存在子对称，而且这个t必须紧接着在子对称之后。

如下图说明。

 

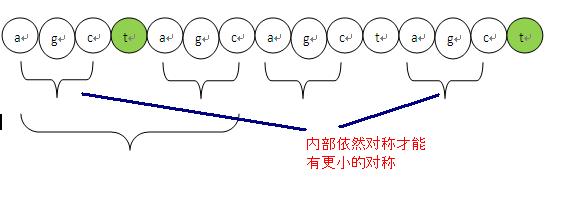
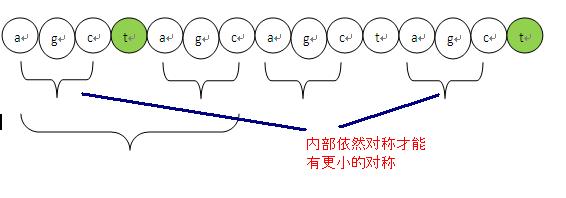
当时我唯一还存在的疑问就是为什么k next[k-1]=

这是我们的模式串： A B A B C A B A 当我们添加A进去发生不匹配。 可以认为是用前缀（ABAB）去匹配后缀(ABAA)。当最后一个字母：B和A不匹配时，用前缀的子串（ABA）的最长公共前后缀再去匹配后缀（ABAA）。而n-1对应的prefix表：prefix【n-1】就存储着子串（ABA）的最长公共前后缀的长度，所以k = next[k - 1], 这也就是“斜着”匹配的原因到了答案 下面我们从知乎上找这里： https://www.zhihu.com/question/21923021/answer/1032665486 从上面的理论我们就能得到下面的前缀next数组的求解算法。

void SetPrefix(const char *Pattern, int prefix[])

{

     int len=CharLen(Pattern);//模式字符串长度。

     prefix[0]=0;

     for(int i=1; i<len; i++)

     {

         int k=prefix[i-1];

         //不断递归判断是否存在子对称，k=0说明不再有子对称，Pattern[i] != Pattern[k]说明虽然对称，但是对称后面的值和当前的字符值不相等，所以继续递推

         while( Pattern[i] != Pattern[k]  &&  k!=0 )               

             k=prefix[k-1];     //继续递归

         if( Pattern[i] == Pattern[k])//找到了这个子对称，或者是直接继承了前面的对称性，这两种都在前面的基础上++

              prefix[i]=k+1;

         else

              prefix[i]=0;       //如果遍历了所有子对称都无效，说明这个新字符不具有对称性，清0

     }

}

通过这个说明，估计能够理解KMP的next求法原理了，剩下的就很简单了。我自己也有点晕了，实在不喜欢那些数学公式，所以用形象逻辑思维方法总结了一下。

 

然后呢总的Java 代码为：

package TenkindsOfAlgorithm.patternMatch;

import java.util.ArrayList;
import java.util.List;

public class kmp {
public static void main(String[] args) {
String p = "ABABCABAB";
int[] next = new int[p.length()];
getPrefixTable(p,next);
getNext(next);
for (int i = 0; i < next.length; i++) {
System.out.println(next[i]);
}
System.out.println(kmpSearch("ABABABABCABABABABCABAB", p, next));
}

/**
 * kmp
 */

public static List<Integer> kmpSearch(String s1, String p1, int []next){
    ArrayList<Integer> list = new ArrayList<>();
    char[] s = s1.toCharArray();
    char[] p = p1.toCharArray();
    int i =0;
    int j = 0;
    while (i<s.length && j<p.length){
        if (s[i]==p[j]){
            i++;
            j++;
        }else {
            // 灵魂
            j = next[j];
        }
        // 这里是处理多匹配问题 使用集合装入下标
        if (j== p.length-1 && s[i]==p[j]){ // 找到了 匹配完毕
            list.add(i-j+1);
            i++;
            j = next[j];
            j++;
        }
    }
    return list;
}
/**
 * len 表示含自身最长公共前后缀长度
 */
public static void getPrefixTable(String p, int[] next) {
    char[] pattern = p.toCharArray();
    next[0] = 0;
    for (int i = 1; i < pattern.length; i++) {
        int k = next[i-1];
        // 不断递归寻找子对称 , k=0之后说明不会再有子对称
        while (pattern[i]!=pattern[k] && k>0){
            k = next[k-1];
        }
        if (pattern[i]==pattern[k]){
            next[i] = k+1;
        }else {
            next[i] = 0;
        }
    }
}
public static void getNext(int []preTable){
    for (int i = preTable.length-1; i >0 ; i--) {
        preTable[i] = preTable[i-1];
    }
    preTable[0] = -1;
}

}