2021/10/1+10/2 图Graph的创建 + dfs + bfs

2021/10/1 图Graph

为什么要有图：

当我们需要表示多对多的关系时。

图是一种数据结构，其中结点可以具有零个或多个相邻元素。二个结点之间的连接为边

术语介绍

1）顶点（vertex）又叫结点

2）边（edge）

3）路径

4）无向图、有向图

5)顶点的度：是指依附于某顶点v的边数，通常记为TD(v)

使用集合表示图：

1. 无向图：E =
2. 有向图：G =

1、图的表示方式

1、邻接矩阵

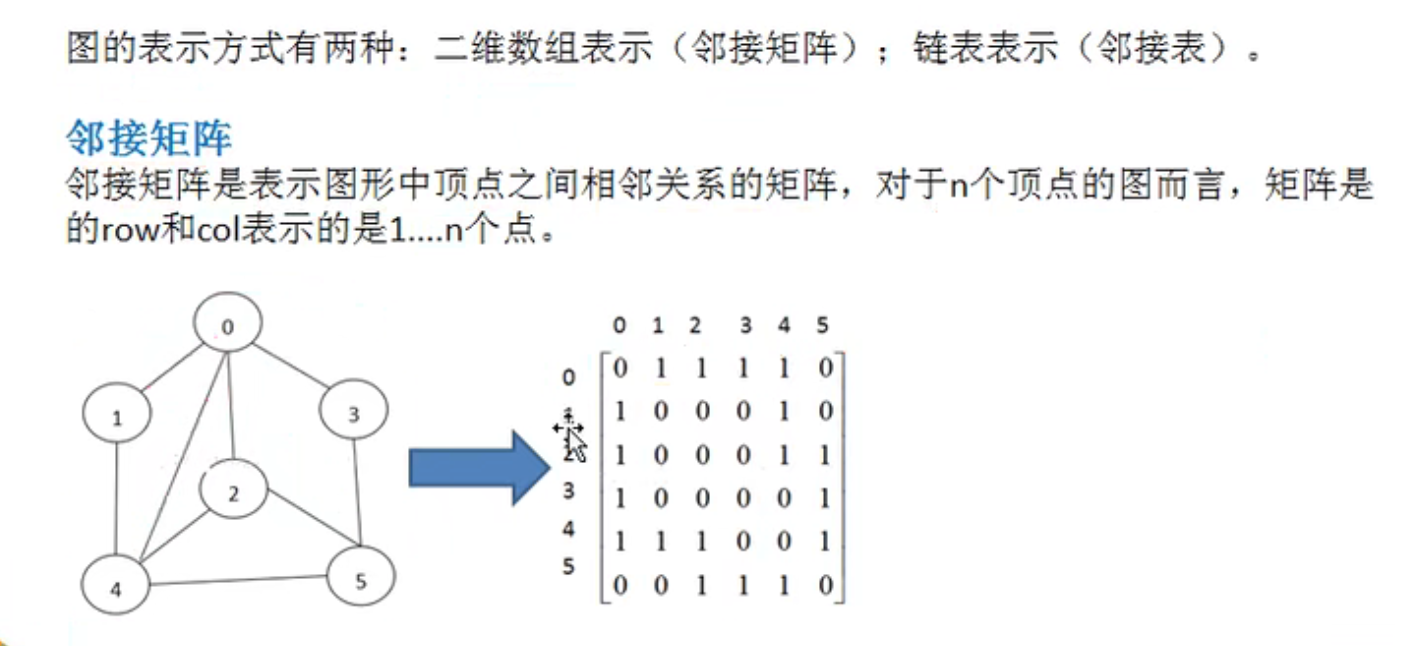
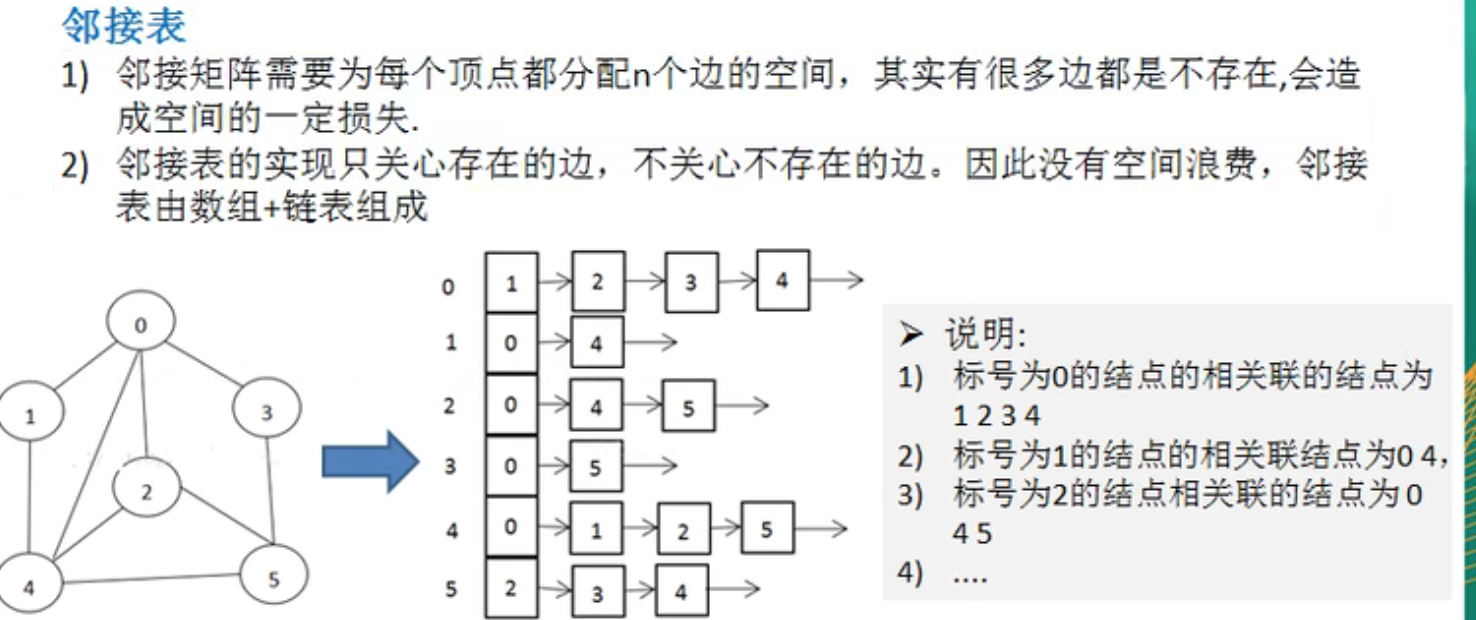
2、邻接表

2、图的代码实现

思路:1、使用List保存顶点信息

​ 2、使用二维数组保存节点于节点之间的信息

3、图的遍历

dfs:depth first search 深度优先搜索

• 类似树的先根遍历

bfs：breadth first search 广度优先算法

• 类似树的按参差遍历

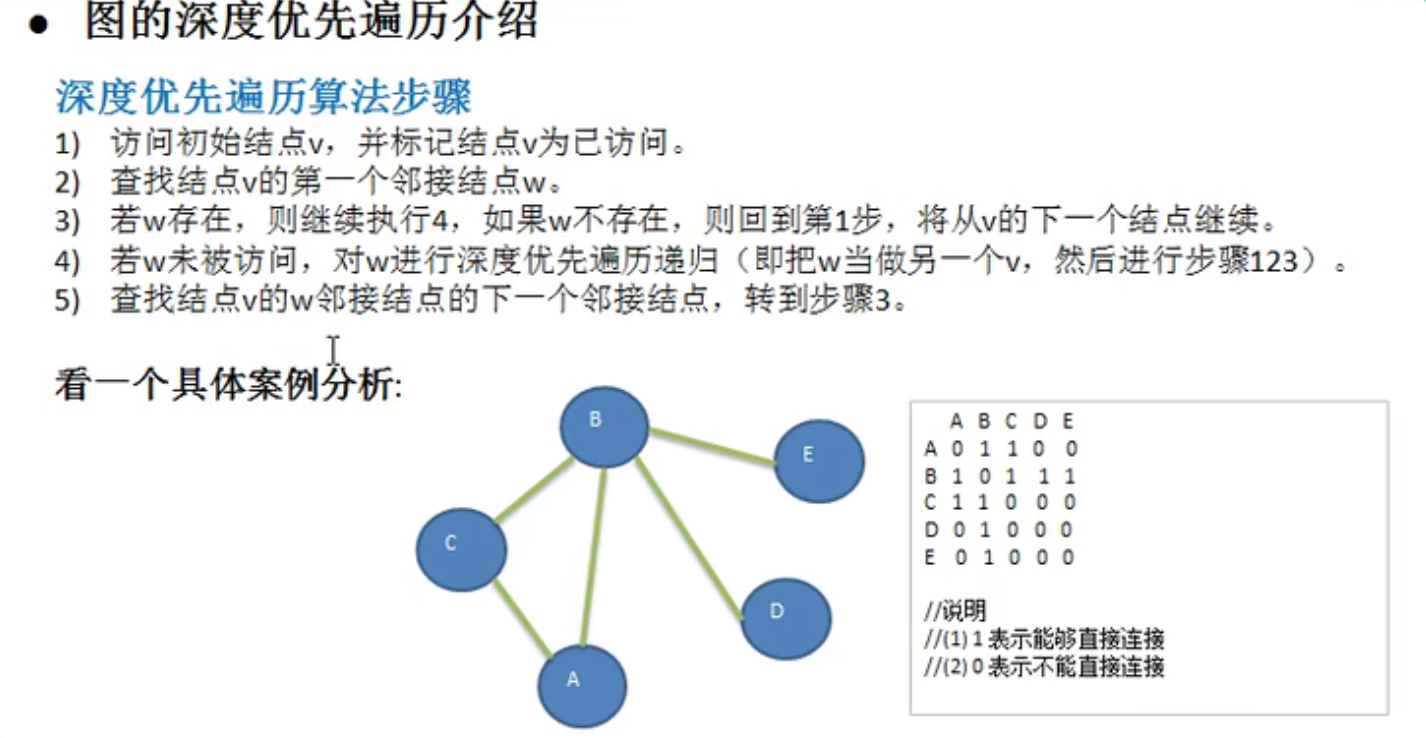
[0, 1, 1, 0, 0]
[1, 0, 1, 1, 1]
[1, 1, 0, 0, 0]
[0, 1, 0, 0, 0]
[0, 1, 0, 0, 0]

具体代码和八皇后很类似：

所以我们在思考使用DFS进行解决问题的时候需要思考这两个问题：是否有条件不成立的信息（w=-1），是否有条件成立的信息（for循环结束）

getFirstNeighbor 结合矩阵 指获得第一个相邻节点。

getNextNeighbor 指获得下一个相邻节点

public void dfs(int i){
  System.out.println(getNodeNameByIndex(i));
  isVisited[i]= true;
  /**
         * 很重要的代码  w!=-1 表明没有与他相连的结点了
         *             for循环的结束表明遍历完了
         */
  for (int w = getFirstNeighbor(i); w!=-1 ; w=getNextNeighbor(i,w)) {
    if (!isVisited[w]){
      dfs(w);
    }
  }
}
public int getFirstNeighbor(int index){
  for (int i = 0; i < vertexList.size(); i++) {
    if(edges.get(index).get(i)==1){
      return i;
    }
  }
  return -1;
}
public int getNextNeighbor(int i,int j){
  for (int k = j+1; k < vertexList.size(); k++) {
    if (edges.get(i).get(k)==1){
      return k;
    }
  }
  return -1;
}

2021/10/2 bfs

1、广度优先遍历基本思想：

图的广度优先搜索（Broad First Search）

2、代码实现：

public void bfsV2(int i){
        int u ;// 表示队列头节点对应的下标
        int w; // 表示邻结点下标
        System.out.println(getNodeNameByIndex(i));
        deque.add(i);
        isAdded[i] = true;
        while(!deque.isEmpty()){
            // 取出队列头
            u = (int) deque.pop();// 获取邻结点
            for ( w= getFirstNeighbor(u); w !=-1 ; w=getNextNeighbor(u,w)) {
                // 未被加入队列
                if(isAdded[w]==false){
                    System.out.println(getNodeNameByIndex(w));
                    isAdded[w] = true;
                    deque.add(w);
                }
            }
        }
    }
    /**
     * 可能会有非连通结点的情况 所以我们需要遍历
     */
    public void bfsV2(){
        for (int i = 0; i < vertexList.size(); i++) {
            if(isAdded[i]==false){
                bfsV2(i);
            }
        }
    }

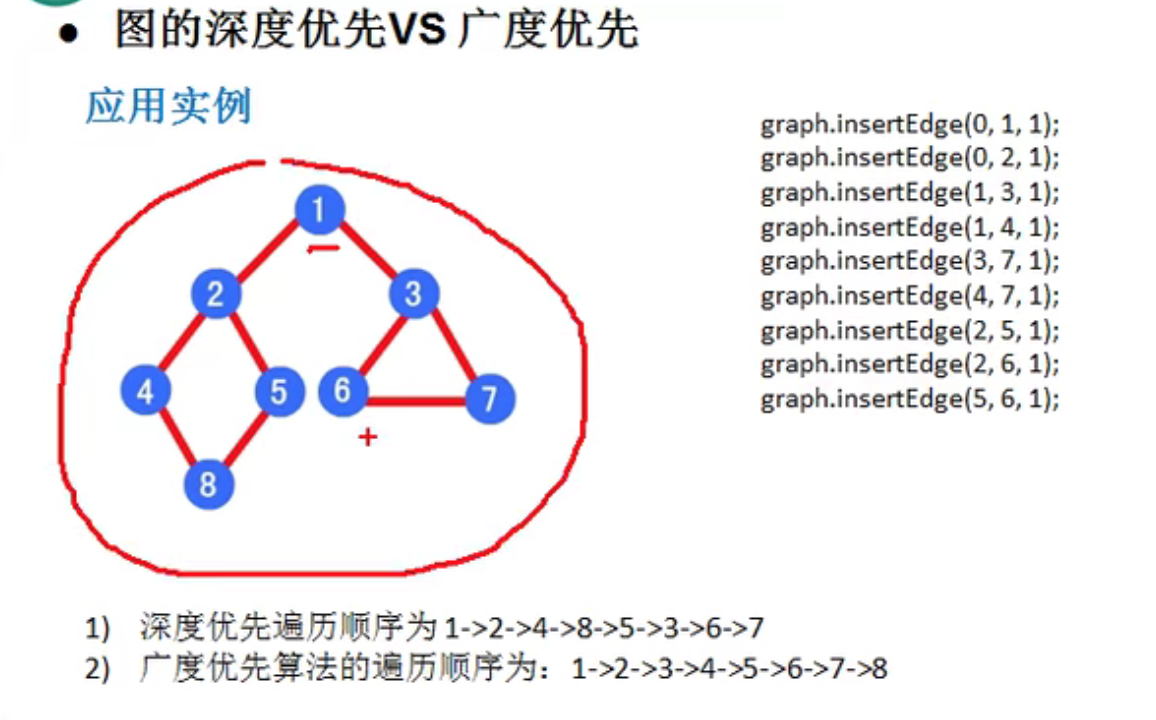
3、dfs与bfs之间的比较

4、图的总结

1、根据图的图形，创建邻接矩阵

2、dfs。回朔+递归 纵向

3、bfs。队列。横向