数据结构

1 链表是数据结构之一，其中的数据呈线性排列。在链表中，数据一般都是分散存储于内存中,无需存在在连续的空间内,所以数据的添加和删除都较为方便，就是访问比较耗费时间。

 

 

特殊的链表:循环链表,环形链表

循环链表

 

 

环形链表

 

 

2 数组也是数据呈线性排列的一种数据结构。与前一节中的链表不同，在数组中，访问数据十分
简单，而添加和删除数据比较耗工夫。

 

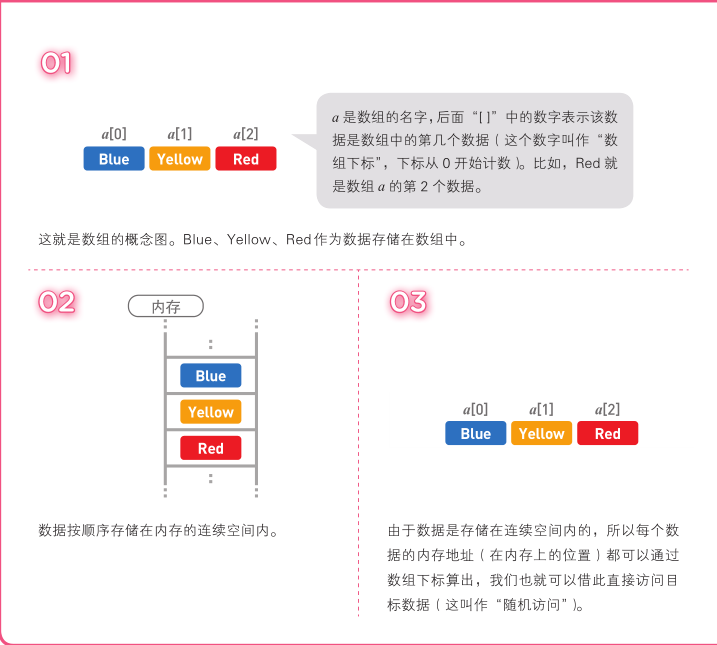
 链表和数组的区别:

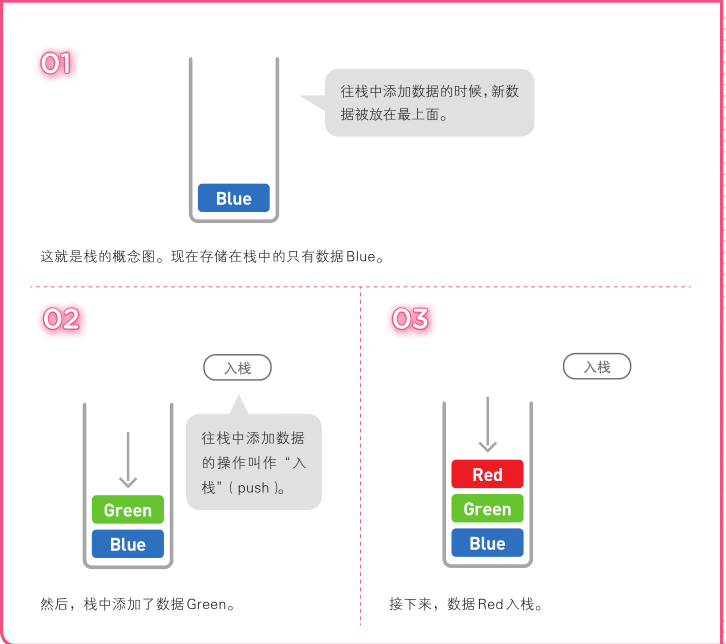
 3 栈也是一种数据呈线性排列的数据结构，不过在这种结构中，我们只能访问最新添加的数
据。栈就像是一摞书，拿到新书时我们会把它放在书堆的最上面，取书时也只能从最上面的新
书开始取。

与链表和数组一样，栈的数据也是线性排列，但在栈中，添加和删除数据的操作只
能在一端进行，访问数据也只能访问到顶端的数据。想要访问中间的数据时，就必须通
过出栈操作将目标数据移到栈顶才行。

 

  4 队列 与前面提到的数据结构相同，队列中的数据也呈线性排列。虽然与栈有些相似，但队列中
添加和删除数据的操作分别是在两端进行的。就和“队列”这个名字一样，把它想象成排成一
队的人更容易理解。在队列中，处理总是从第一名开始往后进行，而新来的人只能排在队尾。

 

 5 哈希表

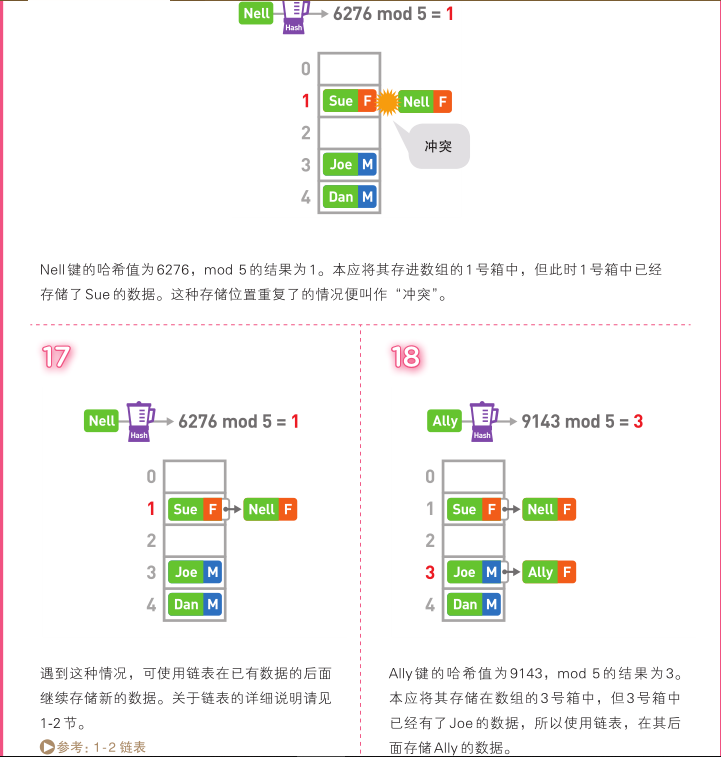
在哈希表中，我们可以利用哈希函数快速访问到数组中的目标数据。如果发生哈希
冲突，就使用链表进行存储。这样一来，不管数据量为多少，我们都能够灵活应对。
如果数组的空间太小，使用哈希表的时候就容易发生冲突，线性查找的使用频率也
会更高；反过来，如果数组的空间太大，就会出现很多空箱子，造成内存的浪费。因此，
给数组设定合适的空间非常重要。

 

 

5堆 堆是一种图的树形结构，被用于实现“优先队列”（priority queues）（树形结构的详细讲解
在 4-2 节）。优先队列是一种数据结构，可以自由添加数据，但取出数据时要从最小值开始按顺
序取出。在堆的树形结构中，各个顶点被称为“结点”（node），数据就存储在这些结点中。

特点: 1 堆中的每个结点最多有两个子结点。

　　  2 子结点必定大于父结点。

         3 取出数据后需要将最后的数据移到最顶端

 

 

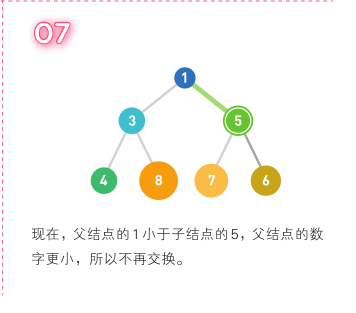
堆中最顶端的数据始终最小，所以无论数据量有多少，取出最小值的时间复杂度都
为 O(1)。
另外，因为取出数据后需要将最后的数据移到最顶端，然后一边比较它与子结点数据
的大小，一边往下移动，所以取出数据需要的运行时间和树的高度成正比。假设数据量为
n，根据堆的形状特点可知树的高度为 log 2 n ，那么重构树的时间复杂度便为 O(logn)。
添加数据也一样。在堆的最后添加数据后，数据会一边比较它与父结点数据的大
小，一边往上移动，直到满足堆的条件为止，所以添加数据需要的运行时间与树的高度
成正比，也是 O(logn)。

6 二叉树查找

二叉查找树（又叫作二叉搜索树或二叉排序树）是一种数据结构，采用了图的树形结构

二叉查找树有两个性质。第一个是每个结点的值均大于其左子树上任意一个结点的值

　                                   第二个是每个结点的值均小于其右子树上任意一个结点的值。

 

 根据这两个性质可以得到以下结论。首先，二
叉查找树的最小结点要从顶端开始，往其左下
的末端寻找。此处最小值为3。

反过来，二叉查找树的最大结点要从顶端开
始，往其右下的末端寻找。此处最大值为28。