国密 SM2 的非对称加密解密过程
国密 SM2 的非对称加密解密过程
国密 SM2 的非对称加密解密过程
椭圆曲线
椭圆曲线是由一组方程描述的点的集合：
y2 = x3 + ax + b 其中 a, b 满足 (4a3 + 27b2 ≠ 0)
SM2 定义了一个 sm2p256v1 的椭圆曲线方程
各种参数
BigInteger p = FromHex("FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF");
BigInteger a = FromHex("FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC");
BigInteger b = FromHex("28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93");
BigInteger n = FromHex("FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123");
BigInteger h = BigInteger.One;
Point G coord: (22963146547237050559479531362550074578802567295341616970375194840604139615431, 85132369209828568825618990617112496413088388631904505083283536607588877201568)
公钥，私钥
- 私钥：
可以随机生成一个 BigInteger D，必须符合区间 [1, n - 1]
- 公钥：
私钥 D * G(Point) 得到的一个 Point: Q
隐函数微分 dy/dx = (3x² + a) / (2y)
椭圆曲线密码（Elliptic Curve Cryptography，ECC）的安全性主要基于椭圆曲线离散对数问题（Elliptic Curve Discrete Logarithm Problem，ECDLP）的难度。简单来说，如果知道椭圆曲线上的两个点P和Q，并且知道存在一个整数d，使得dP=Q（这里的乘法表示点的数乘，就是把点P加d次），那么想从P和Q推算出d是几乎不可能的。这就是椭圆曲线离散对数问题。
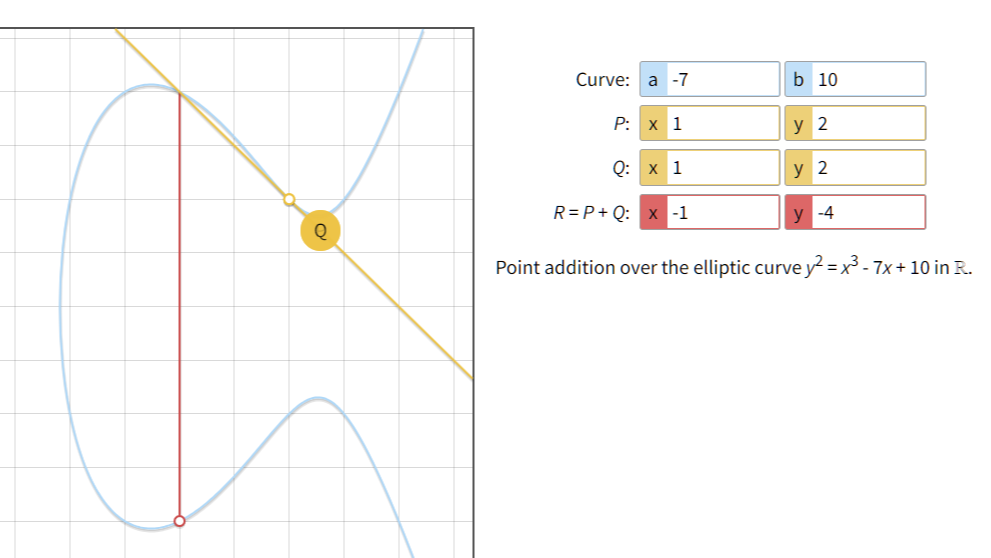
这个乘法异常的复杂 D * G 就是 D 个 G点相加，2 * G 就是过这个点的切线与椭圆曲线的交点，和 x 轴的对称点，还有有限域的处理，求同余...。
所以也能看出来知道公钥和 G 也很难求出 私钥 D
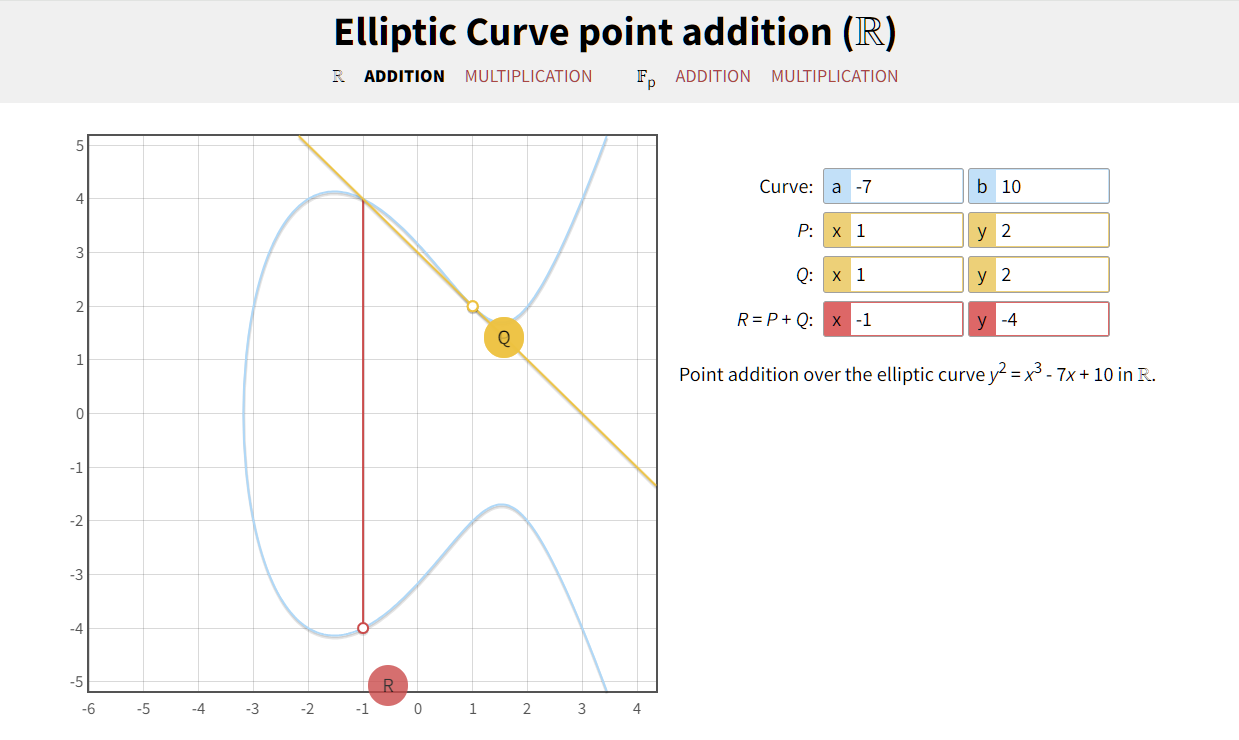
私钥和公钥的关系：
D * G = Q
加密过程
公钥： Q
- 随机生成一个 BigInteger K
- K * Q 生成一个 Point(x, y) KPB
C2: 每对原文 byte[] 每32个byte z循环处理，序号初始为1
32 和后续待处理字节长度取小值
- 对 KPB(x,y), 序号做摘要 记作 buf: byte[32]
- 这32个字节 分别和 buf的32个字节做异或运算 z[zOff + i] ^= buf[xOff + i];
- 序号 + 1 处理后续的
C1: k * G
C3: KPB.x 原文byte[], KPB.y 做摘要
解密过程
私钥: D
因为：C1 = K * G
所以 C1 * D = K * G * D = K * (G * D) = K * Q = KPB
然后: 异或运算满足 A ^ B ^ A = B
所以对 C2来相同的运算即可得到原文
C3用来验证是否一致
总结
知道密文和公钥无法解密，因为不知道随机生成的 K
C1 部分的生成和公私钥的生成是一模一样的，类似的原理很难通过 C1 和 G 倒推出K，解不了密
加密后占用空间 C2 和原文长度一致
C1 不压缩 标志位 + x + y = 65, C3 = 摘要长度 32 增大 97
C1 压缩 标志位 + x = 33 C3 = 摘要长度 32 增大 65
然后一般的结果有 C1C2C3 和 C1C3C2两种排列模式
实际情况中，针对这三部分有无数种基于 ASN.1 的包装方式，最终都是按照 C1C2C3 组装好进行解密
