算法的时间复杂度
时间复杂度的定义
在计算机科学中,时间复杂性,又称时间复杂度,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况。
我们把 算法需要执行的运算次数 用 输入大小n 的函数 表示,即 T(n) 。此时为了 估算算法需要的运行时间 和 简化算法分析,我们引入时间复杂度的概念。
时间复杂度的计算
存在常数 c 和函数 f(N),使得当 N >= c 时 T(N) <= f(N),表示为 T(n) = O(f(n)) 。因为f(n) 的增长速度是大于或者等于 T(n) 的,即T(n) = O(f(n)),所以我们可以用 f(n) 的增长速度来度量 T(n) 的增长速度,所以我们说这个算法的时间复杂度是 O(f(n))。
那么当我们拿到算法的执行次数函数 T(n) 之后怎么得到算法的时间复杂度呢?
- 我们知道常数项对函数的增长速度影响并不大,所以当 T(n) = c,c 为一个常数的时候,我们说这个算法的时间复杂度为 O(1);如果 T(n) 不等于一个常数项时,直接将常数项省略。
- 我们知道高次项对于函数的增长速度的影响是最大的。n^3 的增长速度是远超 n^2 的,同时 n^2 的增长速度是远超 n 的。 同时因为要求的精度不高,所以我们直接忽略低此项。
- 因为函数的阶数对函数的增长速度的影响是最显著的,所以我们忽略与最高阶相乘的常数。
时间复杂度的分类
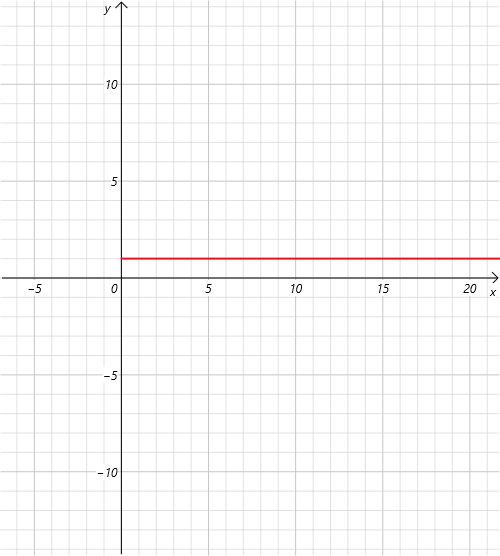
常数阶 O(1)
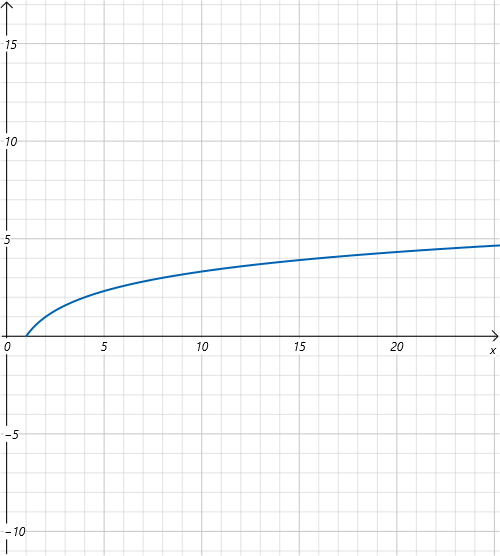
对数阶 O(logN)
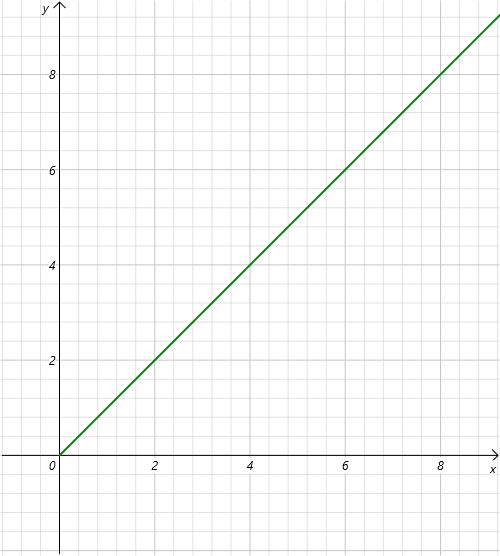
线性阶 O(N)
线性对数阶 O(NlogN)
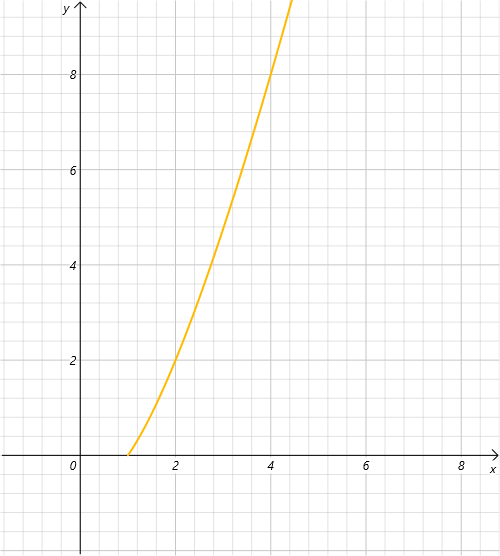
平方阶 O(N^2)
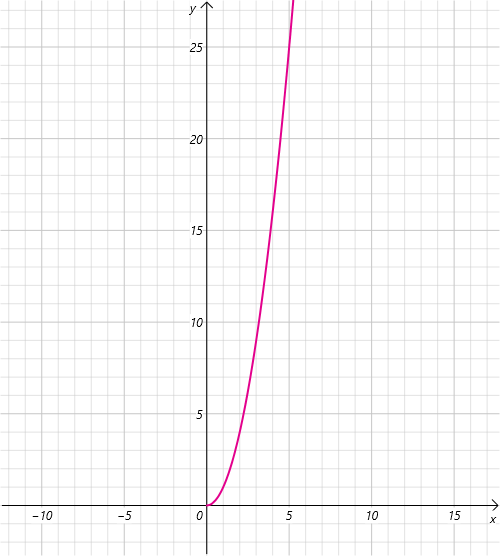
立方阶 O(N^3)
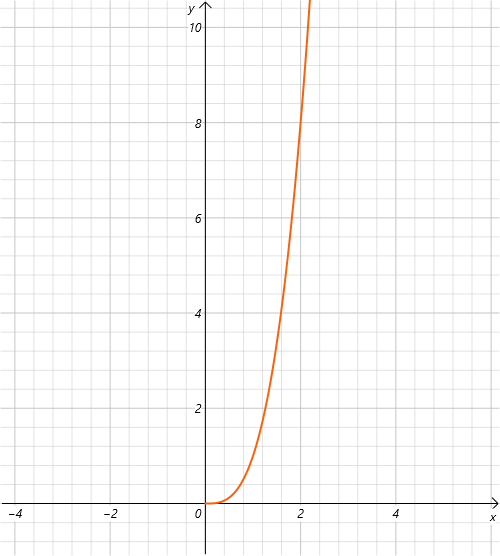
指数阶 O(2^N)
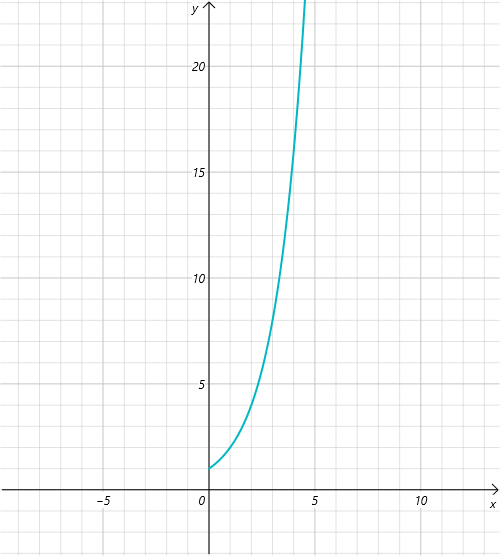
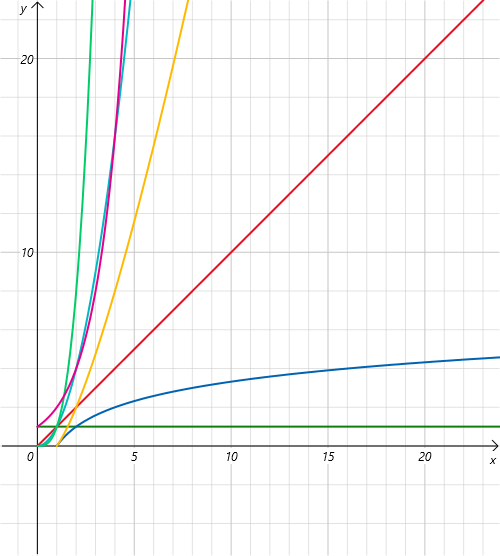
总结
就是这张霸气外露的图