1 Recurrent Neural Networks(循环神经网络)
1.1 序列数据
输入或输出其中一个或两个是序列构成。例如语音识别,自然语言处理,音乐生成,感觉分类,dna序列,机器翻译,视频状态识别,名称识别。
1.2 Notation(符号)
\(x ^ { ( i ) < t > }\)表示第\(i\)个训练样本输入的第\(t\)个元素
\(T ^ { ( i ) < t > } _ x\)表示第\(i\)个训练样本输入的长度为\(t\)
\(y ^ { ( i ) < t > }\)表示第\(i\)个训练样本输出的第\(t\)个元素
\(T ^ { ( i ) < t > } _ y\)表示第\(i\)个训练样本输出的长度为\(t\)
使用one-hot方式表示单词。有一个单词编号的词组,使用一个只有一个1的向量表示每个单词。
1.3 Recurrent Neural Network Model(循环神经网络)
1.3.1 为什么不用标准的神经网络
- 输入输出可能不同长度
- 标准神经网络不会将不同文本位置学到的特征进行共享
- 会有大量的参数需要训练(自己总结的,吴恩达没有列出来,但是讲了)
1.3.2 循环神经网络的前向传播
循环神经网络的网络图一般有两种画法,第一种是展开画的,第二种是画成循环的,两种都可以,课程中吴恩达选择画展开的。
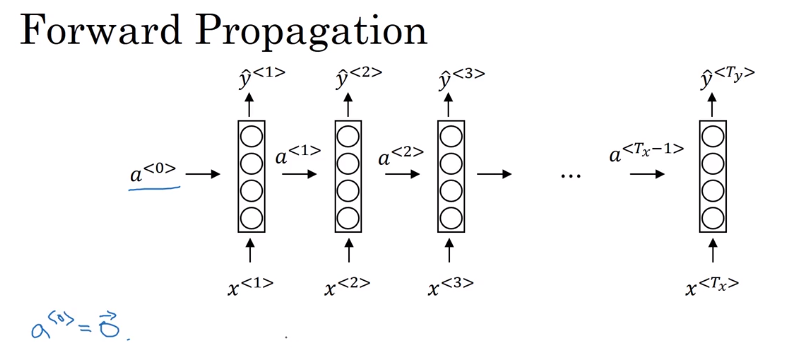
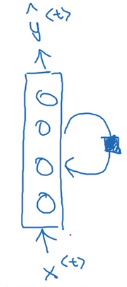
其中一个参数取值\(a^{<0>}=\vec 0\),也有人取随机值。
另外还有三个参数,\(W _ {aa}\)表示输入为\(a\),输出为\(a\)的参数。剩下的\(W_{ax}、W_{ya}\)的定义一样。在网络种每个对应位置都使用相同的参数。
前向计算公式,\(a^{<t>}\)的激活函数最常使用tanh,也使用relu。\(\hat y ^{<t>}\)根据输出要求,例子里的名字判断是个二分,就是用sigmoid。
\[a ^ { < t > } = g \left( W _ { a a } a ^ { < t - 1 > } + W _ { a x } x ^ { < t > } + b _ { a } \right)
\]
\[\hat { y } ^ { < t > } = g \left( W _ { y a } a ^ { < t > } + b _ { y } \right)
\]
为了便于构造复杂的网络,简化公式表示:
\[a ^ { \langle t \rangle } = g \left( w _ { a } \left[ a ^ { ( t - 1 ) } , x ^ { ( t ) } \right] + b _ { a } \right)
\]
\[\hat { y } ^ { < t > } = g \left( W _ { y } a ^ { < t > } + b _ { y } \right)
\]
其中
\[W_a=\left[\begin{matrix}W_{aa} & W_{ax}\end{matrix}\right]
\]
\[\left[ a ^ { ( t - 1 ) } , x ^ { ( t ) } \right]=\left[\begin{matrix} a^{<t-1>}\\x^{<t>} \end{matrix}\right]
\]
1.3.3 计算图(Computational Graph)
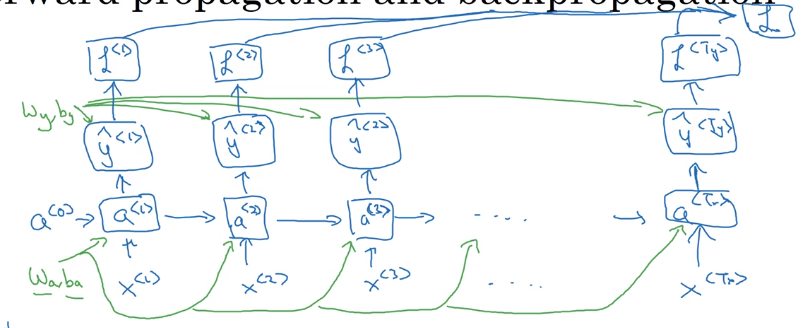
1.3.4 损失函数(Loss function)
\[L^{<t>}(\hat y^{<t>},y^{<t>})=-y^{<t>}log(\hat y^{<t>})-(1-y^{<t>})log(1-\hat y^{<t>})
\]
\[L(\hat y,y)=\sum ^{T_y}_{t=1}L^{<t>}(\hat y^{<t>},y^{<t>})
\]
1.4 循环神经网络的反向传播
这个方法也叫,Backpropagation through time。因为反向传播是反着时序走的。
有了前面的前向传播的计算图,就能计算反向传播了。
根据课后题补充的反向传播内容:
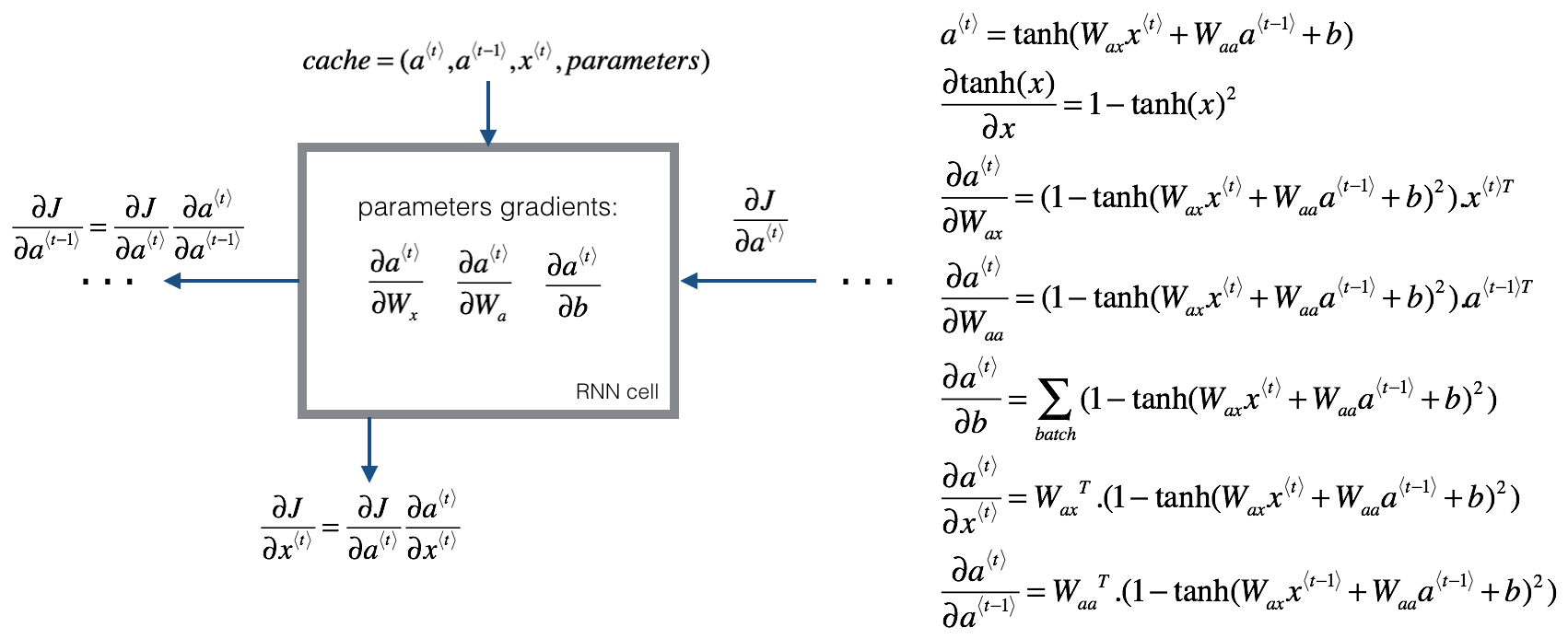
\[a ^ { \langle t \rangle } = \tanh \left( W _ { a x } x ^ { ( t ) } + W _ { a a } a ^ { \langle t - 1 \rangle } + b \right)
\]
\[\frac { \partial \tanh ( x ) } { \partial x } = 1 - \tanh ( x ) ^ { 2 }
\]
\[\frac { \partial a ^ { ( t ) } } { \partial W _ { a x } } = ( 1 - \tanh ( W _ { a x } x ^ { ( t ) } + W _ { a a } a ^ { ( t - 1 ) } + b ) ^ { 2 }) x ^ { ( t ) T }
\]
\[\frac { \partial a ^ { ( t ) } } { \partial W _ { a a } } = ( 1 - \tanh ( W _ { a x } x ^ { ( t ) } + W _ { a a } a ^ { ( t - 1 ) } + b ) ^ { 2 } ) a ^ { ( t - 1 ) T }
\]
\[\frac { \partial a ^ { ( t ) } } { \partial b } = \sum _ { b a c c h } ( 1 - \tanh ( W _ { a x } x ^ { ( t ) } + W _ { a a } a ^ { ( t - 1 ) } + b ) ^ { 2 } )
\]
\[\frac { \partial a ^ { ( t ) } } { \partial x ^ { ( t ) } } = W _ { a x } ^ { T } ( 1 - \tanh ( W _ { a x } x ^ { ( t ) } + W _ { a a } a ^ { ( t - 1 ) } + b ) ^ { 2 } )
\]
\[\frac { \partial a ^ { ( t ) } } { \partial a ^ { ( t - 1 ) } } = W _ { a a } ^ { T } ( 1 - \tanh ( W _ { a x } x ^ { ( t - 1 ) } + W _ { a a } a ^ { ( t - 1 ) } + b ) ^ { 2 } )
\]
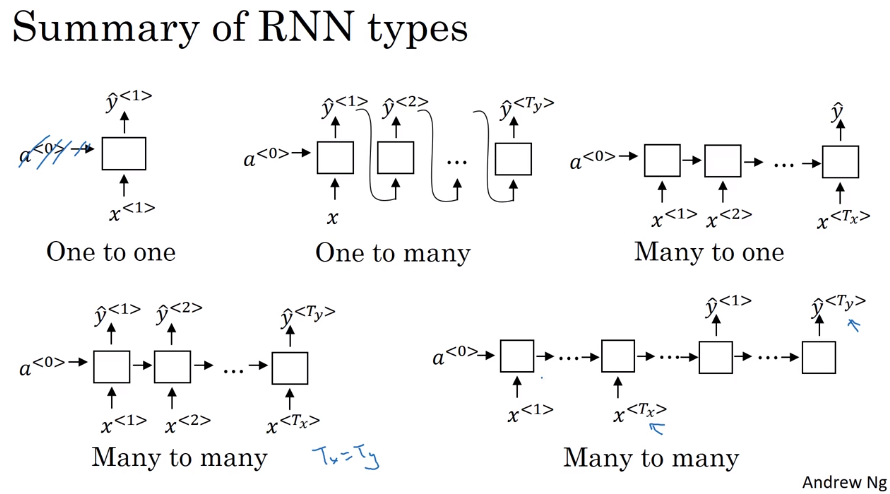
1.5 不同种类的RNN
- many to many。每一个块都输出。输入输出个数相同
- many to one。只有最后一个块有输出。例子,输出评分/感觉。
- one to many。只有第一个块有输入。实际上会将前一个块的输出输入给后一块。
- many to many。输入输出不同。一个只输入的接上一个只输出的。
- one to one。标准神经网络。
1.6 Language model and sequence generation(语言模型和序列生成)
1.6.2 语言模型
输入一句话,输出这句话出现的概率。具体是指你随机的听到/读到某句话,下一句话是输入的这句话的概率。语言模型的输入被记作\(y^{<1>},y^{<2>},...,y^{<T_y>}\),因为语言模型通常被用作输出句子,用来估计特定词序列的概率。
1.6.1 使用RNN建立语言模型
训练集:large corpus of english text.(大文集构成的训练集)
tokenize(标记化)。将每一个词对应字典索引,使用one-hot。对于字典里没有的单词使用UNK,句子的结尾使用EOS。
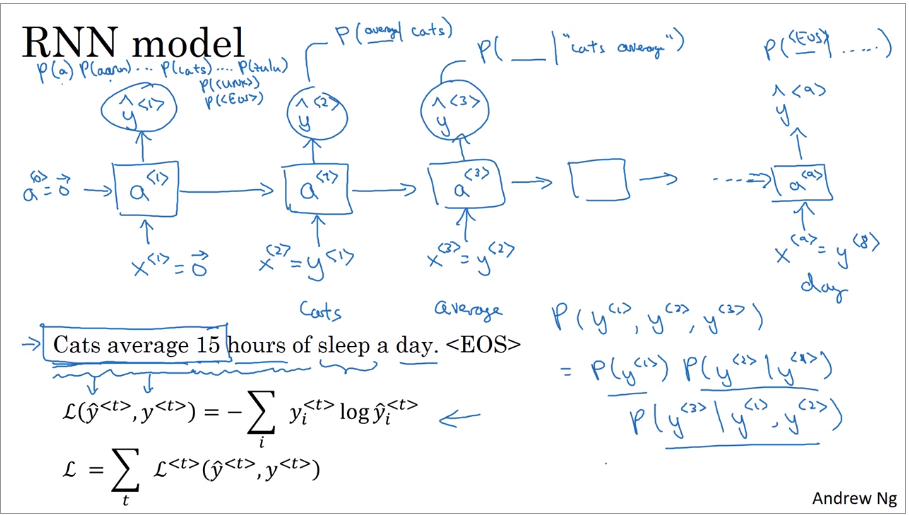
rnn中,\(x^{<1>}=\vec 0\),\(a^{<0>}=\vec 0\)。\(\hat y ^{<1>}\)使用softmax输出字典表中每一个单词的概率。\(x^{<t>}=y^{<t-1>}\),第二个块使用正确的句子中的第一个输入,输出\(y^{<2>}\)是在第一个单词为cats情况下的其他单词的概率(\(P(\_|cats)\)),还使用softmax。第三个是在cats average下的概率(\(P(\_|cats\ average)\))。
loss function使用softmax的。
\[L \left( \hat { y } ^ { < t > } , y ^ { < t > } \right) = - \sum _ { i } y _ { i } ^ { < t > } \log \hat { y } _ { i } ^ { < t > }
\]
\[L = \sum _ { t } L ^ { < t > } \left( \hat { y } ^ { < t > } , y ^ { < t > } \right)
\]
当计算一个句子的概率时,相当于计算每个词在前面词出现后的概率相乘。
\[P ( y ^ { < 1 > } , y ^ { < 2 > } , y ^ { < 3 > } ) = P ( y ^ { < 1 > })P ( y ^ { < 2 > } | y ^ { < 1 > }) P ( y ^ { < 3 > } | y ^ { < 1 > } , y ^ { < 2 > } )
\]
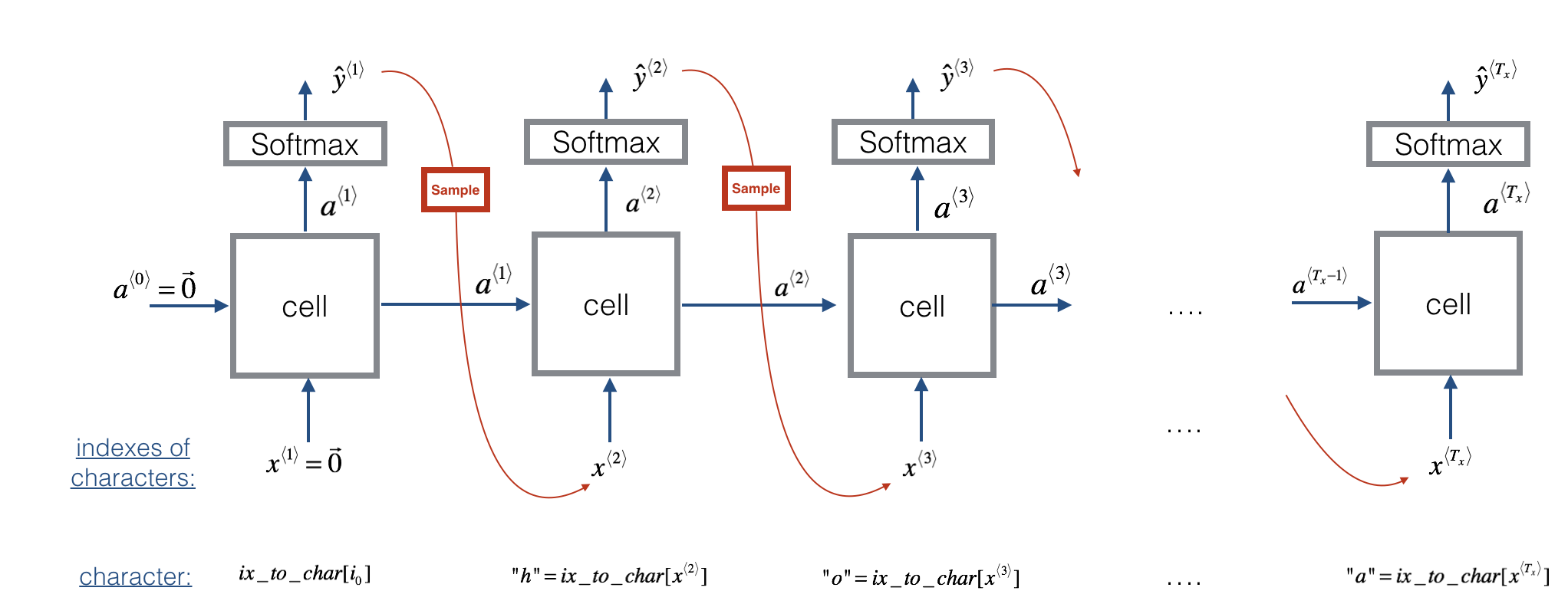
吴恩达上课手画的还是让我理解出现了些偏差,这里再放上课程作业里的图,这个图更加的清晰,让我知道在哪个地方sample。图中的cell可以使用RNN/GRU/LSTM。其中的公式如下。
\[a^{\langle t+1 \rangle} = \tanh(W_{ax} x^{\langle t \rangle } + W_{aa} a^{\langle t \rangle } + b)
\]
\[z^{\langle t + 1 \rangle } = W_{ya} a^{\langle t + 1 \rangle } + b_y
\]
\[\hat{y}^{\langle t+1 \rangle } = softmax(z^{\langle t + 1 \rangle })
\]
sample使用的python代码:
np.random.choice(range(vocab_size), p = y.ravel())
1.7 Sampling novel sequences(采样)
在一个训练好的RNN语言模型上,第一个输入为\(\vec 0\),会有一个softmax输出,表示每个单词的概率,使用softmax的分布去随机采样,得到一个输出\(\hat y\),然后给下一循环做输入,循环。出现EOS或者输出个数超过设定的N个词后结束。出现UNK可以重新采样,也可以就放在里面。
从字母层面的语言模型。不使用单词,使用字母。训练的时候也要用字母。优势是不需要担心不认识的单词,劣势是会是序列变长,更多的算力。
1.8 Vanishing/Exploding gradients with RNNs(梯度消失)
1.8.1 梯度消失
语言中一个单词可能会影响很多单词之后出现的单词。例如单复数对应的be动词。但是RNN在传播中会遇到梯度爆炸或梯度消失问题,导致RNN不能很好的处理这个。梯度消失比梯度爆炸更难解决,可以使用GRU/LSTM解决。
1.8.2 梯度爆炸
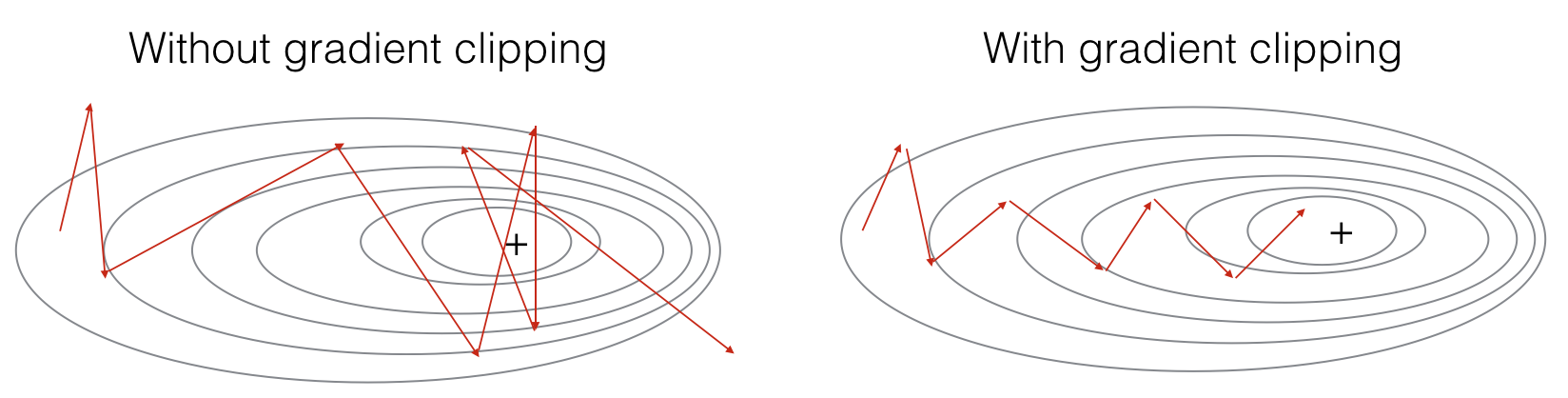
RNN也会出现梯度爆炸,但是这个很容易被察觉,出现NaN。对于梯度爆炸,可以使用gradient clipping解决,clipping就是个限幅。当梯度超过某个最大阈值或低于最小阈值,使其等于最大/最小。
1.9 Gated Recurrent Unit(GRU)
1.9.1 标准RNN
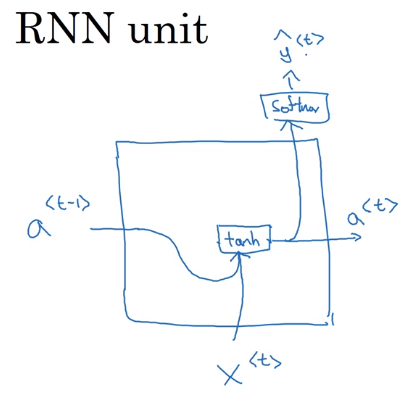
标准RNN的单元可以使用下面的图描述。
\[a ^ { < t > } = g \left( W _ { a } \left[ a ^ { < t - 1 > } , x ^ { < t > } \right] + b _ { a } \right)
\]
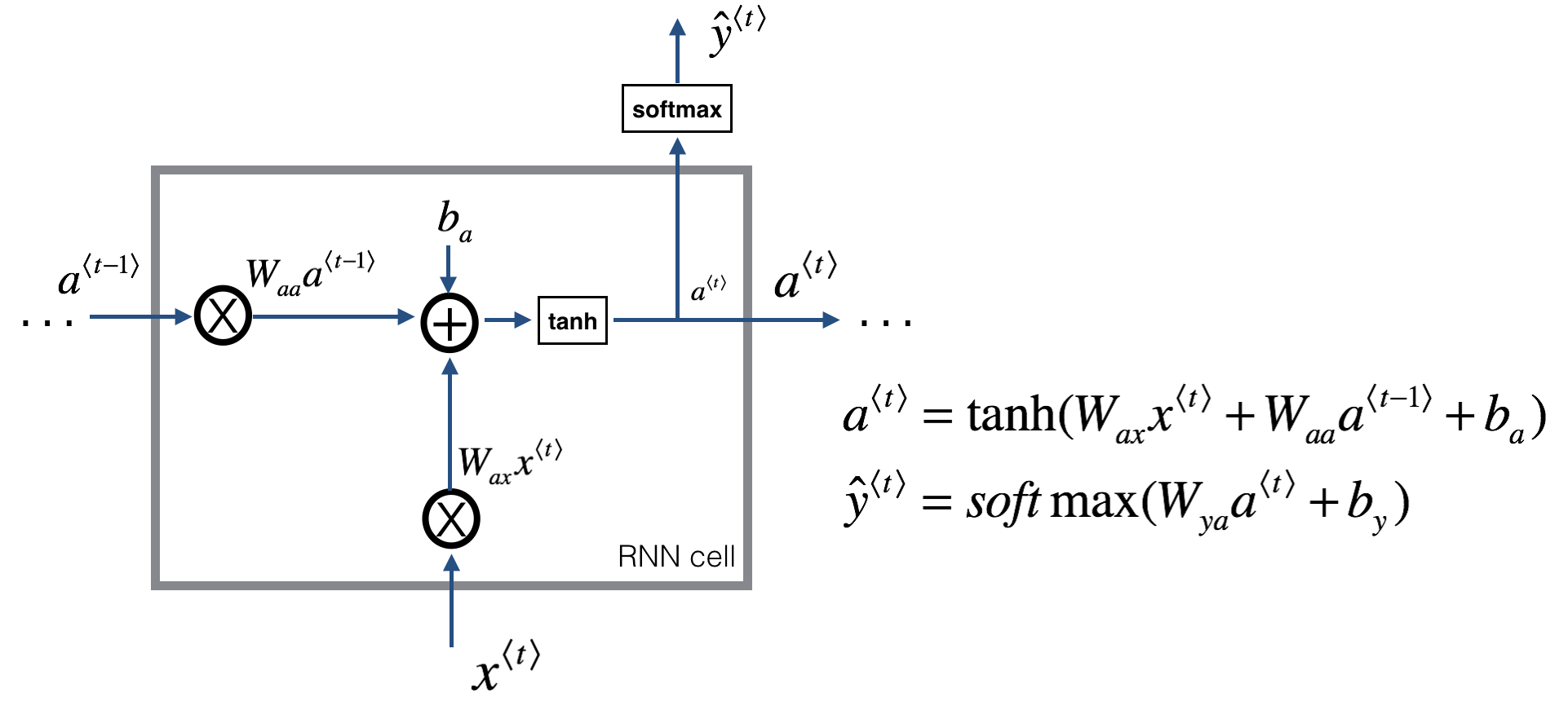
课后题里的图和公式:
\[\begin{array} { l } { a ^ { ( t ) } = \tanh \left( W _ { a x } x ^ { ( t ) } + W _ { a a } a ^ { ( t - 1 ) } + b _ { a } \right) } \\ { \hat { y } ^ { ( t ) } = s o f t \max \left( W _ { y a } a ^ { ( t ) } + b _ { y } \right) } \end{array}
\]
1.9.2 简化的GRU
引入一个c(memory cell),实际上就是原来的a。
\[c^{<t>}=a^{<t>}
\]
然后引入一个c的候选人\(\tilde c\)。
\[\tilde c^{<t>}=tanh(W_c[c^{<t-1>},x^{<t>}]+b_c)
\]
一个门(gate)\(\Gamma _ u\),数值在0-1之间。但是一般都是很接近0或者很接近1。使用sigmoid函数。sigmoid的参数一般都比较大,所以很接近0或1。gate决定是否使用\(\tilde c\)更新\(c\)。
\[\Gamma_u=\sigma(W_u[c^{<t-1>},x^{<t>}]+b_u)
\]
\(c^{<t>}\)的更新
\[c^{<t>}=\Gamma_u * \tilde c^{<t>}+(1-\Gamma_u)*c^{<t-1>}
\]
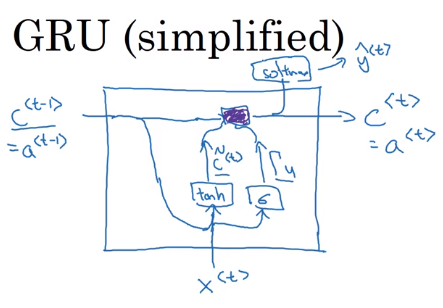
GRU的结构图如下所示,紫色部分代表了\(c^{<t>}\)的更新。GRU能够保留部分的内容。而且因为gate使用了sigmoid,所以对于要保留记忆部分的gate\(\Gamma_u\)将很小很小,例如0.00001,所以在更新\(c^{<t>}\)时不会出现梯度消失的问题。所以RNN可以经过很多很多步。在实际中\(c^{<t>}\)是个向量,能保留许多不同的内容,\(\Gamma_u\)和\(\tilde c^{<t>}\)也是个向量。更新\(c^{<t>}\)的乘法是元素相乘。
1.9.3 full GRU
实际使用中还有一个门\(\Gamma_r\),可以认为它表示相关性。
\[\tilde c^{<t>}=tanh(W_c[\Gamma_r*c^{<t-1>},x^{<t>}]+b_c)
\]
\[\Gamma_u=\sigma(W_u[c^{<t-1>},x^{<t>}]+b_u)
\]
\[\Gamma_r=\sigma(W_r[c^{<t-1>},x^{<t>}]+b_r)
\]
\[c^{<t>}=\Gamma_u * \tilde c^{<t>}+(1-\Gamma_u)*c^{<t-1>}
\]
论文人们常用,\(\tilde h\)表示\(\tilde c^{<t>}\),\(u\)表示\(\Gamma_u\),r表示\(\Gamma_r\),\(h\)表示\(c^{<t>}\)。吴恩达在课程中这么表示是为了统一和LSTM的公式,更便于理解。
1.10 Long Short Term Memory (LSTM)
1.10.1 前向传播
LSTM使用了三个门,遗忘(forgot)、更新(update)、输出(output),并且\(c \neq a\)。
\[\begin{array} { l } { \tilde { c } ^ { < t > } = \tanh \left( W _ { c } \left[ a ^ { < t - 1 > } , x ^ { < t > } \right] + b _ { c } \right) } \\ { \Gamma _ { u } = \sigma \left( W _ { u } \left[ a ^ { < t - 1 > } , x ^ { < t > } \right] + b _ { u } \right) } \\ { \Gamma _ { f } = \sigma \left( W _ { f } \left[ a ^ { < t - 1 > } , x ^ { < t > } \right] + b _ { f } \right) } \\ { \Gamma _ { o } = \sigma \left( W _ { o } \left[ a ^ { < t - 1 > } , x ^ { < t > } \right] + b _ { o } \right) } \\ { c ^ { < t > } = \Gamma _ { u } * \tilde { c } ^ { < t > } + \Gamma _ { f } * c ^ { < t - 1 > } } \\ { a ^ { < t > } = \Gamma _ { o } * \tanh c ^ { < t > } } \end{array}
\]
LSTM的结构图如下。使用时将多个单元串联就行。LSTM这里c单独一条先来传递。LSTM/GRU能够很好的记忆,因为c一直在传递。
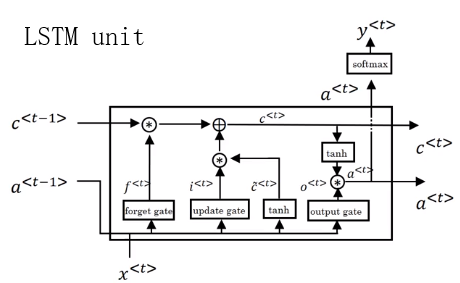
LSTM有很多变种,其中一个peephole connection(窥孔链接),窥孔连接中,同时将c加入到门的求解中,每个c只会影响相对应的门变量的值。
LSTM和GRU先用哪个没有明确的结果,但是吴恩达认为GRU更简单,构造更大的网络很简单,因为只有两个门,从计算的角度看更高效;LSTM更强大更有效,是经过历史检验的方法,被很多人作为默认。GRU也在快速发展,很多团队都在使用。使用这两个都可以构造更深的神经网络。
1.10.2 反向传播
反向传播在吴恩达课程的练习中算的是不对的,这里复制了社区的内容。我还没有自己求解。
The LSTM backward pass is slighltly more complicated than the forward one. We have provided you with all the equations for the LSTM backward pass below. (If you enjoy calculus exercises feel free to try deriving these from scratch yourself.)
gate derivatives
\[d \Gamma_o^{\langle t \rangle} = da_{next}*\tanh(c_{next}) * \Gamma_o^{\langle t \rangle}*\left(1-\Gamma_o^{\langle t \rangle}\right)\tag{7}
\]
\[d\widetilde{c}^{\langle t \rangle} = \left(dc_{next}*\Gamma_u^{\langle t \rangle}+ \Gamma_o^{\langle t \rangle}* (1-\tanh(c_{next})^2) * \Gamma_u^{\langle t \rangle} * da_{next} \right) * \left(1-\left(\widetilde c^{\langle t \rangle}\right)^2\right) \tag{8}
\]
\[d\Gamma_u^{\langle t \rangle} = \left(dc_{next}*\widetilde{c}^{\langle t \rangle} + \Gamma_o^{\langle t \rangle}* (1-\tanh(c_{next})^2) * \widetilde{c}^{\langle t \rangle} * da_{next}\right)*\Gamma_u^{\langle t \rangle}*\left(1-\Gamma_u^{\langle t \rangle}\right)\tag{9}
\]
\[d\Gamma_f^{\langle t \rangle} = \left(dc_{next}* c_{prev} + \Gamma_o^{\langle t \rangle} * (1-\tanh(c_{next})^2) * c_{prev} * da_{next}\right)*\Gamma_f^{\langle t \rangle}*\left(1-\Gamma_f^{\langle t \rangle}\right)\tag{10}
\]
parameter derivatives
\[dW_f = d\Gamma_f^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{11}
\]
\[dW_u = d\Gamma_u^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{12}
\]
\[dW_c = d\widetilde c^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{13}
\]
\[dW_o = d\Gamma_o^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{14}
\]
To calculate \(db_f, db_u, db_c, db_o\) you just need to sum across the horizontal (axis= 1) axis on \(d\Gamma_f^{\langle t \rangle}, d\Gamma_u^{\langle t \rangle}, d\widetilde c^{\langle t \rangle}, d\Gamma_o^{\langle t \rangle}\) respectively. Note that you should have the keep_dims = True option.
Finally, you will compute the derivative with respect to the previous hidden state, previous memory state, and input.
\[da_{prev} = W_f^T d\Gamma_f^{\langle t \rangle} + W_u^T d\Gamma_u^{\langle t \rangle}+ W_c^T d\widetilde c^{\langle t \rangle} + W_o^T d\Gamma_o^{\langle t \rangle} \tag{15}
\]
Here, the weights for equations 15 are the first n_a, (i.e. \(W_f = W_f[:,:n_a]\) etc...)
\[dc_{prev} = dc_{next}*\Gamma_f^{\langle t \rangle} + \Gamma_o^{\langle t \rangle} * (1- \tanh(c_{next})^2)*\Gamma_f^{\langle t \rangle}*da_{next} \tag{16}
\]
\[dx^{\langle t \rangle} = W_f^T d\Gamma_f^{\langle t \rangle} + W_u^T d\Gamma_u^{\langle t \rangle}+ W_c^T d\widetilde c^{\langle t \rangle} + W_o^T d\Gamma_o^{\langle t \rangle}\tag{17}
\]
where the weights for equation 17 are from n_a to the end, (i.e. \(W_f = W_f[:,n_a:]\) etc...)
1.11 Bidirectional RNN(双向RNN)
有些内容只看过去的无法判断,例子中判断Teddy是否为名字,所以需要未来的信息。
在原始的RNN中,加入将未来数据向之前传播的过程(后向连接)。这不是反向传播,而是前向传播的一部分。结构如下图所示,紫色的为前向连接,绿色的为后向连接。图中的每个块可以是RNN、GRU、LSTM。最后输出变为如下形式。
\[\hat y^{<t>}=g(W_y[{\overset{\rightarrow}{a}}^{<t>},{\overset{\leftarrow}{a}}^{<t>}]+b_y)
\]
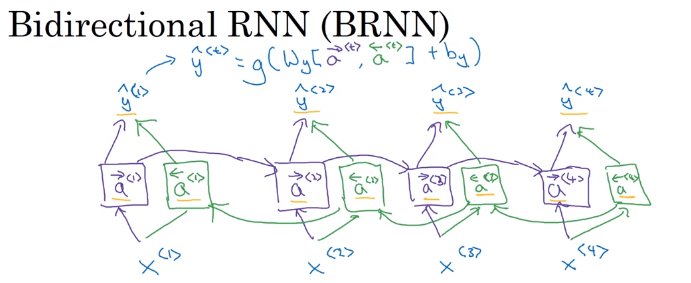
BRNN的缺点是需要整个句子才能做预测。
1.12 Deep RNNs
深度RNN就是将每一个块在纵向上增加层数。每一层公用一个权重W。因为RNN本来就要走很多步,已经算深度网络了,所以一般只再加上3层。结构图如下所示。
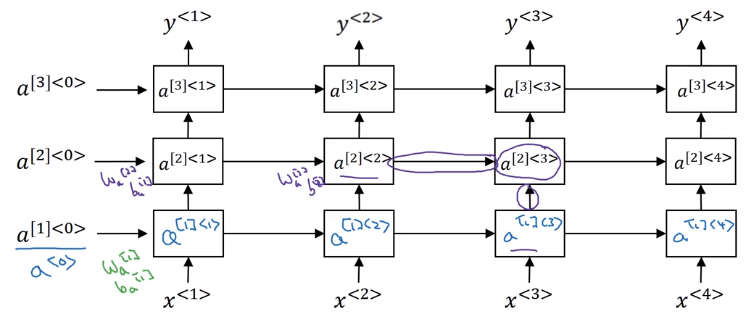
最后在输出层加上没有横向连接的深度网络也比较常见。















