【洛谷P3386】【模板】二分图匹配

题目背景

二分图

题目描述

给定一个二分图，结点个数分别为n,m，边数为e，求二分图最大匹配数

输入输出格式

输入格式：

第一行，n,m,e

第二至e+1行，每行两个正整数u,v，表示u,v有一条连边

输出格式：

共一行，二分图最大匹配

输入输出样例

输入样例#1：

1 1 1
1 1

输出样例#1：

1

说明

n,m≤1000，1≤u≤n，1≤v≤m

因为数据有坑，可能会遇到 v>m 的情况。请把 v>m 的数据自觉过滤掉。

算法：二分图匹配

分析

知识点：题目上都说了是二分图最大匹配。

本题不是很难，是个模板题，想借这个模板题说一说匈牙利算法。关于增广路，交替路网上的解释很多，这里默认读者已会。

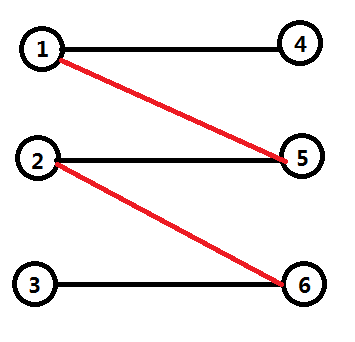
匈牙利算法是通过不断地寻找增广路来增加匹配数。如图3->6->2->5->1->4就是一个增广路，因为增广路的初边和终边都是非匹配边，所以增广路的非匹配边比匹配边多1个。

只要将匹配边变成非匹配边，非匹配边变成匹配边，这样的话匹配边就多了一个。

关键的是在于代码实现。

我们从非匹配点出发所走的边一定是非匹配边，如果所走到的点是非匹配点，那么我们就已经找到了一条增广路。

如果走到的是匹配点，我们要走的是交替路，所以下一次要走匹配边，假如i是匹配点，match[i]是i所匹配的点，那么i->match[i]一定是匹配边。

这样一直做下去，如果找到增广路return true否则return false。

还有一点二分图中可能会有偶环（不会有奇环的），所以要加一个vis数组来判断这个点是否被访问过。

代码

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=1000+5;
inline int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int n,m,e,ans;
int match[maxn];
bool mp[maxn][maxn],vis[maxn];
bool find(int x)
{
    for(int i=1;i<=m;i++)
    if(mp[x][i]&&!vis[i])
    {
        vis[i]=1;
        if(!match[i]||find(match[i]))
        {//如果找到了，就把非匹配边变成匹配边
            match[i]=x;
            return 1;
        }
    }
    return 0;
}
int main()
{
    n=read();m=read();e=read();
    for(int i=1;i<=e;i++)
    {
        int x,y;
        x=read();y=read();
        if(y>m) continue;
        mp[x][y]=1;//这儿是单向边
    }
    for(int i=1;i<=n;i++)
    {
        memset(vis,0,sizeof(vis));
        if(find(i)) ans++;
    }
    printf("%d\n",ans);
    return 0;
}