LeetCode 刷题 2021/10/15
LeetCode 刷题 2021/10/15
48. 旋转图像
题目
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
思路
题目要求不能用辅助数组。
易知原矩阵第 i 行,第 j 列的元素在旋转后变换到了第 j 行,第 n - i - 1 列。
- 先假设 n 为偶数:
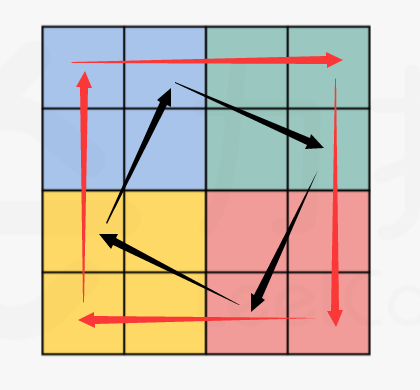
如图,每次变换只涉及到 4 个值,只要从 1/4 个正方形开始变换就能完成整个正方形的变换。
- 若 n 为 奇数:
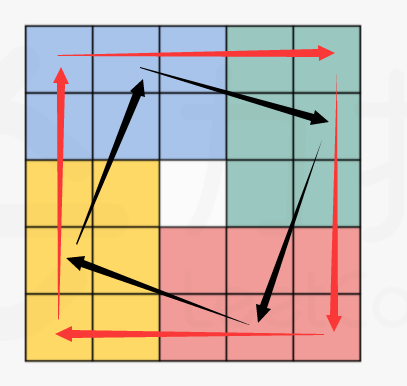
代码
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < (n+1)/2; j++) {
int temp = matrix[i][j];
matrix[i][j] = matrix[n-j-1][i];
matrix[n-j-1][i] = matrix[n-i-1][n-j-1];
matrix[n-i-1][n-j-1] = matrix[j][n-i-1];
matrix[j][n-i-1] = temp;
}
}
}
};
另一种思路
旋转 90 度等价于先水平翻转,再沿主对角线翻转。
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
// 水平翻转
for (int i = 0; i < n / 2; ++i) {
for (int j = 0; j < n; ++j) {
swap(matrix[i][j], matrix[n - i - 1][j]);
}
}
// 主对角线翻转
for (int i = 0; i < n; ++i) {
for (int j = 0; j < i; ++j) {
swap(matrix[i][j], matrix[j][i]);
}
}
}
};
49. 字母异位词分组
题目
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的字母得到的一个新单词,所有源单词中的字母都恰好只用一次。
思路
对每个字符串排序,再判断是否相同。
代码
class Solution {
public:
vector<vector<string>> groupAnagrams(vector<string>& strs) {
unordered_map<string, vector<string>> mp;
for (string& str: strs) {
string key = str;
sort(key.begin(), key.end());
mp[key].emplace_back(str);
}
vector<vector<string>> ans;
for (auto it = mp.begin(); it != mp.end(); it++) {
ans.emplace_back(it->second);
}
return ans;
}
};
50. Pow(x, n)
题目
实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,xn)。
思路
设整数 n > 0,
-
求 \(x^n\): 用快速幂
-
求 \(x^{-n}\):\(x^{-n}=\frac{1}{x^n}\)
class Solution {
public:
double ksm(double x, long long n) {
if (n == 0) return 1.0;
double ret = 1.0;
for ( ; n; n >>= 1, x*=x) {
if (n & 1) ret *= x;
}
return ret;
}
double myPow(double x, int n) {
long long N = n;
return n > 0 ? ksm(x, N) : 1.0 / ksm(x, -N);
}
};
欢迎转载,转载请注明出处!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号