2019.10.20周赛
A - Minimum Ternary String CodeForces - 1009B
签到题,数字1可以随便调位置,2和0的相对位置不变。

#include<cstdio> #include<cstring> using namespace std; char s[100010]; int main(){ scanf("%s",s); int n=strlen(s),cnt=0; bool flag=0; for(int i=0;i<n;++i) if(s[i]=='1') cnt++; for(int i=0;i<n;++i){ if(flag){ if(s[i]=='1') continue; printf("%c",s[i]); continue; } if(s[i]=='0') printf("0"); else if(s[i]=='1') continue; else if(s[i]=='2'){ for(int j=1;j<=cnt;++j) printf("1"); printf("2"); flag=1; } } if(!flag){ for(int i=1;i<=cnt;++i) printf("1"); } return 0; }
B - Equalize CodeForces - 1037C
还是签到题。当两个不同的数的距离大于1时,就直接变。

#include<cstdio> #include<cstring> using namespace std; const int N=1000010; int n,ans=0; char a[N],b[N]; bool df[N]; int main(){ scanf("%d",&n); scanf("%s%s",a,b); for(int i=0;i<n;++i) if(a[i]!=b[i]) df[i]=1; for(int i=0;i<n;++i){ if(df[i]==0) continue; if(b[i]=='0'){ if(b[i+1]=='1'&&df[i+1]){ ans++; df[i]=df[i+1]=0; }else{ ans++; df[i]=0; } }else if(b[i]=='1'){ if(b[i+1]=='0'&&df[i+1]){ ans++; df[i]=df[i+1]=0; }else { ans++; df[i]=0; } } } printf("%d\n",ans); return 0; }
C - Cut 'em all! CodeForces - 982C
考虑一个边能不能去掉,如果这个变两侧的点数都是偶数的话就可以去掉。

#include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int N=1000010; int n,cnt,hd[N],size[N],dep[N]; struct node{ int nxt,to; }e[N*2]; struct data{ int x,y; }a[N]; inline void ins(int from,int to){ e[++cnt].nxt=hd[from]; e[cnt].to=to; hd[from]=cnt; } void dfs(int x,int fa){ size[x]=1; for(int i=hd[x];i;i=e[i].nxt){ if(e[i].to==fa) continue; dep[e[i].to]=dep[x]+1; dfs(e[i].to,x); size[x]+=size[e[i].to]; } } int main(){ scanf("%d",&n); for(int i=1;i<n;++i){ scanf("%d%d",&a[i].x,&a[i].y); ins(a[i].x,a[i].y); ins(a[i].y,a[i].x); } if(n&1){ puts("-1"); return 0; } dfs(1,-1); int ans=0; for(int i=1;i<n;++i){ int x=a[i].x,y=a[i].y; if(dep[x]<dep[y]) swap(x,y); if(!(size[x]&1)) ans++; } printf("%d\n",ans); }
D - 字数统计 HDU - 1735
是个贪心题。一开始的思路错了,导致代码写的很复杂。初始化写错了,要不这题时能过的。。。
1.考虑最坏的情况,所有0都是被破坏的。 ans=0的个数。
2.段落的个数是固定的, ans=ans-2*段落个数。
3.考虑段尾,段位的0是不用算的,ans=ans-段尾0的个数。
4.我们要求ans的最小值,1和2都是固定的,也就是要求段尾0个数的最大值。
5.可能的段落数要大于题目给的段落数,取段尾0多的段落就行了。
另外,最后一行一定是段尾,不要漏算了。
一开始写的超复杂代码。。。

#include<cstdio> #include<cstring> #include<queue> using namespace std; int a[10010][105],father[100010],num,num2; struct node{ int pre,suf,cnt; }pgh[10010],p[10010]; struct data{ int sum,x,y; bool operator < (const data &j) const { return sum>j.sum; } }; priority_queue<data> q; int find(int x){ if(x!=father[x]) father[x]=find(father[x]); return father[x]; } int main(){ int n,l,m; while(~scanf("%d%d%d",&n,&l,&m)){ while(!q.empty()) q.pop(); num=0; for(int i=0;i<=10010;++i){ pgh[i].pre=pgh[i].suf=pgh[i].cnt=0; p[i].pre=p[i].suf=p[i].cnt=0; } for(int i=1;i<=n;++i) for(int j=1;j<=l;++j) scanf("%d",&a[i][j]); int i=1; while(i<=n){ if(a[i][1]==0&&a[i][2]==0){ int tmp=0; for(int j=l;j>=1;--j) if(a[i-1][j]==0) tmp++; else break; pgh[num].suf=tmp; tmp=0; for(int j=1;j<=l;++j) if(a[i][j]==0) tmp++; else break; pgh[++num].pre=tmp; } for(int j=1;j<=l;++j) if(a[i][j]==0) pgh[num].cnt++; i++; } for(int i=1;i<=num;++i) father[i]=i; for(int i=1;i<num;++i){ q.push((data){pgh[i].suf,i,i+1}); } for(int i=1;i<=num-m;++i){ data tmp; tmp=q.top(); q.pop(); int x=tmp.x,y=tmp.y; int r1=find(x),r2=find(y); father[r2]=r1; } int root=find(1); num2=1; p[num2].pre=pgh[1].pre; for(int i=1;i<=num;++i){ if(find(i)==root) p[num2].cnt+=pgh[i].cnt; else{ root=find(i); p[num2].suf=pgh[i-1].suf; p[++num2].pre=pgh[i].pre; p[num2].cnt=pgh[i].cnt; } } p[num2].suf=0; for(int j=l;j>=1;--j) if(a[n][j]==0) p[num2].suf++; else break; int ans=0; for(int i=1;i<=num2;++i) ans=ans+p[i].cnt-2-p[i].suf; printf("%d\n",ans); } return 0; }
想的是把多段落合并,其实合并的操作并不需要写出来,只需要段尾0的个数就行了。
而且段首的0的个数并没有什么用,是我想错了。。。如果段首有用的话大概我这样写就对了。
简单的
https://blog.csdn.net/snowy_smile/article/details/49666233

#include<cstdio> #include<cstring> #include<algorithm> using namespace std; int n,m,p; int a[105],b[10010]; int main(){ while(~scanf("%d%d%d",&n,&m,&p)){ int ans=0,num=0,ed=0; for(int i=1;i<=n;++i){ for(int j=1;j<=m;++j){ scanf("%d",&a[j]); ans+=a[j]==0; } if(a[1]==0&&a[2]==0) b[++ed]=num; for(int j=m;j>=1;--j) if(a[j]==1){ num=m-j; break; } } ans=ans-2*p-num; sort(b+1,b+ed+1); for(int i=ed;i>=ed-p+2;--i) ans-=b[i]; printf("%d\n",ans); } return 0; }
....................................
F - Semifinals CodeForces - 378B
题目大意:有两场半决赛,每场各有n各人参加,现在有一个k值,表示说半决赛的前k名可以直接晋级总决赛,因为要选出n个人参加决赛,所以2*(n -k)要在剩下的人中选前2*(n-k)名,k的取值范围为0~n/2,问说那些人是有可能晋级决赛的。
解题思路:直接按照k = 0和k = n / 2的方案去选,就包括了所有可以晋级的人选,两种极端。
————————————————
原文链接:https://blog.csdn.net/keshuai19940722/article/details/18864545
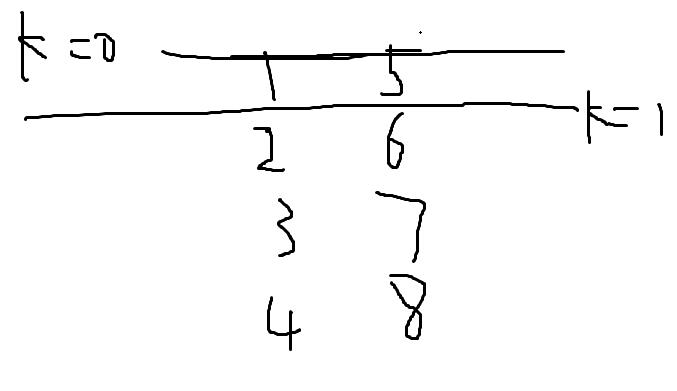
对于上图 1,5,2,6是能入选的。 现在考虑3能不能入选。
首先3要是能入选1.2肯定也能。
1. k=0时,3要想入选至少要比6小。
2. k=1时,1和5入选,
i,3比5大,不影响结果
ii,3比5小,也就是说一个比3劣的元素入选了,结果肯定不如k=0时;
综上可得,k=0时的解至少不会比k=1时的差,所以直接考虑k=0时,和k=n/2时就行了。

#include <stdio.h> #include <string.h> const int N = 100005; int n, a[N], b[N]; int main() { scanf("%d", &n); for (int i = 0; i < n; i++) scanf("%d%d", &a[i], &b[i]); int p = 0, q = 0, k = n / 2; for (int i = 0; i < n; i++) { if (a[p] < b[q]) p++; else q++; } for (int i = 0; i < n; i++) { if (i < p || i < k) printf("1"); else printf("0"); } printf("\n"); for (int i = 0; i < n; i++) { if (i < q || i < k) printf("1"); else printf("0"); } printf("\n"); return 0; } ———————————————— 版权声明:本文为CSDN博主「JeraKrs」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。 原文链接:https://blog.csdn.net/keshuai19940722/article/details/18864545
我的思路:如果3想入选至少要比6小,如果4想入选至少要比5小。

#include<cstdio> #include<cstring> using namespace std; const int N=1000010; int n,a[N],b[N],ansa[N],ansb[N]; int main(){ scanf("%d",&n); for(int i=1;i<=n;++i) scanf("%d%d",&a[i],&b[i]); int t=n/2; for(int i=t+1;i<=n;++i){ int j=n-i+1; if(a[i]<b[j]) ansa[i]=1; } for(int i=t+1;i<=n;++i){ int j=n-i+1; if(b[i]<a[j]) ansb[i]=1; } for(int i=1;i<=t;++i) ansa[i]=ansb[i]=1; for(int i=1;i<=n;++i) printf("%d",ansa[i]); printf("\n"); for(int i=1;i<=n;++i) printf("%d",ansb[i]); return 0; }
I - Pie or die CodeForces - 55C
第一次接触博弈论的题,差一点啊,我试到了4,结果答案是5,我太难了!应该多在纸上画一画。
【题意】 有一个n*m的棋盘,上面有k个棋子,先手每次可以移动一个棋子去相邻的格子,如果能够把某个棋子移动到棋盘外面,则先手获胜;后手每次可以封闭一个边界(两个顶点之间的边,封闭后不能从该边移动到边界外面),如果先手不能够把某个棋子移动到棋盘外面,则后手胜;
【思路】分析棋盘可以发现,对于四个角落来说,每个角落都有两条边,也就是说四个角落一共多出四条边,加上原先边界的一条边,则一共5条边,所有当某个棋子距离边界的距离小于5的时候,这五条边一定存在某条边没有被封闭,则先手必胜,否则先手必败。
————————————————
原文链接:https://blog.csdn.net/i1020/article/details/79791234

#include<cstdio> #include<cstring> using namespace std; int n,m,k,p[106][3]; int main(){ scanf("%d%d%d",&n,&m,&k); for(int i=1;i<=k;++i){ scanf("%d%d",&p[i][0],&p[i][1]); } bool flag=0; for(int i=1;i<=k;++i){ int x=p[i][0],y=p[i][1]; if(x<=5||x>=n-4) flag=1; if(y<=5||y>=m-4) flag=1; if(flag) break; } if(flag) puts("YES"); else puts("NO"); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号