质数判定方法
原文地址:https://www.luogu.org/blog/zyb2624936151/shuo-lun-zhi-shuo-ji-ji-shai-fa
update on 2018/12/01 12:51
最前边的一些话
-
如果你连素数都不知道是什么,我建议你可以试试滚学科了
-
如果你可以秒切这道题,那么这篇文章也帮不了你这个dalao,你也可以
滚去看别的文章了 -
这篇文章的源码基本有10k,LZ在后边敲的时候都一卡一卡的,希望能耐心看下去,
另外来骗个赞
0:一些前言
在 $OI$ 中,素数自古以来就是常考点,在 $NOIP$ 等竞赛中,也多次涉及到关于素数的知识点,对于一个 $OIerDb$ 来说,应对这些考试最好的方法就是如何快速判断一个数是不是素数和打出一个大范围的质数表。
接下来,我们将要学习这些方法。
另:lz不太会用 $\LaTeX$ ,凑合看吧
1:如何判断一个数是不是质数。
- 1:根据定义:素数就是一个数除了 $1$ 和他本身没有其他因数的数叫做质数。
于是我们对于一个 $N$ ,可以可以从 $2$ 枚举到 $N-1$ ,从而判断这个数是不是质数。
代码如下:
bool Is_prime(int n);
{
if(n==1)return false;
if(n==2)return true;
for(register int i=2;i<n;i++)
if(n%i==0)return false;
return true;
}时间复杂度为 $O(N)$ 。
对于上述程序显然不能满足我们的需求,如 $N$ 较大时,这样的程序肯定会超时,我已我们要想办法优化以上程序。
优化一
我们不难发现 $N$ 的因数是成对出现的,所以对于任何一个整数 $N$ ,我们只需要从 $1$ 枚举到 $\sqrt{N}$ 就可以了。
于是代码如下:
bool Is_prime(int n);
{
if(n==1)return false;
if(n==2)return true;
for(register int i=2;i*i<=n;i++)
if(n%i==0)return false;
return true;
}上述程序时间复杂度为 $O(\sqrt{N})$
优化2
根据lz多年的经验,已经达到 $O(\sqrt{N})$ 的算法验证是不是素数的算法已经是最快的算法,知道有一天看到了这篇文章
证明:令 $x≥1$ ,将大于等于 $5$ 的自然数表示如下: $......6x-1,6x,6x+1,6x+2,6x+3,6x+4,6x+5,6(x+1),6(x+1)+1......$
可以看到,不在6的倍数两侧,即 $6x$ 两侧的数为 $6x+2,6x+3,6x+4...$ 由于 $2(3x+1),3(2x+1),2(3x+2),$
所以它们一定不是素数,再除去 $6x$ 本身,显然,素数要出现只可能出现在 $6x$ 的相邻两侧。
所以,基于以上条件,我们假如要判定的数为 $n$ ,则 $n$ 必定是 $6x-1$ 或 $6x+1$ 的形式,对于循环中 $6i-1$ , $6i$ , $6i+1$ , $6i+2,6i+3,6i+4$ ,其中如果 $n$ 能被 $6i$ , $6i+2$ , $6i+4$ 整除,则 $n$ 至少得是一个偶数,
但是 $6x-1$ 或 $6x+1$ 的形式明显是一个奇数,故不成立;另外,如果 $n$ 能被 $6i+3$ 整除,则n至少能被 $3$ 整除,
但是 $6x$ 能被 $3$ 整除,故 $6x-1$ 或 $6x+1$ (即 $n$ )不可能被 $3$ 整除,故不成立。综上,循环中只需要考虑 $6i-1$ 和 $6i+1$ 的情况,
即循环的步长可以定为 $6$ ,每次判断循环变量 $k$ 和 $k+2$ 的情况即可,代码如下:
bool Is_prime(int n)
{
if(n==1) return false;
if(n==2||n==3) return true;
if(n%6!=1&&n%6!=5) return false;
for(register int i=5;i*i<=n;i+=6)
if(n%i==0||n%(i+2)==0) return false;
return true;
}理论上讲整体速度应该会是优化1代码的三倍的3倍。即 $O(\frac{\sqrt{N}}{3})$
暂且就这么认为吧
小结:在对于素数的判断时,一般用第一种的优化方法就可以了,但是如果遇到了毒瘤出题人,最好是用第二种方法。
2:质数的筛法
0:使用第一种优化的方法从 $1$ 到 $N$ 判断每一个数是不是素数,时间复杂度为 $O(N\sqrt{N})$
代码:
bool Is_prime(int n);
{
if(n==1)return false;
if(n==2)return true;
for(register int i=2;i*i<=n;i++)
if(n%i==0)return false;
return true;
}
const int N=100010
bool prime[N];
void make_prime()
{
for(ri i=1;i<=N;i++)
prime[i]=Is_prime(i);
return;
}1:一般筛法(埃拉托斯特尼筛法):
基本思想:素数的倍数一定不是素数
实现方法:用一个长度为 $N+1$ 的数组保存信息( $true$ 表示素数, $false$ 表示非素数),先假设所有的数都是素数(初始化为 $true$ ),从第一个素数 $2$ 开始,把 $2$ 的倍数都标记为非素数(置为 $false$ ),一直到大于 $N$ ;然后进行下一趟,找到 $2$ 后面的下一个素数 $3$ ,进行同样的处理,直到最后,数组中依然为 $true$ 的数即为素数。
$P.S.:$ 特别的, $1$ 既不是素数,也不是合数,所以 $1$ 要置为 $false$
例如,我们要求 $1-100$ 之间的素数,整个过程是这样的。
我们先把 $2$ 标记上 $true$ ,然后把从 $2-100$ 中所有 $2$ 的倍数标为 $false$ 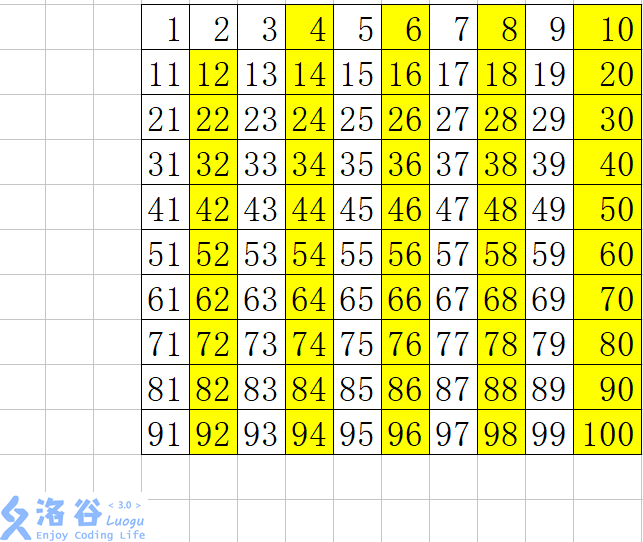
然后我们找到下一个素数 $3$ 标记为 $true$ ,把 $3$ 的倍数标为 $false$ 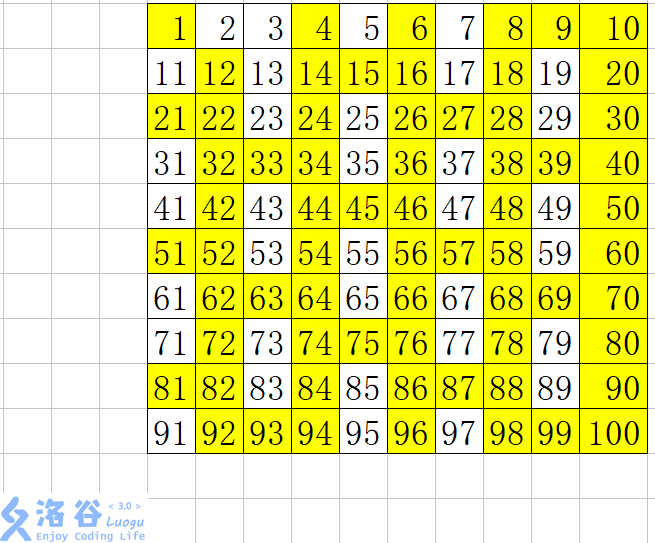
然后我们又找到了 $5$ ,把 $5$ 的倍数标为 $false$ 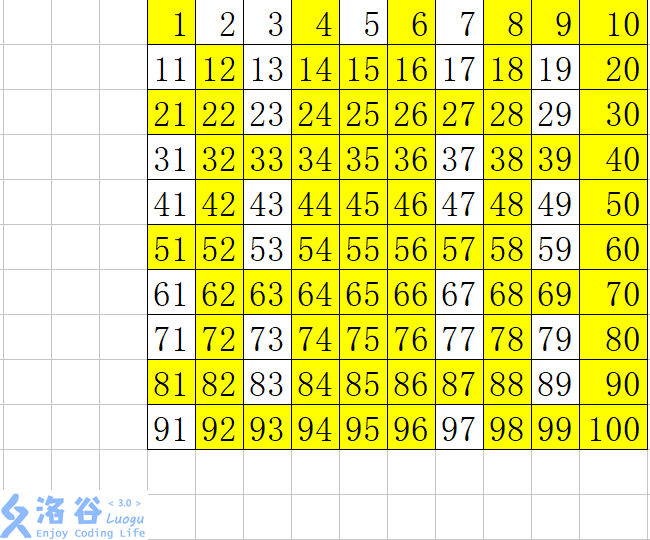
我们重复着上述过程,完成了对 $1-100$ 以内素数的检索。 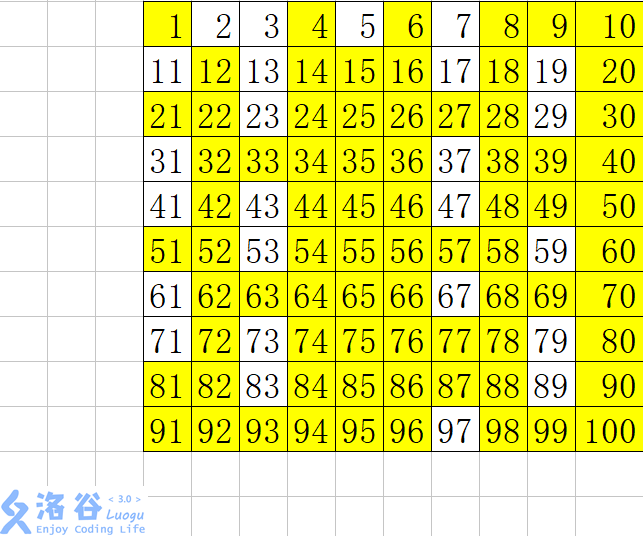
另附这里有一张动图,还不懂的同学可以参照这幅图理解 
代码如下:
#include<cstring>
#include<cmath>
const int MAXN=1000010;
bool prime[MAXN];
void make_prime)()
{
memset(prime,true,sizeof(prime));
prime[0]=prime[1]=false;
int t=sqrt(MAXN);
for(register int i=2;i<=t;i++)
{
if(prime[i])
{
for(register int j=2*i;j<MAXN,j+=i)
{
prime[j]=false;
}
}
}
return;
}此方法的复杂度为 $O(\sum_{p<n}\frac{n}{p})=O(nloglogn)$
通过上述代码,我们发现此方法还可以继续优化,因为上述的方法中,每一个有多组因数可能会被筛多次,例如: $30$ 会被 $2,3,5$ 各筛一次导致计算冗余,我们可以对此方法进行改进,得到更加高效的筛法(欧拉筛)
代码如下:
#include<cstring>
#incldue<cmath>
const int MAXN=1000010;
bool prime[MAXN];
int Prime[MAXN];
int num=0;
void make_prime()
{
memset(prime,true,sizeof(prime));
prime[0]=prime[1]=false;
for(int i=2;i<=MAXN;i++)
{
if(prime[i])
{
Prime[num++]=i;
}
for(int j=0;j<num&&i*Prime[j]<MAXN;j++)
{
prime[i*Prime[j]]=false;
if(!(i%Prime[j]))
break;
}
}
return;
}这个方法可以保证每个和合数在 $N/M$ 的最小素因子时被筛出,所以时间复杂度仅为 $O(N)$ 已经可以满足大部分需求,在竞赛中,这种方法也可以在极短的时间内求出关于 $N$ 的质数表。
但是这个算法的弊端在于,为了判断一个大数是否是素数必须从从头开始扫描,而且空间代价也受不了,故不能离散的判断。
所以,我们要引入更高效的算法——Miller_Rabin算法。
Miller_rabin算法描述
首先介绍一下 $miller$ $rabin$ 算法。
miller_rabin是一种素性测试算法,用来判断一个大数是否是一个质数。 miller_rabin是一种随机算法,它有一定概率出错,设测试次数为 $s$ ,那么出错的概率是 $4^{-s}$ ,至于为什么我也不会证明。我觉得它的复杂度是 $O(slog^2n)$ ,因为你要进行 $s$ 次,每次要进行一次快速幂,每次快速幂要 $O(log n)$ 次快速乘,每次快速乘又是 $log n$ 的,所以这一部分是 $log^{2} n$ 的,另一部分是把 $n$ 分解成 $u*2^{k}$ ,复杂度是 $log n$ ,所以 $k$ 是 $log n$ 量级的,对于 $k$ ,每次要快速乘,所以这一部分的复杂度也是 $log^{2}n$ 的,于是总复杂度 $O(mlog^{2}n)$
下面开始介绍miller_rabin的做法。
首先我们知道,根据费马小定理,如果 $p$ 为质数且 $a$ 与 $p$ 互质,那么有
$$a^{p-1}\equiv1\pmod{p}$$
如果我们让 $a<n$ ,那么只需要满足 $p$ 为质数即可。但是反过来,满足 $$a^{p-1}\equiv1\pmod{p}$$ 的 $p$ 不一定是质数。但是幸运的是,对于大多数的 $p$ ,费马小定理的逆定理是对的,但是为了让我们得到正确是结果,我们需要提高正确率。所以接下来我们需要二次探测。
若 $n$ 为质数,并且 $$x^{2}\equiv1\pmod{n}$$
那么 $x=1$ 或 $x=n-1$ ,因为 $x2=1$ ,则 $x=1$ 或 $x=-1$ ,而在模意义下这个 $-1$ 就成了 $n-1$ 。我们来证明一下为什么在 $x^{2}\equiv1\pmod{p}$ ,且 $x≠1(mod p)$ ,且 $x≠p-1(mod p)$ 时 $p$ 不是质数。
$$x^{2}\equiv1\pmod{p}$$
$$x^{2}-1\equiv0\pmod{p}$$
$$(x-1)(x+1)\equiv0\pmod{p}$$
所以有 $p|(x-1)p|(x-1)$ 或 $p|(x+1)p|(x+1)$ 或 $p|(x+1)(x-1) $
因为 $x≠p-1(mod$ $p)$
所以 $(x+1)mod$ $p≠0$ , $p$ 不整除 $x+1$
因为 $x≠1(mod$ $p)$
所以 $(x-1)$ $mod$ $p≠0$ ,pp不整除 $x-1$
所以只能是 $p|(x+1)(x-1)$
由此我们可以发现 $x+1$ 和 $x-1$ 都不含 $p$ 的所有因子,而它们的乘积却含有的 $p$ 的全套因子,那么在相乘时 $x+1$ 和 $x-1$ 分别提供了一个非 $1$ 非 $p$ 的因子,才能使乘积是 $p$ 的倍数,当然这两个因子可能相同。
那么,我们可以证明出 $p$ 可以表示为两个非 $1$ 非 $p$ 的数的乘积,那么就证明了 $p$ 是合数而不是质数了。
我们可以根据这个性质进行二次探测。
如果我们设要测试的数为 $n,$ 若 $n$ 是 $2$ 或 $n$ 是偶数,那么我们可以直接判断 $n$ 的奇偶,否则令 $p=n?1$ ,将 $p$ 分解成 $u*2^{k}$ ,枚举 $k$ 来不断进行二次探测。则那么我们随机一个底数 $x$ ,快速幂求出 $x^{u}$ $mod$ $n$ ,然后不断的 $x*x$ $mod$ $p$ 来进行二次探测。
至于为什么在代码中这么做是对的,我看到一个很好的解释,在这里分享一下。
$$a^{p-1}\equiv1\pmod{p}$$
$$a^{u*2{k}}\equiv1\pmod{p}$$
$$a^{u*2^{k-1}}*a^{u*2^{k-1}}\equiv1\pmod{p}$$
那么我们把 $a^{u*2^{k-1}}$ 看作 $x$ ,那么就是在当前 $a^{u*2^{k-1}}\equiv1\pmod{p}$ 的时候验证是否是 $p-1$ 或者 $1$ 即可。 另外最后别忘了用费马小定理来判断一下,代码中的 $x$ 其实的 $x^{p-1}\equiv1\pmod{p}$ 之后的结果,所以只需要看最后的 $x$ 是否是 $1$ 即可。
代码实现如下:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <map>
#define ll long long
using namespace std;
const int times = 20;
int number = 0;
map<ll, int>m;
ll Random(ll n)//生成[ 0 , n ]的随机数
{
return ((double)rand()/RAND_MAX*n+0.5);
}
ll q_mul(ll a, ll b, ll mod)//快速计算 (a*b) % mod
{
ll ans=0;
while(b)
{
if(b&1)
{
b--;
ans=(ans+a)%mod;
}
b/=2;
a=(a+a)%mod;
}
return ans;
}
ll q_pow(ll a,ll b,ll mod)//快速计算 (a^b) % mod
{
ll ans=1;
while(b)
{
if(b&1)
{
ans=q_mul(ans,a,mod );
}
b/=2;
a=q_mul(a,a,mod);
}
return ans;
}
bool witness(ll a,ll n)//miller_rabin算法的精华
{//用检验算子a来检验n是不是素数
ll tem=n-1;
int j=0;
while(tem%2==0)
{
tem/=2;
j++;
}
//将n-1拆分为a^r * s
ll x=q_pow(a,tem,n); //得到a^r mod n
if(x==1||x==n-1) return true;//余数为1则为素数
while(j--) //否则试验条件2看是否有满足的 j
{
x=q_mul(x,x,n);
if(x==n-1)return true;
}
return false;
}
bool miller_rabin(ll n)//检验n是否是素数
{
if(n==2)return true;
if(n<2||n%2==0)return false;//如果是2则是素数,如果<2或者是>2的偶数则不是素数
for(register int i=1;i<=times;i++)//做times次随机检验
{
ll a=Random(n-2)+1;//得到随机检验算子 a
if(!witness(a,n))return false;//用a检验n是否是素数
}
return true;
}
int main()
{
ll x;
while(cin>>x)
{
if(miller_rabin(x))
cout<<"Yes"<<endl;
else
cout <<"No"<<endl;
}
return 0;
}(话说这个应该归到判断素数的里边啊算了不搬了)
另附:某位大佬在 $PPT$ 上的一个神仙算法
此算法是 $O(n^{\frac{3}{4}}/log n)$ 的,并且在该算法在洲阁筛和min25筛中应用广泛(作为一部分)
这个算法名字好像叫做 $$the Meissel, Lehmer, Lagarias, Miller, Odlyzko method$$ ,网上的资料比较少。
首先放几个定义,定义比较多。。。
$P_i$ 表示第 $i$ 个素数,
$PI_i$ 表示 $i$ 以内素数个数,
$F_{n,m}$ 表示 $n$ 以内不等于第 $i$ 至 $m$ 个素数及其倍数的数的个数,
$P2_{n,m}$ 表示 $n$ 以内只有两个素因数且最小的素因数大于 $P_m$ 的数的个数,
$P3_{n,m}$ 表示 $n$ 以内只有三个素因数且最小的素因数大于 $P_m$ 的数的个数。
- 注意,接下来提到的除法都是指向下取整。
f明显可以递归计算,转移方程: $f[n,m] = f[n,m-1] + f[n/p[m],m-1]$
根据大佬的 $PPT$ ,计算f的时间复杂度是 $O(m*n^{\frac{1}{2}})$ 。 但是蒟蒻我根本不会证明。。
然后是 $p2$ 的计算方法。 $p2[n,m] = \sum_{P_i[n/k]} - pi[k] + 1$ ,其中 $k$ 是所有大于 $P_m$ 且小于 $n^{\frac{1}{2}}$ 的素数。
接着是p3的计算方法。 $p3[n,m] = \sum_{p2[n/k,pi[k]-1]}$ ,其中 $k$ 是所有大于 $P_m$ 且小于 $n^{\frac{1}{3}}$ 的素数。
先介绍第一种计算 $Pi_n$ 的方法。线性筛预处理前 $n^\frac{1}{2}$ 的 $p$ 和 $Pi$ 。
pi $[n]=pi[n^{\frac{1}{3}}]+f[n,pi[n^{\frac{1}{3}}]]-1-p2[n,pi[n^{\frac{1}{3}}]]$ 。减一是为了排除掉1。
这种方法的时间复杂度是 $O(n^{\frac{5}{6}} / log(n))$ 。时间复杂度的瓶颈在f的计算上,其中 $pi[n^{\frac{1}{3}}] ≈ n^{\frac{1}{3}} / log n$ 。
为了进一步改善时间复杂度,我们要尽量减少 $f$ 的计算。以下是经过改进的第二种方法。
还是线性筛预处理前 $n^{\frac{1}{2}}$ 的 $p$ 和 $pi$ 。
得到:
$$pi[n] = pi[n^{\frac{1}{4}}] + f[n,pi[n^{\frac{1}{4}}]] - 1 - p2[n,pi[n^{\frac{1}{4}}]] - p3[n,pi[n^{\frac{1}{4}}]]$$
计算 $p3$ 的时间复杂度还不到 $O(n^{\frac{2}{3}})$ ,所以瓶颈还在 $f$ 上,总时间复杂度为 $O(n^{\frac{3}{4}} / log n)$ 。
代码看看就好了。。。。
#include<cstdio>
#include<iostream>gt;
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<ctime>
#pragma warning(disable:4996)
#define INF 2000000005
#define lowbit(a) ((a)&-(a))
#define FAIL -INF
const long long MAXN=6893911;
long long p[MAXN], cnt;
bool mark[MAXN];
int pi[MAXN];
void init()
{
long long i,j;
for (i=2;i<MAXN;i++)
{
if (!mark[i])
p[cnt++]=i;
pi[i]=pi[i-1]+!mark[i];
for (j=0;p[j]*i<MAXN&&j<cnt;j++)
{
mark[p[j]*i]=true;
if (i%p[j]==0)
break;
}
}
}
int f(long long n,int m)
{
if (n==0)return 0;
if (m==0)return n-n/2;
return f(n,m-1)-f(n/p[m],m-1);
}
int Pi(long long N);
int p2(long long n, int m)
{
int ans=0;
for (int i=m+1;(long long)p[i]*p[i]<=n;i++)
ans+=Pi(n/p[i])-Pi(p[i])+1;
return ans;
}
int p3(long long n, int m)
{
int ans=0;
for (int i=m+1;(long long)p[i]*p[i]*p[i]<=n;i++)
ans+=p2(n/p[i],i-1);
return ans;
}
int Pi(long long N)
{
if (N<MAXN)return pi[N];
int lim=f(N,0.25)+1;
int i;
for (i=0;p[i]<=lim;i++);
int ans=i+f(N,i-1)-1-p2(N,i-1)-p3(N,i-1);
return ans;
}
int main()
{
long long L,R;
scanf("%lld %lld",&L,&R);
init();
printf("%d",Pi(R)-Pi(L-1));
return 0;
}例题:
可自己练习话说题目很基础啊

