Java数据结构和算法(八)--红黑树与2-3树
红黑树规则:
1、每个节点要么是红色,要么是黑色
2、根节点都是黑色节点
3、每个叶节点是黑色节点
3、每个红色节点的两个子节点都是黑色节点,反之,不做要求,换句话说就是不能有连续两个红色节点
4、从任意节点到所有叶子节点上的黑色节点数量是相同的
一般对红黑树的讲述都是先给出这样的定义,这样想对不太容易理解的,而在算法4一书中,直接跳过这些规则,而讲述了红黑树与2-3树的等价性。如果我们先了解2-3树,理解了红黑树与2-3树之间的关系,再来看这些规则,就容易理解了
2-3树:
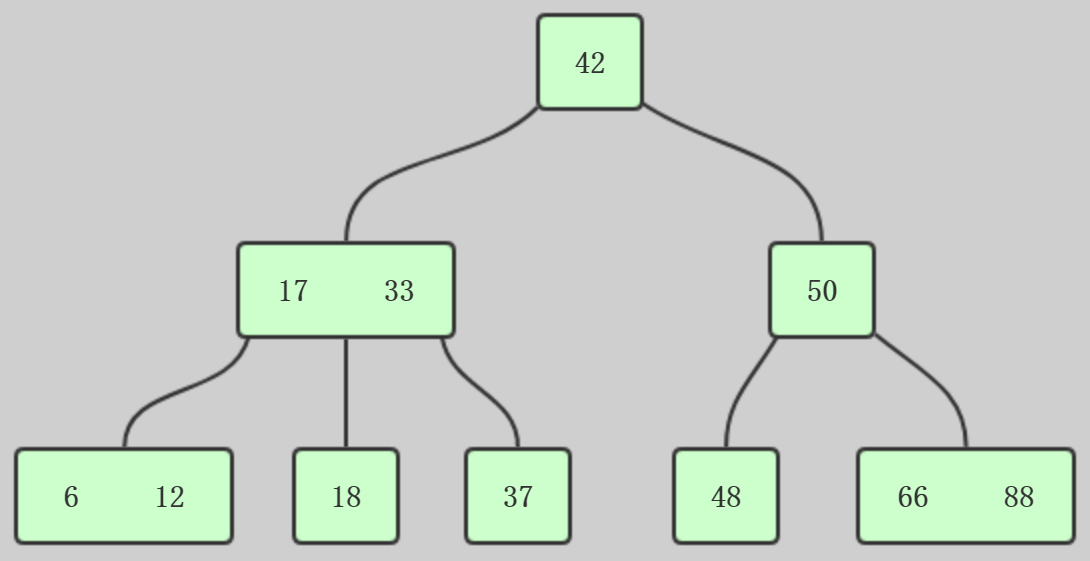
2-3树满足二分搜索树的基本性质,但是不是二叉树
2-3树节点可以存放一个元素或两个元素,每个节点有两个(2节点)或三个子节点(3节点),这就是2-3树
2-3树是一个绝对平衡的树
2-3树的绝对平衡性:
1、2-3树新插入的节点一定不能插到空节点的位置
2、如果一个新节点插入到2节点,就会形成3节点

3、如果一个新节点插入到3节点,临时形成4节点,然后进行变形
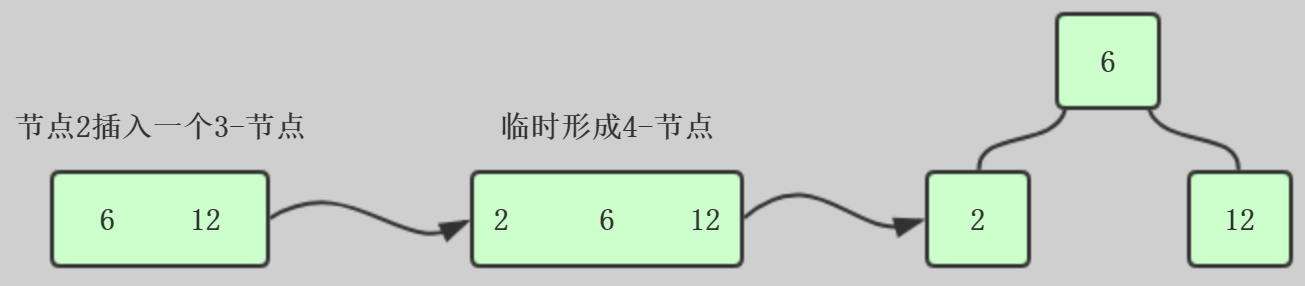
如果这个节点是根节点,这样就处理完了,如果插入的节点是叶子节点
1).父节点为2-节点

2).父节点为3-节点

通过上面的规则,实现了2-3树的绝对平衡
红黑树和2-3树的等价性:
将2节点与3节点类比到红黑树
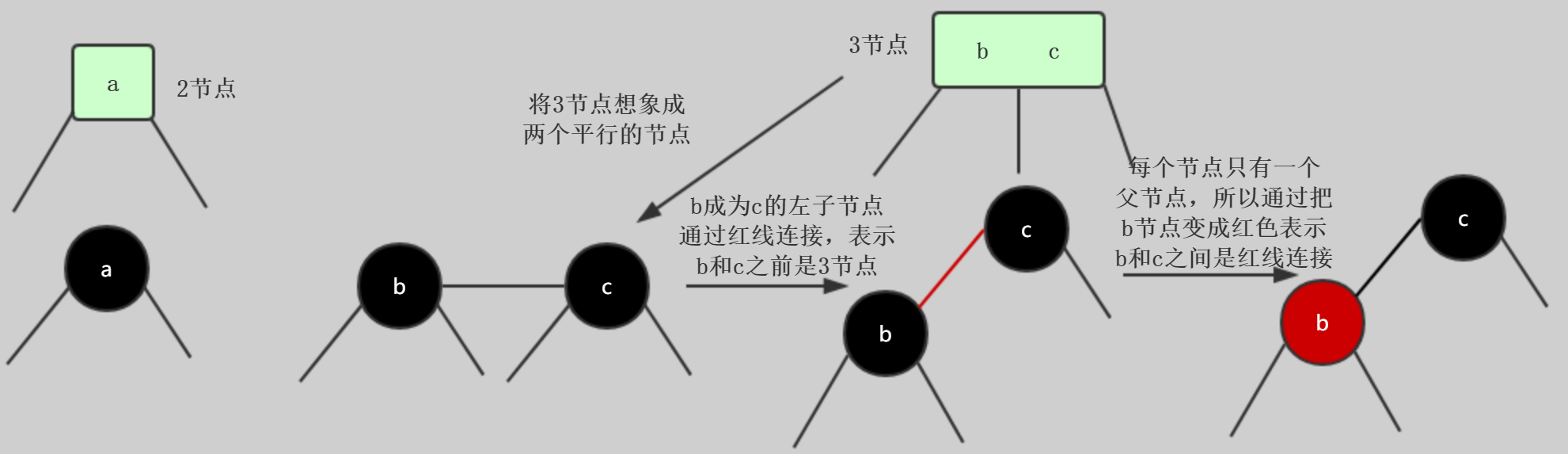
通过上面的过程,我们得到红黑树,所有红色节点都是左倾斜
实践:
所以此时我们很容易就能把2-3树转换为红黑树
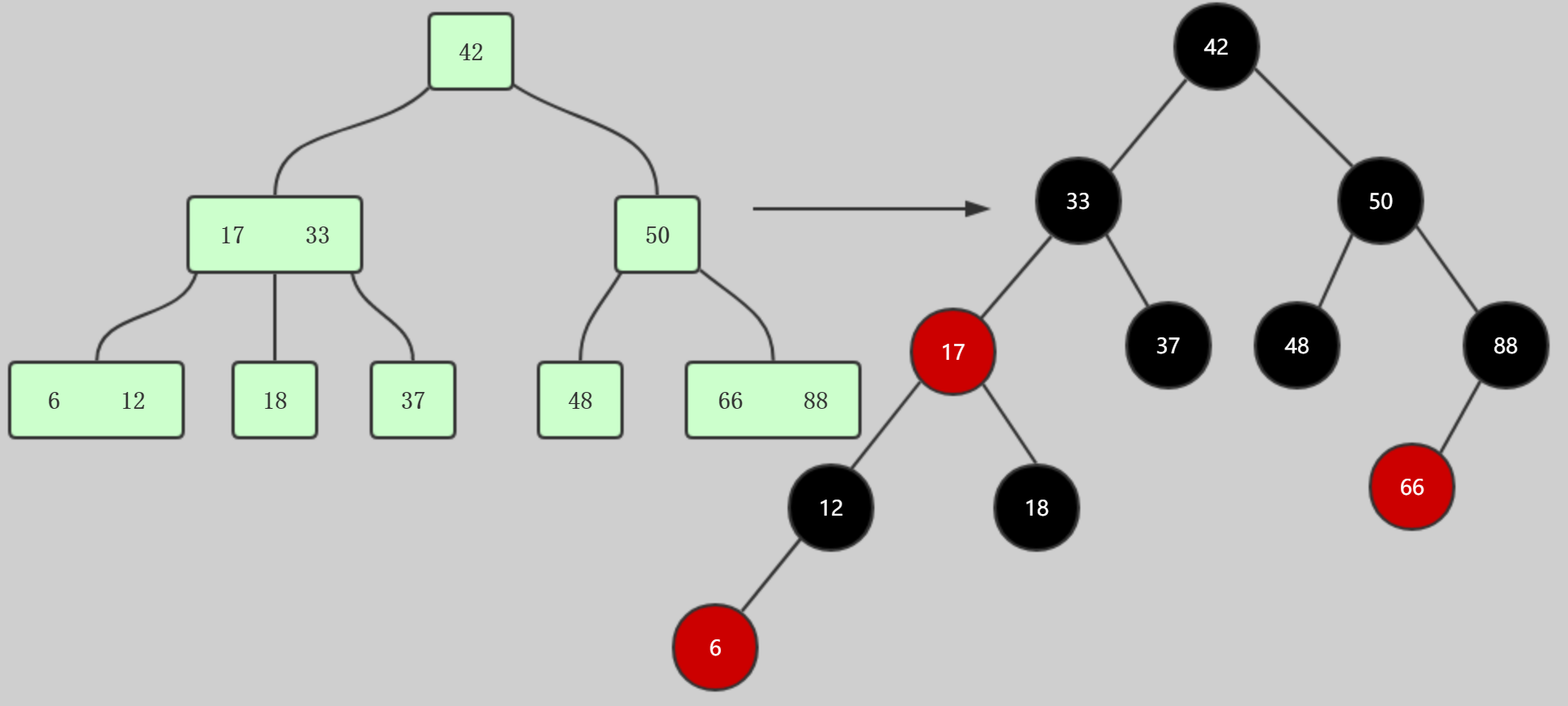
原来的2-3树有三个3-节点,所以红黑树中就有三个红色节点
通过2-3树理解红黑树的几个特征
特征:
1、每个节点要么是红色,要么是黑色
2、根节点是黑色节点
根节点肯定是黑色的,因为在2-3树中,根节点要么是2节点,要么是3节点,对应红黑树根节点肯定是黑色的
3、每个叶子节点(最后的空节点,而不是左右子树都为空的节点)是黑色节点
这里叶子节点是指这个节点为空,不是左右子树都为空的节点,包含空树的情况
if(node == null) return BLACK;
4、每个红色节点的两个子节点都是黑色节点,反之,不做要求,换句话说就是不能有连续两个红色节点
红色节点对应2-3树中的3节点,红节点的两个子节点对应3节点的左子节点和中间节点,这两个节点无论是2节点还是3节点,首先连接的肯定是黑色的,例如这里的17节点
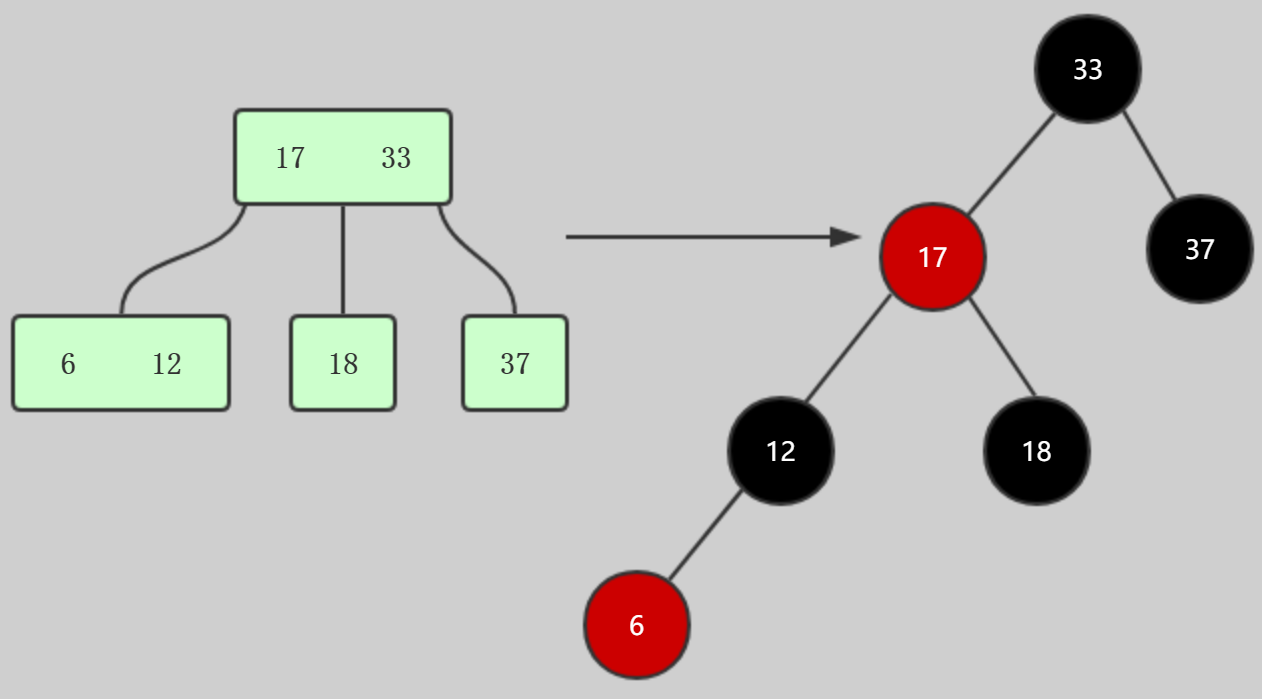
这里也可以看出来,黑色节点的右子节点肯定是黑色的,这个算是延伸内容
5、从任意节点到所有叶子节点上的黑色节点数量是相同的
这里类比到2-3树中,任意一个节点到叶子节点的经过的节点都是相同的,因为2-3是绝对平衡的树
从2-3树类比过来,任意一个节点到叶子节点经过的节点,无论是2节点还是3节点,肯定包含一个黑色的节点,但是红色不一定的,所以才有了第五条规则/特性
我们解释完了这五条特性,通过2-3树去理解,相比直接去死记硬背,简单很多
PS:红黑树是保持"黑色平衡"的二叉树,严格来说,不是平衡二叉树,最大高度:2logn,O(logn)
如果只是查询,AVL树的效率更高,如果删除和修改,红黑树更适合
Node定义:新添加节点默认红色
public class RBTree<K extends Comparable<K>, V> {
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node {
public K key;
public V value;
public Node left, right;
public boolean color;
public Node(K key, V value) {
this.key = key;
this.value = value;
left = null;
right = null;
//这里默认添加节点为红色,因为在2-3树新增加一个节点总是要和叶子节点融合的,这里不论后序操作,
//对应红黑树中一个红色节点和黑色节点
color = RED;
}
}
}
左旋:
// node x
// / \ 左旋转 / \
// T1 x ---------> node T3
// / \ / \
// T2 T3 T1 T2
private Node leftRotate(Node node){
Node x = node.right;
// 左旋转
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
return x;
}
红黑树的左旋和前面讲的AVL树左旋是相同的,只是有关于颜色的变化,想象2-3树添加场景,一个新节点添加到2节点,变成3节点
PS:这里不维护颜色的正确,只是左旋,颜色的维护在add()
颜色反转:往3节点添加一个更大的值,66添加到37-42
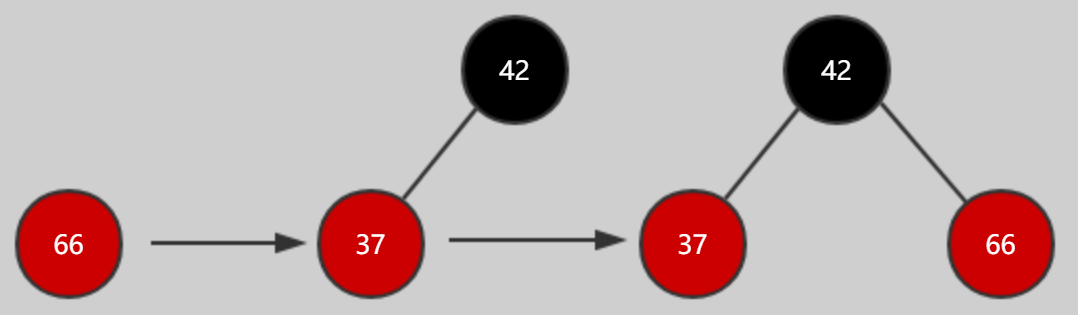
现在把节点66添加进来,对于二叉搜索树来说,会形成上面的结构
这样对于2-3树的场景:往3节点添加元素
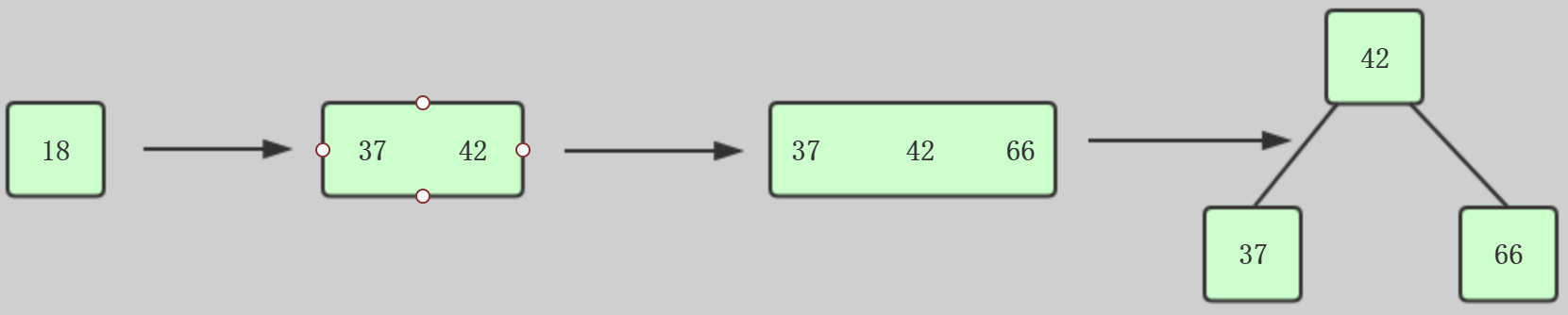
这时候,节点42需要向上融合,所以42应该是红色的,所以需要把节点42设置为红色
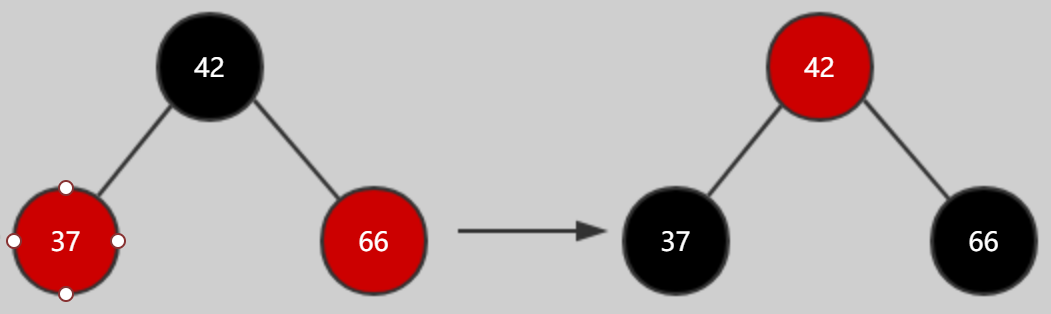
而红黑树的规则是:节点为红色,其两个子节点肯定是黑色的,所以有了上面的转变,也叫做颜色翻转,flipColors
//颜色翻转
private Node flipColors(Node node) {
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
return node;
}
右旋:往3节点添加一个更小的值,26添加到37-42
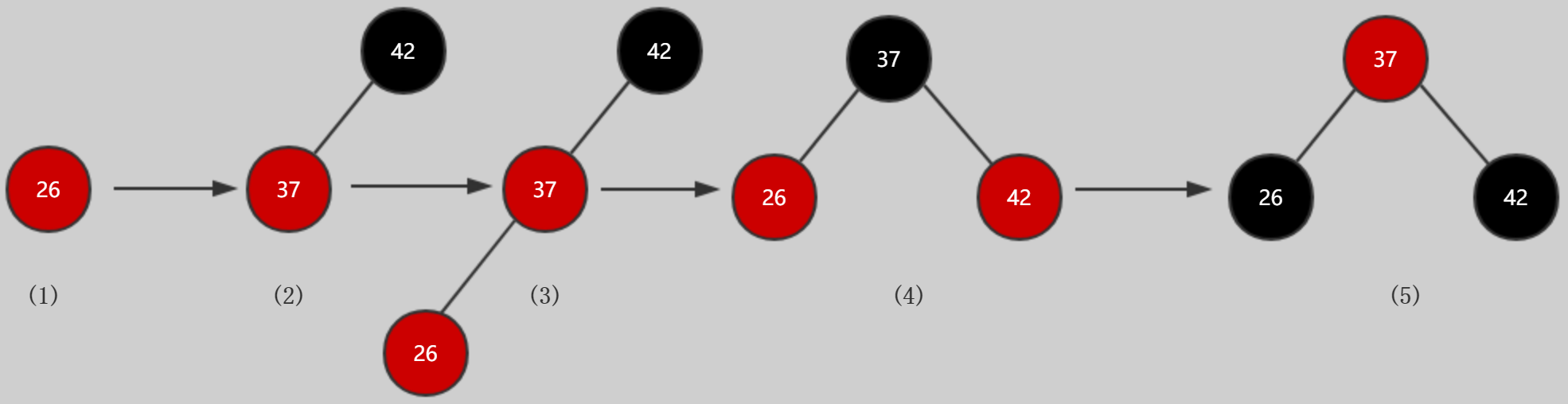
这种情况,自行对比2-3树场景,从(3)右旋,37的颜色要等于之前42的颜色为黑色,为了表示他们三个之前是一个4节点,所以42节点要变成
红色,右旋结束,然后进行颜色反转
// node x
// / \ 右旋转 / \
// x T2 -------> y node
// / \ / \
// y T1 T1 T2
private Node rightRotate(Node node){
Node x = node.left;
// 右旋转
node.left = x.right;
x.right = node;
x.color = node.color;
node.color = RED; //因为这种情况相当于形成4节点,所以需要设置为红色
return x;
}
我们上面讲述了左旋、右旋、颜色反转,分别对应着2-3树中:2节点添加、3节点添加更大的数据,3节点添加更小的值
如果往3节点添加一个中间值:例如40添加到37-42
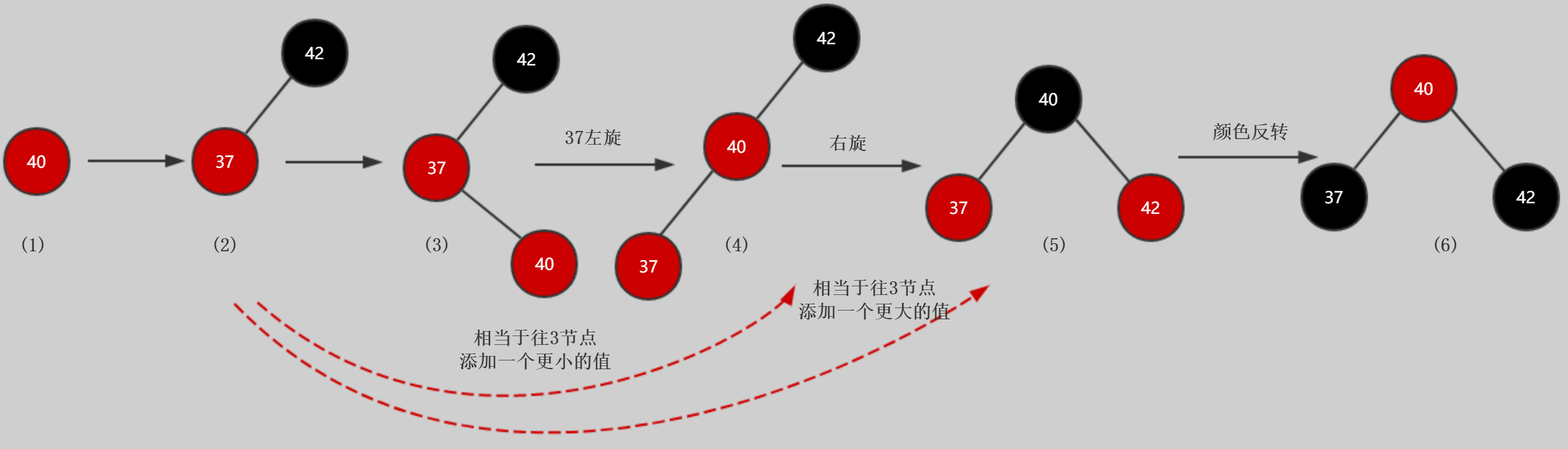
这种情况相当于:左旋+右旋+颜色反转,是最复杂的添加场景
可以包含上面讲的所有场景了,参考虚线描述,只是省略部分步骤,同样适用添加到2节点
红黑树添加元素:
// 向以node为根的红黑树中插入元素(key, value),递归算法
// 返回插入新节点后红黑树的根
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value); // 默认插入红色节点
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
if (isRed(node.right) && !isRed(node.left)) //右子节点为红色,左子节点为黑色
node = leftRotate(node);
if (isRed(node.left) && isRed(node.left.left)) //左子节点为红色,左子节点的左子节点为红色
node = rightRotate(node);
if (isRed(node.left) && isRed(node.right)) //左右子节点都是红色,惊醒颜色反转
flipColors(node);
return node;
}
左旋、右旋、颜色反转,这个顺序对应着上面的图
完整的RBTree.java代码:
public class RBTree<K extends Comparable<K>, V> {
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node{
public K key;
public V value;
public Node left, right;
public boolean color;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
color = RED;
}
}
private Node root;
private int size;
public RBTree(){
root = null;
size = 0;
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
// 判断节点node的颜色
private boolean isRed(Node node){
if(node == null)
return BLACK;
return node.color;
}
// node x
// / \ 左旋转 / \
// T1 x ---------> node T3
// / \ / \
// T2 T3 T1 T2
private Node leftRotate(Node node){
Node x = node.right;
// 左旋转
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
return x;
}
// node x
// / \ 右旋转 / \
// x T2 -------> y node
// / \ / \
// y T1 T1 T2
private Node rightRotate(Node node){
Node x = node.left;
// 右旋转
node.left = x.right;
x.right = node;
x.color = node.color;
node.color = RED;
return x;
}
// 颜色翻转
private void flipColors(Node node){
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}
// 向红黑树中添加新的元素(key, value)
public void add(K key, V value){
root = add(root, key, value);
root.color = BLACK; // 最终根节点为黑色节点
}
// 向以node为根的红黑树中插入元素(key, value),递归算法
// 返回插入新节点后红黑树的根
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value); // 默认插入红色节点
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
if (isRed(node.right) && !isRed(node.left))
node = leftRotate(node);
if (isRed(node.left) && isRed(node.left.left))
node = rightRotate(node);
if (isRed(node.left) && isRed(node.right))
flipColors(node);
return node;
}
// 返回以node为根节点的二分搜索树中,key所在的节点
private Node getNode(Node node, K key){
if(node == null)
return null;
if(key.equals(node.key))
return node;
else if(key.compareTo(node.key) < 0)
return getNode(node.left, key);
else // if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
public boolean contains(K key){
return getNode(root, key) != null;
}
public V get(K key){
Node node = getNode(root, key);
return node == null ? null : node.value;
}
public void set(K key, V newValue){
Node node = getNode(root, key);
if(node == null)
throw new IllegalArgumentException(key + " doesn't exist!");
node.value = newValue;
}
// 返回以node为根的二分搜索树的最小值所在的节点
private Node minimum(Node node){
if(node.left == null)
return node;
return minimum(node.left);
}
}
红黑树、AVL树、二分搜索树对比:
一共有三个测试:测试二分搜索树、 AVL树、红黑树的效率
Main.java:具体代码在上面GitHub地址
把英文版傲慢与偏见写入list,测试
for (String word : words) {
if (bst.contains(word))
bst.set(word, bst.get(word) + 1);
else
bst.add(word, 1);
}
for(String word: words)
bst.contains(word);
输出结果: BST: 0.130161098 s AVL: 0.124234987 s rbTree: 0.11852221 s BST: 0.137865554 s AVL: 0.120124769 s rbTree: 0.13707878 s BST: 0.143397424 s AVL: 0.153158411 s rbTree: 0.146772639 s
测试代码运行三次,我们看到三者差距并不大
1、在数据量不大的情况下,并不是时间复杂度更低的数据结构,效率一定更高
2、set()、contains()、get()几乎都是查询,红黑树的优势在于添加和查询
Main2.java:
int n = 20000000; Random random = new Random(n); ArrayList<Integer> testData = new ArrayList<>(n); for(int i = 0 ; i < n ; i ++) testData.add(random.nextInt(Integer.MAX_VALUE)); BST<Integer, Integer> bst = new BST<>(); for (Integer x: testData) bst.add(x, null);
生成两千万个随机数,添加到list,然后分别添加到二分搜索树、AVL树、红黑树
输出结果: BST: 53.912429302 s AVL: 52.037609212 s RBTree: 50.485452955 s
这里可以看到RBTree想对来说添加效率想对更高一点,但是由于测试时间太长,就测试一次,可能准确性可能不够,大家可以自行测试一下
Main3.java:
int n = 20000000; ArrayList<Integer> testData = new ArrayList<>(n); for(int i = 0 ; i < n ; i ++) testData.add(i);
这里和第二个测试区别就是添加有序数据,我们知道二分搜索树对于有序、倒序插入,就会退化为链表,所以这里只测试AVL树和红黑树
输出结果: AVL: 8.990460311 s RBTree: 6.297460938 s AVL: 8.462381117 s RBTree: 8.074237092 s AVL: 10.381852688 s RBTree: 6.812257725 s
总结:
1、对于随机数据,二分搜索树很好用,但是有序数据,会退化成链表,处于高度不平衡状态
2、AVL树是完全平衡的,适合查询的场景,例如get()、set()、contains()
3、红黑树不是平衡二叉树,统计性能更优(综合CURD操作),适合add()、del()


