Java数据结构和算法(七)--AVL树

在上篇博客中，学习了二分搜索树：Java数据结构和算法(六)--二叉树，但是二分搜索树本身存在一个问题：

如果现在插入的数据为1，2，3，4，5，6，这样有序的数据，或者是逆序。

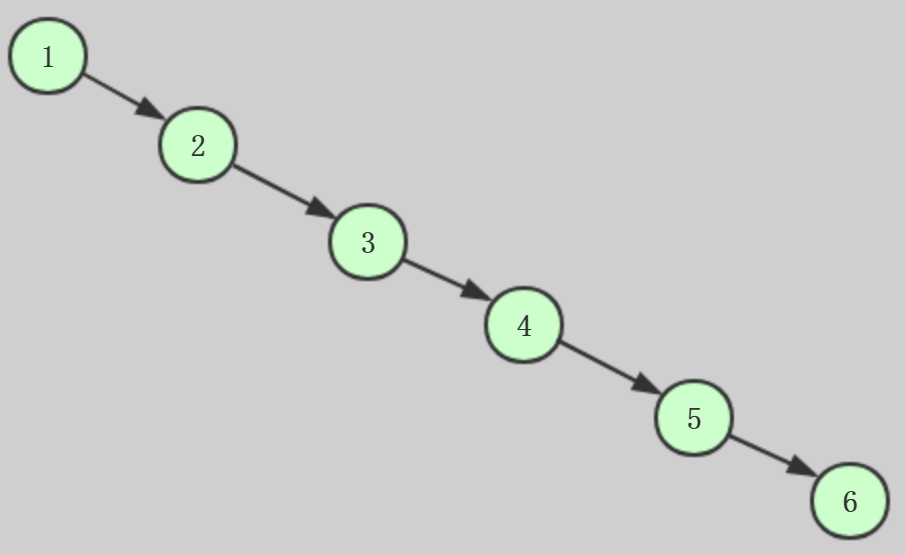
这种情况下的二分搜索树和链表几乎完全一样，是最不平衡的二叉树了，二分搜索树的效率直接降到最低。

如何解决上述问题：

使二分搜索树保持平衡二叉树的特征，而今天要讲述的AVL树是最经典的平衡二叉树了。

满二叉树：

　　除了叶子节点其余节点都有左右两个子节点的树。

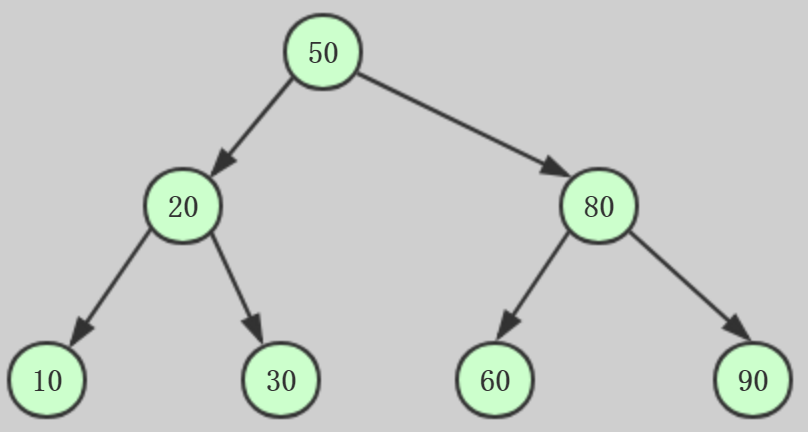
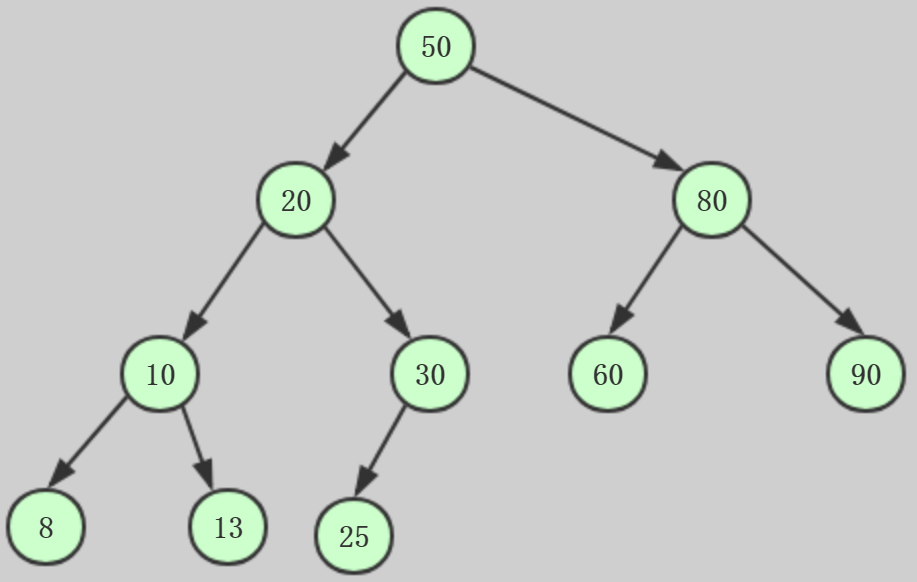
完全二叉树：

　　对于一个树高为h的二叉树，如果其第0层至第h-1层的节点都满。如果最下面一层节点不满，则所有的节点在左边的连续排列，空位都在右边。

简单总结：从上到下，从左到右的排列。这样的二叉树就是一棵完全二叉树。

 

AVL树：

AVL的名称来自其发明者G.M.Adelson-velsky 和E.M.Landis的首字母，是1962年提出的概念，平衡二叉搜索树也就是AVL树。

特征：

　　1、对于任意一个节点，左子树和右子树的高度差不能超过1。

　　2、平衡二叉树的高度和节点数量之间的关系也是O(logn)。

例如：现在在二分搜索树添加一个元素6。

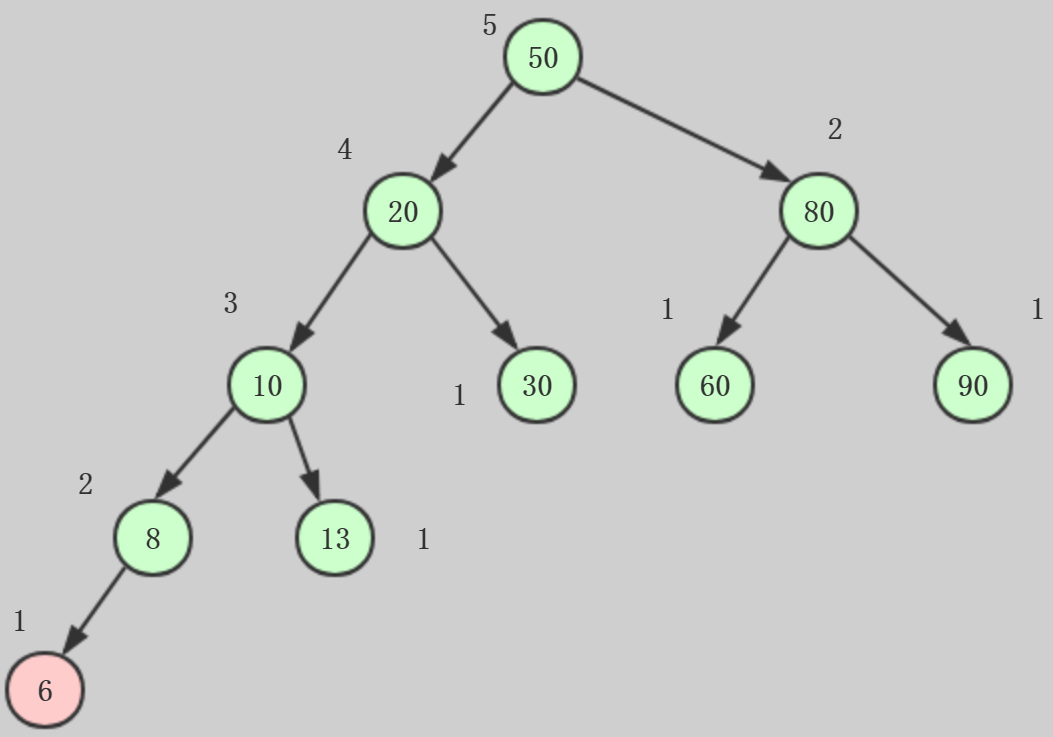
　　就已经不满足特征1了，为了平衡，我们需要标注节点的高度，如上图标注，节点高度=所有子树中最高的子树的高度+1，然后可以计算平衡因子，平衡因子=左子树的高度-右子树的高度，所以任意一个节点的平衡因子的绝对值 >= 2，这棵树就不是平衡二叉树了。

　　所以平衡因子就是是否平衡二叉树的判断标准。

实现节点高度和平衡因子计算：

private class Node {
	public K key;
	public V value;
	public Node left, right;
	private int height;

	public Node(K key, V value) {
		this.key = key;
		this.value = value;
		left = null;
		right = null;
		this.height = 1; //因为每次节点刚插入都是叶子节点，所以初始高度都是1
	}
}
//获得节点高度
private int getHeight(Node node) {
	if (node == null) {
		return 0;
	} else {
		return node.height;
	}
}
//获得节点平衡因子
private int getBalanceFactor(Node node) {
	if (node == null) {
		return 0;
	}
	return getHeight(node.left) - getHeight(node.right);
}

检查二分搜索树性质和平衡性:

//判断当前Tree是否为binary search tree
public boolean isBST() {
	ArrayList<K> keys = new ArrayList<>();
	infixOrder(root, keys); //中序遍历，如果是平衡二叉树，中序遍历就是升序
	for (int i = 0; i < keys.size(); i++) {
		if (keys.get(i-1).compareTo(keys.get(i)) > 0) { //如果当前node小于前一个node的值，返回false
			return false;
		}
	}
	return true;
}

private void infixOrder(Node node, ArrayList<K> keys) {
	if (node == null) {
		return;
	}
	infixOrder(node.left, keys);
	keys.add(node.key);
	infixOrder(node.right, keys);
}

//判断当前tree是否为平衡二叉树
public boolean isBalanced() {
	return isBalanced(root);
}

private boolean isBalanced(Node node) {
	if (node == null) {
		return true;
	}
	int isBalanced = getBalanceFactor(node);
	if (Math.abs(isBalanced) > 1) {
		return false;
	}
	return isBalanced(node.left) && isBalanced(node.right);
}

旋转操作基本原理(左旋和右旋)：

左旋转和右旋转是AVL树保证平衡的手段。

当新添加一个node，会影响其父节点或者祖先节点的平衡因子，所以我们需要沿着节点向上维护平衡性。

情形1：插入的节点在不平衡节点的左侧的左侧，也就是整体向左倾斜，需要进行右旋转。

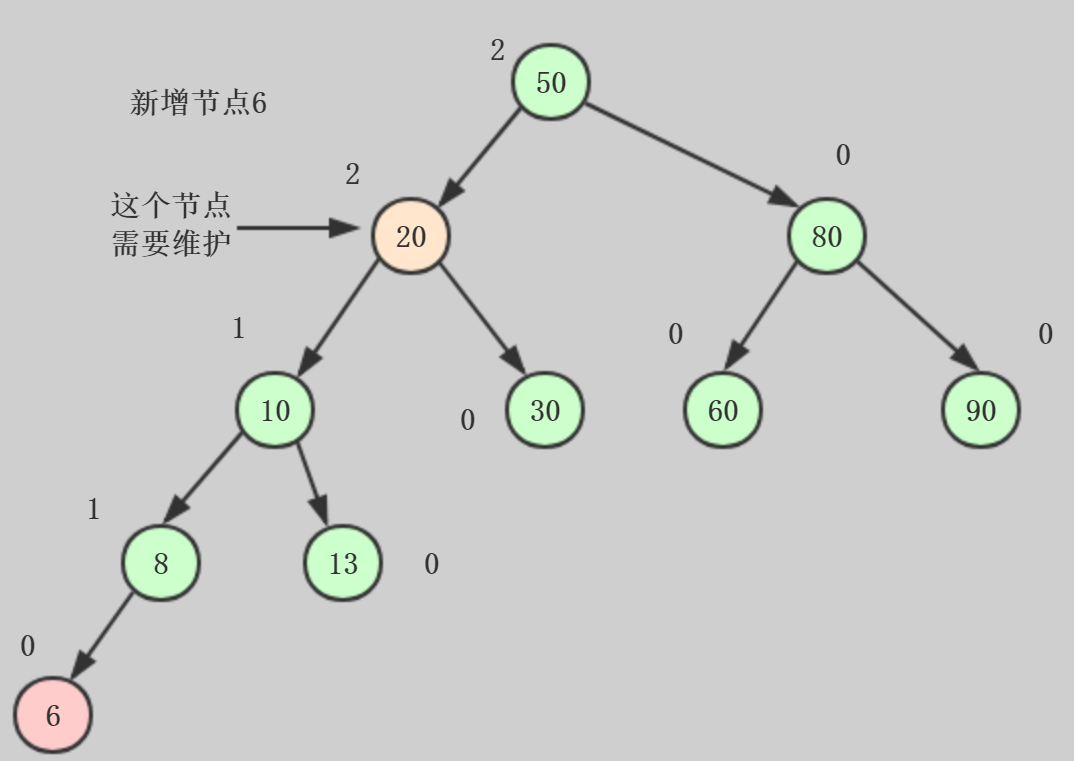
右旋过程：

　　我们沿着节点6向上寻找，直到找到节点20，平衡因子等于2，需要对节点20进行维护，进行右旋转的操作如下：

1、先把节点20的右子树断开。

2、将节点20的右子树等于节点50。

3、把节点20的原右子树变成接地那50的左子树。

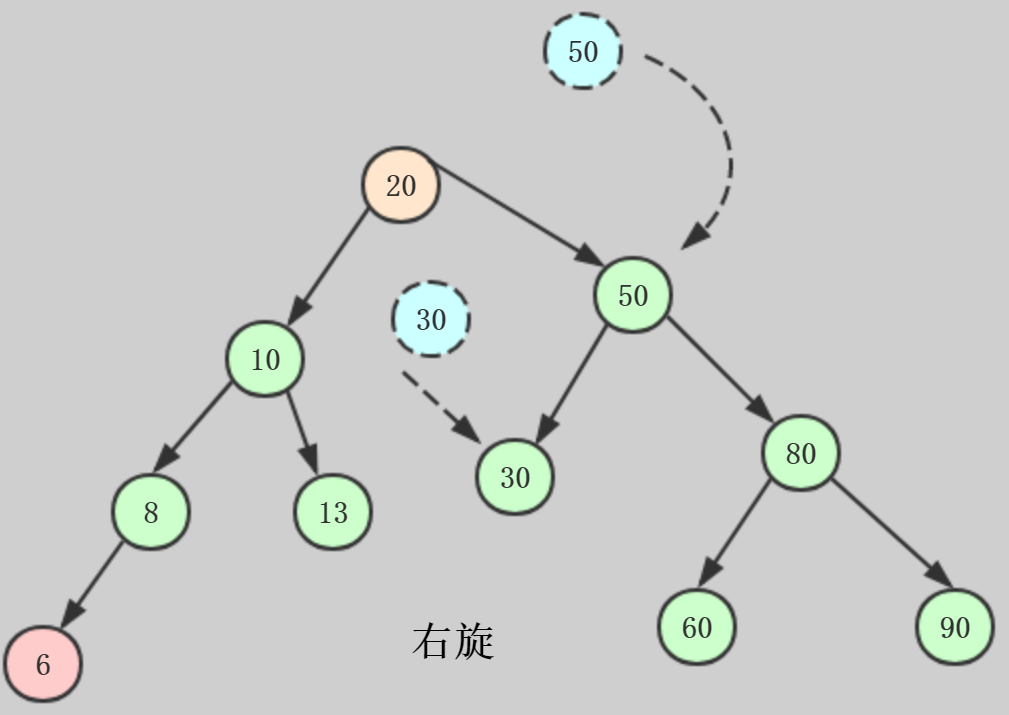
此时，这棵树既满足二分搜索树，又满足平衡二叉树。

情形2：插入的节点在不平衡节点的右侧的右侧，也就是整体向右倾斜，需要进行左旋转。

理解了右旋，左旋过程就很简单了，直接上图。

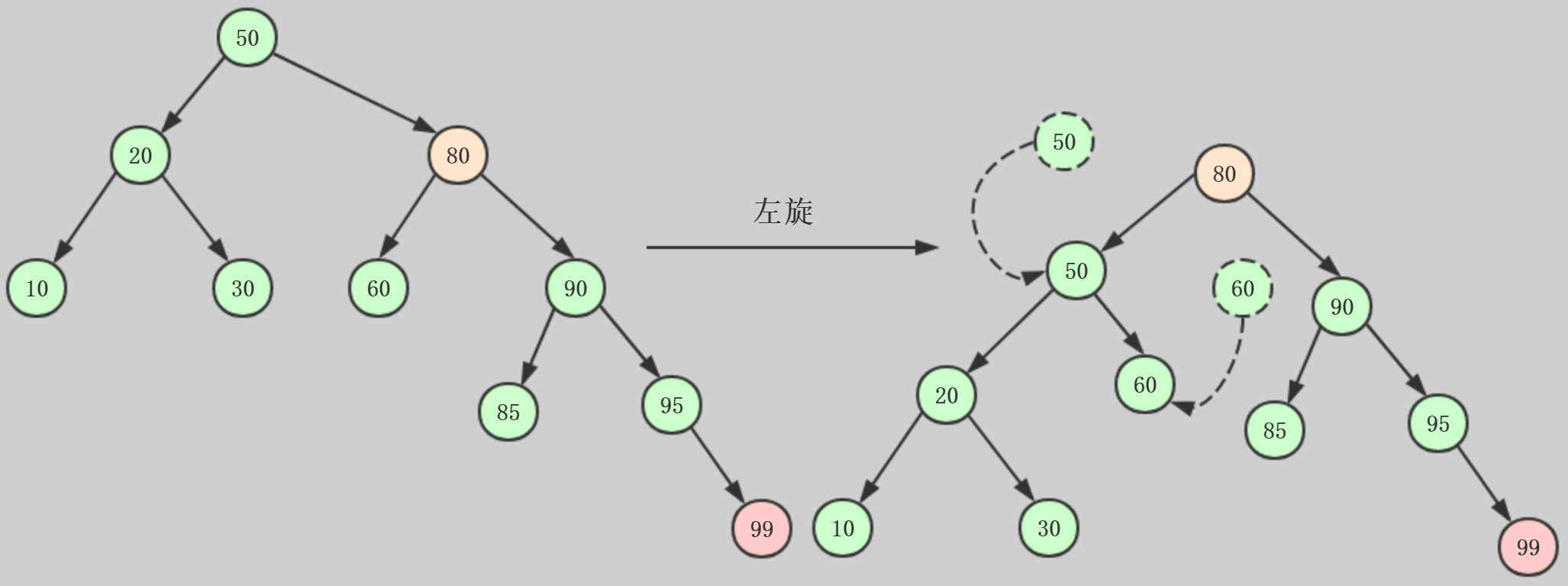
左旋和右旋示例代码：

/**
 * 实现右旋
 * y为需要右旋的节点
 * x为需要旋转节点的左子节点
 * z为target1的右子节点
 */
private Node rightRotate(Node y) {
	Node x = y.left;
	Node z = x.right;

	//右旋过程
	x.right = y;
	y.left = z;

	//更新height，只有target和target1的高度才会变化，需要先更新target的height，因为target1的height依赖target
	y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
	x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;

	return x;
}

/**
 * 实现右旋
 * y为需要左旋的节点
 * x为需要旋转节点的右子节点
 * z为target1的左子节点
 */
private Node leftRotate(Node y) {
	Node x = y.right;
	Node z = x.left;

	//右旋过程
	x.left = y;
	y.right = z;

	//更新height，只有target和target1的高度才会变化，需要先更新target的height，因为target1的height依赖target
	y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
	x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;

	return x;
}

// 向以node为根的二分搜索树中插入元素e，递归算法
// 返回插入新节点后二分搜索树的根
private Node add(Node node, K key, V value){

	if(node == null){
		size ++;
		return new Node(key, value);
	}

	if(key.compareTo(node.key) < 0)
		node.left = add(node.left, key, value);
	else if(key.compareTo(node.key) > 0)
		node.right = add(node.right, key, value);
	else
		node.value = value;

	//更新height
	node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;

	//计算平衡因子
	int balanceFactor = getBalanceFactor(node);
	if (Math.abs(balanceFactor) > 1) {
		System.out.println("current node is not balanced binary tree" + balanceFactor);
	}

	//平衡维护，balanceFactor > 1表示左子树高度大于右子树的高度，需要右旋
	if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
		return rightRotate(node);
	}

	//平衡维护，balanceFactor > 1表示右子树高度大于左子树的高度，需要左旋
	if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
		return leftRotate(node);
	}

	return node;
}

LR和RL：

在此之前说的两种情况实际上就是LL和RR，这里我们写一下LR和RL，对应着插入的节点在不平衡节点的左侧的右侧，以及右侧的左侧。

LR：

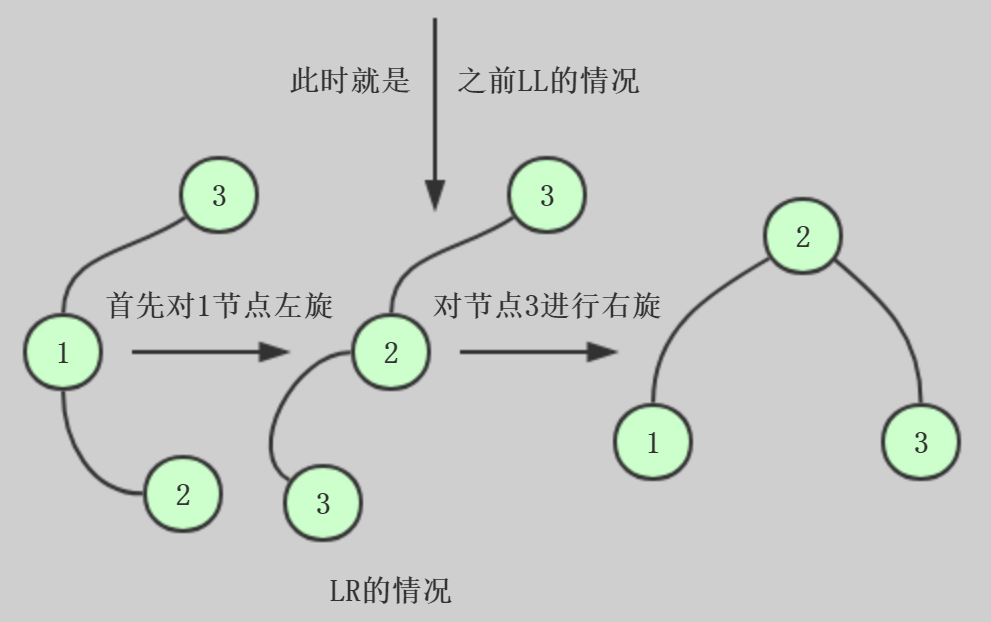
RL：

代码示例：

//LR
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
	node.left = leftRotate(node.left);
	return rightRotate(node);
}

//RL
if (balanceFactor < -1 && getBalanceFactor(node.right) < 0) {
	node.right = rightRotate(node.right);
	return leftRotate(node);
}

PS：

　　随机数据插入并查询的场景，AVL还是明显比二叉搜索树快，而在顺序/倒叙插入并查询，二叉搜索树效率严重下降，简直不能看，而AVL树效率依旧。

contains()：

// 看二分AVL树中是否包含元素key
public boolean contains(K key){
	return contains(root, key);
}

// 看以node为根的AVL树中是否包含元素value, 递归算法
private boolean contains(Node node, K key){

	if(node == null)
		return false;

	if(key.compareTo(node.key) == 0)
		return true;
	else if(key.compareTo(node.key) < 0)
		return contains(node.left, key);
	else // e.compareTo(node.key) > 0
		return contains(node.right, key);
}

删除元素：

// 从二分搜索树中删除元素为e的节点
public V remove(K key){
	Node node = getNode(root, key);
	if (node != null) {
		root = remove(root, key);
		return node.value;
	}
	return null;
}

// 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
// 返回删除节点后新的二分搜索树的根
Node remove(Node node, K key){

	if( node == null )
		return null;

	Node retNode; //保证平衡性，用于返回
	if( key.compareTo(node.key) < 0 ){
		node.left = remove(node.left , key);
		retNode = node;
	}
	else if(key.compareTo(node.key) > 0 ){
		node.right = remove(node.right, key);
		retNode = node;
	}
	else{
		// 待删除节点左子树为空的情况
		if(node.left == null){
			Node rightNode = node.right;
			node.right = null;
			size --;
			retNode = rightNode;
		}
		// 待删除节点右子树为空的情况
		else if(node.right == null){
			Node leftNode = node.left;
			node.left = null;
			size --;
			retNode = leftNode;
		} else {
			// 待删除节点左右子树均不为空的情况

			// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
			// 用这个节点顶替待删除节点的位置
			Node successor = minimum(node.right);
			successor.right = remove(node.right, successor.key);
			successor.left = node.left;

			node.left = node.right = null;
			retNode = successor;
		}
	}

	if (retNode == null) {
		return null;
	}
	//更新height
	retNode.height = Math.max(getHeight(retNode.left), getHeight(retNode.right)) + 1;

	//计算平衡因子
	int balanceFactor = getBalanceFactor(retNode);

	//平衡维护，balanceFactor > 1表示左子树高度大于右子树的高度，需要右旋
	//LL
	if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0) {
		return rightRotate(retNode);
	}

	//平衡维护，balanceFactor > 1表示右子树高度大于左子树的高度，需要左旋
	//RR
	if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0) {
		return leftRotate(retNode);
	}

	//LR
	if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
		retNode.left = leftRotate(retNode.left);
		return rightRotate(retNode);
	}

	//RL
	if (balanceFactor < -1 && getBalanceFactor(retNode.right) < 0) {
		retNode.right = rightRotate(retNode.right);
		return leftRotate(retNode);
	}

	return retNode;
}

private Node getNode(Node node, K key) {
	if( node == null )
		return null;

	if( key.compareTo(node.key) < 0 ){
		getNode(node.left, key);
	} else if(key.compareTo(node.key) > 0){
		getNode(node.right, key);
	} else {
		return node;
	}
	return null;
}

AVLTree.java完整代码：

public class AVLTree<K extends Comparable<K>, V> {

    private class Node {
        public K key;
        public V value;
        public Node left, right;
        private int height;

        public Node(K key, V value) {
            this.key = key;
            this.value = value;
            left = null;
            right = null;
            this.height = 1; //因为每次节点刚插入都是叶子节点，高度都是1
        }
    }

    private Node root;
    private int size;

    public AVLTree(){
        root = null;
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    //判断当前Tree是否为binary search tree
    public boolean isBST() {
        ArrayList<K> keys = new ArrayList<>();
        infixOrder(root, keys); //中序遍历，如果是平衡二叉树，中序遍历就是升序
        for (int i = 0; i < keys.size(); i++) {
            if (keys.get(i-1).compareTo(keys.get(i)) > 0) { //如果当前node小于前一个node的值，返回false
                return false;
            }
        }
        return true;
    }

    private void infixOrder(Node node, ArrayList<K> keys) {
        if (node == null) {
            return;
        }
        infixOrder(node.left, keys);
        keys.add(node.key);
        infixOrder(node.right, keys);
    }

    //判断当前tree是否为平衡二叉树
    public boolean isBalanced() {
        return isBalanced(root);
    }

    private boolean isBalanced(Node node) {
        if (node == null) {
            return true;
        }
        int isBalanced = getBalanceFactor(node);
        if (Math.abs(isBalanced) > 1) {
            return false;
        }
        return isBalanced(node.left) && isBalanced(node.right);
    }

    //获得节点高度
    private int getHeight(Node node) {
        if (node == null) {
            return 0;
        } else {
            return node.height;
        }
    }
    //获得节点平衡因子
    private int getBalanceFactor(Node node) {
        if (node == null) {
            return 0;
        }
        return getHeight(node.left) - getHeight(node.right);
    }

    // 向二分搜索树中添加新的元素e
    public void add(K key, V value){
        root = add(root, key, value);
    }

    /**
     * 实现右旋
     * y为需要右旋的节点
     * x为需要旋转节点的左子节点
     * z为target1的右子节点
     */
    private Node rightRotate(Node y) {
        Node x = y.left;
        Node z = x.right;

        //右旋过程
        x.right = y;
        y.left = z;

        //更新height，只有target和target1的高度才会变化，需要先更新target的height，因为target1的height依赖target
        y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
        x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;

        return x;
    }

    /**
     * 实现右旋
     * y为需要左旋的节点
     * x为需要旋转节点的右子节点
     * z为target1的左子节点
     */
    private Node leftRotate(Node y) {
        Node x = y.right;
        Node z = x.left;

        //右旋过程
        x.left = y;
        y.right = z;

        //更新height，只有target和target1的高度才会变化，需要先更新target的height，因为target1的height依赖target
        y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
        x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;

        return x;
    }

    // 向以node为根的二分搜索树中插入元素e，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, K key, V value){

        if(node == null){
            size ++;
            return new Node(key, value);
        }

        if(key.compareTo(node.key) < 0)
            node.left = add(node.left, key, value);
        else if(key.compareTo(node.key) > 0)
            node.right = add(node.right, key, value);
        else
            node.value = value;

        //更新height
        node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;

        //计算平衡因子
        int balanceFactor = getBalanceFactor(node);

        //平衡维护，balanceFactor > 1表示左子树高度大于右子树的高度，需要右旋
        //LL
        if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
            return rightRotate(node);
        }

        //平衡维护，balanceFactor > 1表示右子树高度大于左子树的高度，需要左旋
        //RR
        if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
            return leftRotate(node);
        }

        //LR
        if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
            node.left = leftRotate(node.left);
            return rightRotate(node);
        }

        //RL
        if (balanceFactor < -1 && getBalanceFactor(node.right) < 0) {
            node.right = rightRotate(node.right);
            return leftRotate(node);
        }

        return node;
    }

    // 看二分AVL树中是否包含元素key
    public boolean contains(K key){
        return contains(root, key);
    }

    // 看以node为根的AVL树中是否包含元素value, 递归算法
    private boolean contains(Node node, K key){

        if(node == null)
            return false;

        if(key.compareTo(node.key) == 0)
            return true;
        else if(key.compareTo(node.key) < 0)
            return contains(node.left, key);
        else // e.compareTo(node.key) > 0
            return contains(node.right, key);
    }

    // 寻找二分搜索树的最小元素
    public V minimum(){
        if(size == 0)
            throw new IllegalArgumentException("BST is empty!");

        return minimum(root).value;
    }

    // 返回以node为根的二分搜索树的最小值所在的节点
    private Node minimum(Node node){
        if(node.left == null)
            return node;
        return minimum(node.left);
    }

    // 寻找二分搜索树的最大元素
    public V maximum(){
        if(size == 0)
            throw new IllegalArgumentException("BST is empty");

        return maximum(root).value;
    }

    // 返回以node为根的二分搜索树的最大值所在的节点
    private Node maximum(Node node){
        if(node.right == null)
            return node;

        return maximum(node.right);
    }

    // 从二分搜索树中删除元素为e的节点
    public V remove(K key){
        Node node = getNode(root, key);
        if (node != null) {
            root = remove(root, key);
            return node.value;
        }
        return null;
    }

    // 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
    // 返回删除节点后新的二分搜索树的根
    Node remove(Node node, K key){

        if( node == null )
            return null;

        Node retNode; //保证平衡性，用于返回
        if( key.compareTo(node.key) < 0 ){
            node.left = remove(node.left , key);
            retNode = node;
        }
        else if(key.compareTo(node.key) > 0 ){
            node.right = remove(node.right, key);
            retNode = node;
        }
        else{
            // 待删除节点左子树为空的情况
            if(node.left == null){
                Node rightNode = node.right;
                node.right = null;
                size --;
                retNode = rightNode;
            }
            // 待删除节点右子树为空的情况
            else if(node.right == null){
                Node leftNode = node.left;
                node.left = null;
                size --;
                retNode = leftNode;
            } else {
                // 待删除节点左右子树均不为空的情况

                // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
                // 用这个节点顶替待删除节点的位置
                Node successor = minimum(node.right);
                successor.right = remove(node.right, successor.key);
                successor.left = node.left;

                node.left = node.right = null;
                retNode = successor;
            }
        }

        if (retNode == null) {
            return null;
        }
        //更新height
        retNode.height = Math.max(getHeight(retNode.left), getHeight(retNode.right)) + 1;

        //计算平衡因子
        int balanceFactor = getBalanceFactor(retNode);

        //平衡维护，balanceFactor > 1表示左子树高度大于右子树的高度，需要右旋
        //LL
        if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0) {
            return rightRotate(retNode);
        }

        //平衡维护，balanceFactor > 1表示右子树高度大于左子树的高度，需要左旋
        //RR
        if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0) {
            return leftRotate(retNode);
        }

        //LR
        if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
            retNode.left = leftRotate(retNode.left);
            return rightRotate(retNode);
        }

        //RL
        if (balanceFactor < -1 && getBalanceFactor(retNode.right) < 0) {
            retNode.right = rightRotate(retNode.right);
            return leftRotate(retNode);
        }

        return retNode;
    }

    private Node getNode(Node node, K key) {
        if( node == null )
            return null;

        if( key.compareTo(node.key) < 0 ){
            getNode(node.left, key);
        } else if(key.compareTo(node.key) > 0){
            getNode(node.right, key);
        } else {
            return node;
        }
        return null;
    }

    @Override
    public String toString(){
        StringBuilder res = new StringBuilder();
        generateBSTString(root, 0, res);
        return res.toString();
    }

    // 生成以node为根节点，深度为depth的描述二叉树的字符串
    private void generateBSTString(Node node, int depth, StringBuilder res){

        if(node == null){
            res.append(generateDepthString(depth) + "null\n");
            return;
        }

        res.append(generateDepthString(depth) + node.key +"\n");
        generateBSTString(node.left, depth + 1, res);
        generateBSTString(node.right, depth + 1, res);
    }

    private String generateDepthString(int depth){
        StringBuilder res = new StringBuilder();
        for(int i = 0 ; i < depth ; i ++)
            res.append("--");
        return res.toString();
    }
}