MITx - 6.00.2x 笔记(Unit1 Lecture 3 Graph Problems)
Lecture 3 Graph Problems
Graph Theory(图论)
图论是数学的一个分支,它以图为研究对象,研究顶点和边组成的图形的数学理论和方法。nodes, edges
现实世界中很多事物都是有联系的,因此图论特别适合于解决现实问题。
可应用于路径规划
Adjacency List(邻接表)
在图论中,邻接表代表一个图中的所有边或弧。
如果是无向图,那么每条边由两个结点组成,分别代表边的两个端点;如果是有向图,那么每条边是一个结点对,分别代表边的始点和终点。一般来说,邻接表是无向的。
# 定义Node class而不直接使用string
# 因为可能会涉及拥有多个属性的对象
# 定义节点
class Node(object):
def __init__(self, name):
"""Assume name is a string"""
self.name = name
def getName(self):
return self.name
def __str__(self):
return self.name
# 定义路径(起点src, 终点dest)
class Edge(object):
def __init__(self, src, dest):
"""Assumes src and dest are nodes,
src -> dest """
self.src = src
self.dest = dest
def getSource(self):
return self.src
def getDestination(self):
return self.dest
def __str__(self):
return self.src.getName() + '->' + self.dest.getName()
# 绘制模块
class Digraph(object):
"""edges is a dict mapping each node to a list of children"""
def __init__(self):
self.edges = []
def addNode(self, node):
if node in self.edges:
raise ValueError('Duplicate node')
else:
self.edges[node] = []
def addEdge(self, edge):
src = edge.getSource()
dest = edge.getDestination()
if not (src in self.edges and dest in self.edges):
raise ValueError('Node not in graph')
self.edges[src].append(dest)
def childrenOf(self, node):
return self.edges[node]
def hasNode(self, node):
return node in self.edges
def getNode(self, name):
for n in self.edges:
if n.getName() == name:
return n
raise NameError(name)
def __str__(self):
result = ''
for src in self.edges:
for dest in self.edges[src]:
result = result + src.getName() + ' -> ' + dest.getName() + '\n'
return result[:-1] # omit final newline
class Graph(Digraph):
def addEdge(self, edge):
Digraph.addEdge(self, edge)
rev = Edge(edge.getDestination(), edge.getSource())
Digraph.addEdge(self, rev)
# Digraph addEdge add TWO edges, one for each direction- 寻找节点n1到n2的最短路径的基本规则:
- 第一edge的起点为n1
- 最后一条edge的终点为n2
- 如果e2跟在e1之后,那么e2的起点是e1的终点
- 目标:尽可能减少edges的数量
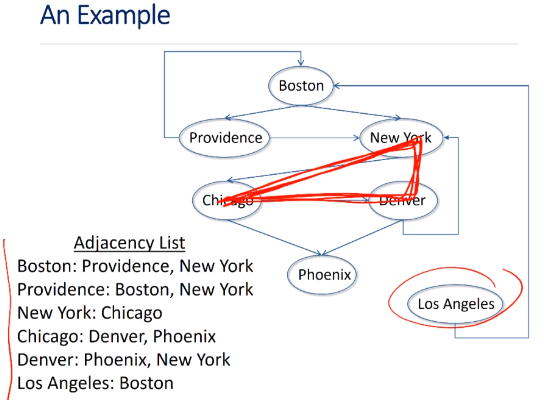
def buildCityGraph(graphType):
g = graphType()
for name in ('Boston', 'Providence', 'New York', 'Chicago',
'Denver', 'Phoenix', 'Los Angeles'): #Create 7 nodes
g.addNode(Node(name))
g.addEdge(Edge(g.getNode('Boston'), g.getNode('Providence')))
g.addEdge(Edge(g.getNode('Boston'), g.getNode('New York')))
g.addEdge(Edge(g.getNode('Providence'), g.getNode('Boston')))
g.addEdge(Edge(g.getNode('Providence'), g.getNode('New York')))
g.addEdge(Edge(g.getNode('New York'), g.getNode('Chicago')))
g.addEdge(Edge(g.getNode('Chicago'), g.getNode('Denver')))
g.addEdge(Edge(g.getNode('Denver'), g.getNode('Phoenix')))
g.addEdge(Edge(g.getNode('Denver'), g.getNode('New York')))
g.addEdge(Edge(g.getNode('Los Angeles'), g.getNode('Boston')))
return g# In:
print('Digraph:')
print(buildCityGraph(Digraph))
# Out:
Digraph:
Boston -> Providence
Boston -> New York
Providence -> Boston
Providence -> New York
New York -> Chicago
Chicago -> Denver
Denver -> Phoenix
Denver -> New York
Los Angeles -> BostonDepth-first Search (DFS,深度优先搜索)
先找准一个节点,搜索所有可能路径,遍历顺序图示:

def printPath(path):
"""Assumes path is a list of nodes"""
result = ''
for i in range(len(path)):
result = result + str(path[i])
if i != len(path) - 1:
result = result + '->'
return result
def DFS(graph, start, end, path, shortest, toPrint = False):
"""Assumes graph is a Digraph; start and end are nodes;
path and shortest are lists of nodes
Returns a shortest path from start to end in graph"""
path = path + [start]
if toPrint:
print('Current DFS path:', printPath(path))
if start == end:
return path
for node in graph.childrenOf(start):
if node not in path: #avoid cycles
if shortest == None or len(path) < len(shortest):
newPath = DFS(graph, node, end, path, shortest,
toPrint)
if newPath != None:
shortest = newPath
elif toPrint:
print('Already visited', node)
return shortest
def shortestPath(graph, start, end, toPrint = False):
"""Assumes graph is a Digraph; start and end are nodes
Returns a shortest path from start to end in graph"""
return DFS(graph, start, end, [], None, toPrint)
def testSP(source, destination):
g = buildCityGraph(Digraph)
sp = shortestPath(g, g.getNode(source), g.getNode(destination),
toPrint = True)
if sp != None:
print('Shortest path from', source, 'to',
destination, 'is', printPath(sp))
else:
print('There is no path from', source, 'to', destination)
testSP('Chicago', 'Boston')# Out:
Current DFS path: Chicago
Current DFS path: Chicago->Phoenix
Current DFS path: Chicago->Denver
Current DFS path: Chicago->Denver->Phoenix
Current DFS path: Chicago->Denver->New York
Already visited Chicago
There is no path from Chicago to Boston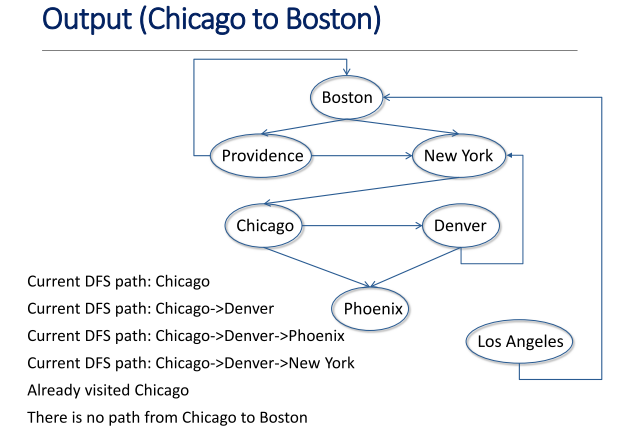
Breadth-first Search (BFS,广度优先搜索)
图示:

回到例题
找到一篇博文:图的遍历之 深度优先搜索和广度优先搜索
小结





