BZOJ2127: happiness

2127: happiness

Time Limit: 51 Sec Memory Limit: 259 MB
Submit: 2700 Solved: 1299
[Submit][Status][Discuss]

Description

高一一班的座位表是个n*m的矩阵，经过一个学期的相处，每个同学和前后左右相邻的同学互相成为了好朋友。这学期要分文理科了，每个同学对于选择文科与理科有着自己的喜悦值，而一对好朋友如果能同时选文科或者理科，那么他们又将收获一些喜悦值。作为计算机竞赛教练的scp大老板，想知道如何分配可以使得全班的喜悦值总和最大。

Input

第一行两个正整数n，m。接下来是六个矩阵第一个矩阵为n行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择文科获得的喜悦值。第二个矩阵为n行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学选择理科获得的喜悦值。第三个矩阵为n-1行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择文科获得的额外喜悦值。第四个矩阵为n-1行m列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i+1行第j列的同学同时选择理科获得的额外喜悦值。第五个矩阵为n行m-1列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择文科获得的额外喜悦值。第六个矩阵为n行m-1列 此矩阵的第i行第j列的数字表示座位在第i行第j列的同学与第i行第j+1列的同学同时选择理科获得的额外喜悦值。

Output

输出一个整数，表示喜悦值总和的最大值

Sample Input

1 2

1 1

100 110

1

1000

Sample Output

1210

【样例说明】

两人都选理，则获得100+110+1000的喜悦值。

【数据规模】

对于100%以内的数据，n,m<=100 所有喜悦值均为小于等于5000的非负整数

题解

引用黄学长的一句话

做完我整个人都最小割了

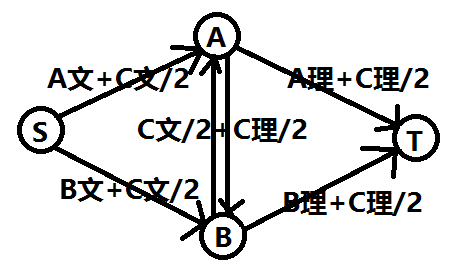
考虑总量为 \(A_文 + A_理 + B_文 + B_理 + C_文 + C_理\)，减去最小割即为答案
分情况\(A\)文\(B\)理，\(B\)文\(A\)理，\(2\)文，\(2\)理，看看割会什么样
看看有多少中割，分别对应哪些情况

注意虽然图中\(S\)向\(A\)、\(B\)，\(A\)、\(B\)向\(T\)采用“\(A_X + \frac{C_X}{2}\)”的形式，但真这么连会多算\(A_X\)，应该把\(A_X\)和\(\frac{C_X}{2}\)拆成两条边
感性理解一下。。。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <map>
#include <cmath>
inline long long max(long long a, long long b){return a > b ? a : b;}
inline long long min(long long a, long long b){return a < b ? a : b;}
inline long long abs(long long x){return x < 0 ? -x : x;}
inline void swap(long long &x, long long &y){long long tmp = x;x = y;y = tmp;}
inline void read(long long &x)
{
    x = 0;char ch = getchar(), c = ch;
    while(ch < '0' || ch > '9') c = ch, ch = getchar();
    while(ch <= '9' && ch >= '0') x = x * 10 + ch - '0', ch = getchar();
    if(c == '-') x = -x;
}
const long long INF = 0x3f3f3f3f3f3f3f3f;
struct Edge
{
	long long u,v,w,nxt;
	Edge(long long _u, long long _v, long long _w, long long _nxt){u = _u;v = _v;w = _w;nxt = _nxt;}
	Edge(){}
}edge[1000010];
long long head[100010], cnt = 1, S, T, q[100010], he, ta, h[100010], ans;
inline void insert(long long a, long long b, long long c)
{
	edge[++ cnt] = Edge(a, b, c, head[a]), head[a] = cnt;
	edge[++ cnt] = Edge(b, a, 0, head[b]), head[b] = cnt;
}
bool bfs()
{
	memset(h, -1, sizeof(h)), h[S] = 0, he = ta = 0, q[ta ++] = S;
	while(he < ta)
	{
		long long now = q[he ++];
		for(long long pos = head[now];pos;pos = edge[pos].nxt)
		{
			long long v = edge[pos].v;
			if(edge[pos].w && h[v] == -1)
				h[v] = h[now] + 1, q[ta ++] = v;
		}
	}
	return h[T] != -1;
}
long long dfs(long long x, long long f)
{
	if(x == T) return f;
	long long used = 0, w;
	for(long long pos = head[x];pos;pos = edge[pos].nxt)
	{
		long long v = edge[pos].v;
		if(h[v] == h[x] + 1)
		{
			w = dfs(v, min(edge[pos].w, f - used));
			edge[pos].w -= w;
			edge[pos ^ 1].w += w;
			used += w;
			if(used == f) return f;
		}
	}
	if(!used) h[x] = -1;
	return used;
}
void dinic()
{
	while(bfs()) ans += dfs(S, INF);
}
long long n, m, sum, tot, wen[201][201], li[201][201], num[201][201],twenh[201][201],tlih[201][201],twenl[201][201],tlil[201][201];
int main()
{
	read(n), read(m);
	for(long long i = 1;i <= n;++ i) 
		for(long long j = 1;j <= m;++ j)
			read(wen[i][j]), sum += wen[i][j], num[i][j] = ++ tot;
	S = tot + 1, T = S + 1;
	for(long long i = 1;i <= n;++ i)
		for(long long j = 1;j <= m;++ j)
			read(li[i][j]), sum += li[i][j];
	for(long long i = 1;i < n;++ i)
		for(long long j = 1;j <= m;++ j)
			read(twenh[i][j]), sum += twenh[i][j];
	for(long long i = 1;i < n;++ i)
		for(long long j = 1;j <= m;++ j)
			read(tlih[i][j]), sum += tlih[i][j];
	for(long long i = 1;i <= n;++ i)
		for(long long j = 1;j < m;++ j)
			read(twenl[i][j]), sum += twenl[i][j];
	for(long long i = 1;i <= n;++ i)
		for(long long j = 1;j < m;++ j)
			read(tlil[i][j]), sum += tlil[i][j];
	for(long long i = 1;i <= n;++ i)
		for(long long j = 1;j <= m;++ j)
			insert(S, num[i][j], wen[i][j] << 1), insert(num[i][j], T, li[i][j] << 1);
	for(long long i = 1;i < n;++ i)
		for(long long j = 1;j <= m;++ j)
			insert(S, num[i][j], twenh[i][j]), insert(num[i][j], T, tlih[i][j]), 
			insert(S, num[i + 1][j], twenh[i][j]), insert(num[i + 1][j], T, tlih[i][j]),
			insert(num[i][j], num[i + 1][j], twenh[i][j] + tlih[i][j]),
			insert(num[i + 1][j], num[i][j], twenh[i][j] + tlih[i][j]);
	for(long long i = 1;i <= n;++ i)
		for(long long j = 1;j < m;++ j)
			insert(S, num[i][j], twenl[i][j]), insert(num[i][j], T, tlil[i][j]), 
			insert(S, num[i][j + 1], twenl[i][j]), insert(num[i][j + 1], T, tlil[i][j]),
			insert(num[i][j], num[i][j + 1], twenl[i][j] + tlil[i][j]),
			insert(num[i][j + 1], num[i][j], twenl[i][j] + tlil[i][j]);
	dinic();
	printf("%lld", sum - (ans >> 1));
    return 0;
}