Uva11729 Commando War

“Waiting for orders we held in the wood, word from the front never came By evening the sound of the gunfire was miles away Ah softly we moved through the shadows, slip away through the trees Crossing their lines in the mists in the fields on our hands and our knees And all that I ever, was able to see The fire in the air, glowing red, silhouetting the smoke on the breeze” There is a war and it doesn’t look very promising for your country. Now it’s time to act. You have a commando squad at your disposal and planning an ambush on an important enemy camp located nearby. You have N soldiers in your squad. In your master-plan, every single soldier has a unique responsibility and you don’t want any of your soldier to know the plan for other soldiers so that everyone can focus on his task only. In order to enforce this, you brief every individual soldier about his tasks separately and just before sending him to the battlefield. You know that every single soldier needs a certain amount of time to execute his job. You also know very clearly how much time you need to brief every single soldier. Being anxious to finish the total operation as soon as possible, you need to find an order of briefing your soldiers that will minimize the time necessary for all the soldiers to complete their tasks. You may assume that, no soldier has a plan that depends on the tasks of his fellows. In other words, once a soldier begins a task, he can finish it without the necessity of pausing in between. Input There will be multiple test cases in the input file. Every test case starts with an integer N (1 ≤ N ≤ 1000), denoting the number of soldiers. Each of the following N lines describe a soldier with two integers B (1 ≤ B ≤ 10000) & J (1 ≤ J ≤ 10000). B seconds are needed to brief the soldier while completing his job needs J seconds. The end of input will be denoted by a case with N = 0. This case should not be processed. Output For each test case, print a line in the format, ‘Case X: Y ’, where X is the case number & Y is the total number of seconds counted from the start of your first briefing till the completion of all jobs. Sample Input 3 2 5 3 2 2 1 3 3 3 4 4 5 5 0 Sample Output Case 1: 8 Case 2: 15

【题解】

可以肯定，交代任务的时间是一定的。

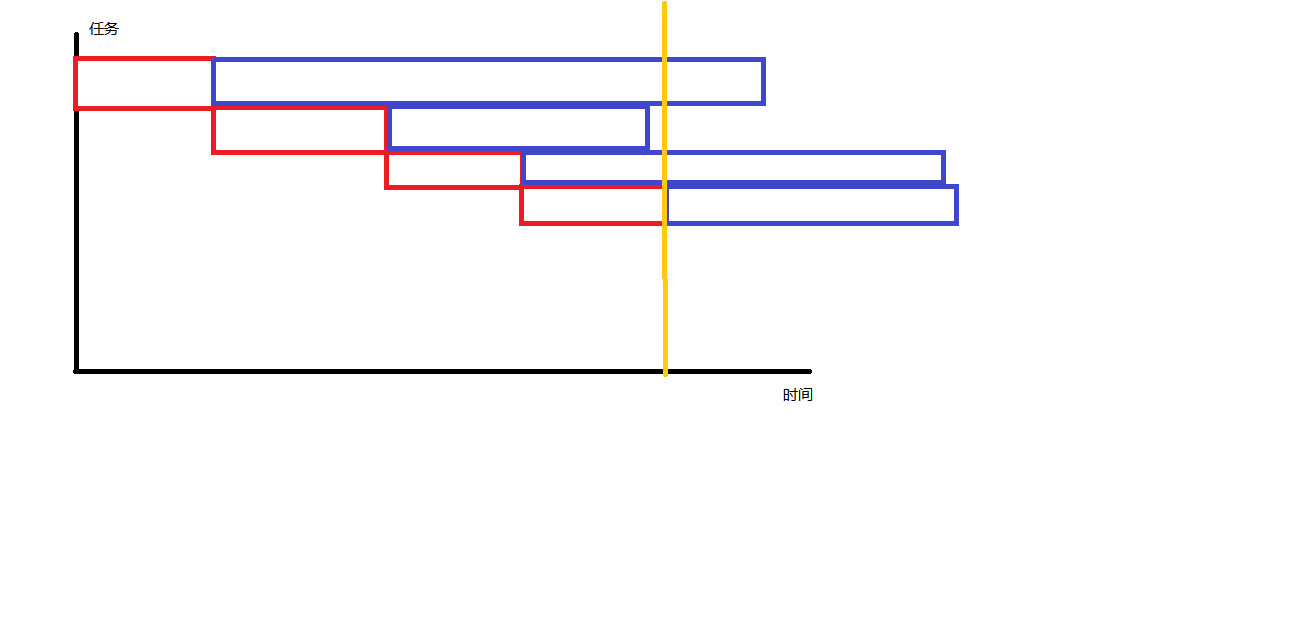
我们把每个任务的交代和完成时间画一个柱状图，红色代表交代时间，蓝色代表执行时间

不难发现最终完成时间取决于黄色线条伸出的部分

因此越长的蓝色越靠前越好

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#define max(a, b) ((a) > (b) ? (a) : (b))
#define min(a, b) ((a) < (b) ? (a) : (b))
inline void swap(int &a, int &b)
{
    int tmp = a;a = b;b = tmp;
}
inline void read(int &x)
{
    x = 0;char ch = getchar(), c = ch;
    while(ch < '0' || ch > '9')c = ch, ch = getchar();
    while(ch <= '9' && ch >= '0')x = x * 10 + ch - '0', ch = getchar();
    if(c == '-')x = -x;
}

const int MAXN = 1000 + 10;

struct Node
{
    int b,j;
}node[MAXN];

int cmp(Node a, Node b)
{
    return a.j > b.j;
}

int n; 

int main()
{
    int t = 0;
    while(scanf("%d", &n) != EOF && n)
    {
        ++ t;
        for(register int i = 1;i <= n;++ i)
            read(node[i].b), read(node[i].j);
        std::sort(node + 1, node + 1 + n, cmp);
        int ma = 0, now = 0;
        for(register int i = 1;i <= n;++ i)
            now += node[i].b, ma = max(ma, now + node[i].j);
        printf("Case %d: %d\n", t, ma);
    }
    return 0;
}