POJ1692 Crossed Matchings

Crossed Matchings

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 2954		Accepted: 1918

Description

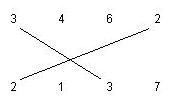
There are two rows of positive integer numbers. We can draw one line segment between any two equal numbers, with values r, if one of them is located in the first row and the other one is located in the second row. We call this line segment an r-matching segment. The following figure shows a 3-matching and a 2-matching segment.

We want to find the maximum number of matching segments possible to draw for the given input, such that:
1. Each a-matching segment should cross exactly one b-matching segment, where a != b .
2. No two matching segments can be drawn from a number. For example, the following matchings are not allowed.

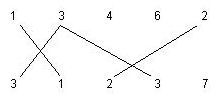
Write a program to compute the maximum number of matching segments for the input data. Note that this number is always even.

Input

The first line of the input is the number M, which is the number of test cases (1 <= M <= 10). Each test case has three lines. The first line contains N1 and N2, the number of integers on the first and the second row respectively. The next line contains N1 integers which are the numbers on the first row. The third line contains N2 integers which are the numbers on the second row. All numbers are positive integers less than 100.

Output

Output should have one separate line for each test case. The maximum number of matching segments for each test case should be written in one separate line.

Sample Input

3
6 6
1 3 1 3 1 3
3 1 3 1 3 1
4 4
1 1 3 3 
1 1 3 3 
12 11
1 2 3 3 2 4 1 5 1 3 5 10
3 1 2 3 2 4 12 1 5 5 3 

Sample Output

6
0
8

Source

Tehran 1999

 

【题解】

dp[i][j]表示num1前i个，num2前j个的最大匹配数（突然有种二分图的感觉）

dp[i][j] = max(dp[i-1][j],dp[i][j-1], dp[u][v] + 2 && num1[u + 1] == num2[j] && num1[i] == num2[v + 1] && num1[i] != num2[j])

不难发现选择的线段越靠后越好，于是可以预处理u和v

On^2

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#define max(a, b) ((a) > (b) ? (a) : (b))

inline void read(int &x)
{
    x = 0;char ch = getchar(), c = ch;
    while(ch < '0' || ch > '9')c = ch, ch = getchar();
    while(ch <= '9' && ch >= '0')x = x * 10 + ch - '0', ch = getchar();
    if(c == '-')x = -x;
}

const int INF = 0x3f3f3f3f;
const int MAXN = 200 + 10;

int t,n1,n2,num1[MAXN], num2[MAXN], dp[MAXN][MAXN], iclose[MAXN][MAXN],jclose[MAXN][MAXN];

/*
iclose[i][j]表示与num2[j]相等的最近的前i-1个num1的下标
jclose[i][j]表示与num1[i]相等的最近的前j-1个num2的下标 
*/

int main()
{
    read(t);
    for(;t;--t)
    {
        read(n1), read(n2);
        for(register int i = 1;i <= n1;++ i) read(num1[i]);
        for(register int i = 1;i <= n2;++ i) read(num2[i]);
        for(register int i = 1;i <= n1;++ i)
            for (register int j = 1;j <= n2;++ j)
                if(num1[i - 1] == num2[j]) iclose[i][j] = i - 1;
                else iclose[i][j] = iclose[i - 1][j]; 
        for(register int i = 1;i <= n1;++ i)
            for (register int j = 1;j <= n2;++ j)
                if(num1[i] == num2[j - 1]) jclose[i][j] = j - 1;
                else jclose[i][j] = jclose[i][j - 1]; 
        for(register int i = 1;i <= n1;++ i)
            for(register int j = 1;j <= n2;++ j)
            {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                if(num1[i] != num2[j] && iclose[i][j] > 0 && jclose[i][j] > 0)dp[i][j] = max(dp[i][j],dp[iclose[i][j] - 1][jclose[i][j] - 1] + 2);
            }
        printf("%d\n", dp[n1][n2]);
    }
    return 0;
}