BZOJ2427: [HAOI2010]软件安装
2427: [HAOI2010]软件安装
Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 1512 Solved: 584
[Submit][Status][Discuss]
Description
现在我们的手头有N个软件,对于一个软件i,它要占用Wi的磁盘空间,它的价值为Vi。我们希望从中选择一些软件安装到一台磁盘容量为M计算机上,使得这些软件的价值尽可能大(即Vi的和最大)。
但是现在有个问题:软件之间存在依赖关系,即软件i只有在安装了软件j(包括软件j的直接或间接依赖)的情况下才能正确工作(软件i依赖软件j)。幸运的是,一个软件最多依赖另外一个软件。如果一个软件不能正常工作,那么它能够发挥的作用为0。
我们现在知道了软件之间的依赖关系:软件i依赖软件Di。现在请你设计出一种方案,安装价值尽量大的软件。一个软件只能被安装一次,如果一个软件没有依赖则Di=0,这时只要这个软件安装了,它就能正常工作。
Input
第1行:N, M (0<=N<=100, 0<=M<=500)
第2行:W1, W2, ... Wi, ..., Wn (0<=Wi<=M )
第3行:V1, V2, ..., Vi, ..., Vn (0<=Vi<=1000 )
第4行:D1, D2, ..., Di, ..., Dn(0<=Di<=N, Di≠i )
Output
一个整数,代表最大价值。
Sample Input
3 10
5 5 6
2 3 4
0 1 1
5 5 6
2 3 4
0 1 1
Sample Output
5
HINT
Source
【题解】
先缩点。
两种解法。
‘’1、若把当前图中的每个结点成1个物品,磁盘空间当成背包,则类似有依赖关系的背包问题,可以用动态规划解决。
将所有的树重新编号,设共有x棵树,每棵树的根结点的编号r[1],r[2],…,r[x];
设f(r[i],j)表示第i棵树前拥有j的资源,则
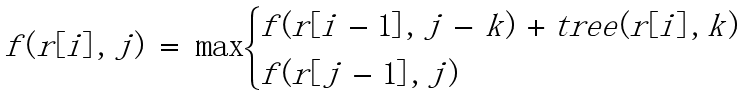
tree(r[i],k)表示第i棵树拥有k资源的最大代价,这个值可以用上述公式处理即,去掉根后转化森林,用背包问题解决。
1<=i<=N, 0<=k<=j<=M
时间复杂度O(NM2)
将所有的树重新编号,设共有x棵树,每棵树的根结点的编号r[1],r[2],…,r[x];
设f(r[i],j)表示第i棵树前拥有j的资源,则
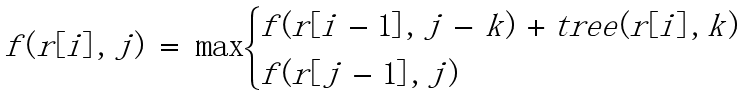
tree(r[i],k)表示第i棵树拥有k资源的最大代价,这个值可以用上述公式处理即,去掉根后转化森林,用背包问题解决。
1<=i<=N, 0<=k<=j<=M
时间复杂度O(NM2)
2、将森林转化为二叉树后,采用树型动态规划一次求出。


设f(i,j)表示以i为根结点的二叉树分配j资源的最大价值
 ‘’
‘’——by 朱全民
这里采用第二种
做得时候注意,森林->二叉树要虚一个空节点作为根,不能任选一棵树的根作根(被卡了四个点)

1 #include <iostream> 2 #include <cstdio> 3 #include <cstdlib> 4 #include <cstring> 5 #include <cmath> 6 #include <algorithm> 7 #define min(a, b) ((a) < (b) ? (a) : (b)) 8 #define max(a, b) ((a) > (b) ? (a) : (b)) 9 10 inline void read(int &x) 11 { 12 x = 0;char ch = getchar(), c = ch; 13 while(ch < '0' || ch > '9')c = ch, ch = getchar(); 14 while(ch <= '9' && ch >= '0')x = x * 10 + ch - '0', ch = getchar(); 15 if(c == '-')x = -x; 16 } 17 18 const int INF = 0x3f3f3f3f; 19 const int MAXN = 100 + 10; 20 const int MAXM = 500 + 10; 21 22 int n,m,cost[MAXN],value[MAXN]; 23 24 struct Edge 25 { 26 int u,v,next; 27 Edge(int _u, int _v, int _next){u = _u;v = _v;next = _next;} 28 Edge(){} 29 }edge[MAXN << 1]; 30 int head[MAXN], cnt; 31 32 inline void insert(int a, int b) 33 { 34 edge[++cnt] = Edge(a, b, head[a]); 35 head[a] = cnt; 36 } 37 38 int b[MAXN],bb[MAXN],low[MAXN],dfn[MAXN],belong[MAXN],group,tot,stack[MAXN],top; 39 40 void tarjan_dfs(int u) 41 { 42 dfn[u] = low[u] = ++tot; 43 b[u] = bb[u] = 1; 44 stack[++top] = u; 45 for(register int pos = head[u];pos;pos = edge[pos].next) 46 { 47 int v = edge[pos].v; 48 if(!b[v]) 49 { 50 tarjan_dfs(v); 51 low[u] = min(low[u], low[v]); 52 } 53 else if(bb[v] && low[u] > dfn[v]) 54 low[u] = dfn[v]; 55 } 56 if(low[u] == dfn[u]) 57 { 58 ++ group; 59 int now = 0; 60 while(now != u) 61 { 62 now = stack[top --]; 63 belong[now] = group; 64 bb[now] = false; 65 } 66 } 67 } 68 69 int cost2[MAXN],value2[MAXN],l[MAXN],r[MAXN],fa2[MAXN]; 70 71 void tarjan() 72 { 73 for(register int i = 1;i <= n;++ i) if(!b[i]) tarjan_dfs(i); 74 for(register int u = 1;u <= n;++ u) 75 { 76 for(register int pos = head[u];pos;pos = edge[pos].next) 77 { 78 int v = edge[pos].v; 79 if(belong[v] != belong[u]) 80 fa2[belong[v]] = belong[u]; 81 } 82 cost2[belong[u]] += cost[u]; 83 value2[belong[u]] += value[u]; 84 } 85 for(register int i = 1;i <= group;++ i) 86 if(fa2[i])r[i] = l[fa2[i]], l[fa2[i]] = i; 87 } 88 89 int dp[MAXN][MAXM],dpb[MAXN]; 90 91 void DP(int u) 92 { 93 if(!u || dpb[u])return; 94 dpb[u] = 1; 95 /* 96 dp[i][j]表示i和i右边的兄弟消耗磁盘空间j的最大价值 97 dp[i][j] = max{ 98 选 f[l[i]][a] + f[r[i]][j - a - cost[i]] + value[i] 99 100 不选 f[r[i]][j] 101 } 102 */ 103 DP(l[u]), DP(r[u]); 104 for(register int j = 0;j <= m;++ j) 105 { 106 for(register int a = 0;a <= m;++ a) 107 { 108 //dp[u][j] = max(dp[u][j], dp[u][j - 1]); 109 if(j - a - cost2[u] >= 0) dp[u][j] = max(dp[u][j], dp[l[u]][a] + dp[r[u]][j - a - cost2[u]] + value2[u]); 110 dp[u][j] = max(dp[u][j], dp[r[u]][j]); 111 } 112 } 113 } 114 115 int main() 116 { 117 read(n), read(m); 118 register int tmp; 119 for(register int i = 1;i <= n;++ i) read(cost[i]); 120 for(register int i = 1;i <= n;++ i) read(value[i]); 121 for(register int i = 1;i <= n;++ i) 122 { 123 read(tmp); 124 if(tmp)insert(tmp, i); 125 } 126 tarjan(); 127 int root = 1; 128 while(!l[root] && root <= group)++ root; 129 if(root <= group) 130 { 131 while(fa2[root])root = fa2[root]; 132 l[group + 1] = root; 133 fa2[root] = group + 1, 134 root = group + 1; 135 ++ group; 136 } 137 else 138 root = group + 1; 139 for(register int i = 1;i <= group;++ i) 140 if(!fa2[i] && i != root) r[i] = l[root], l[root] = i, fa2[i] = root; 141 cost2[root] = value2[root] = 0; 142 DP(root); 143 printf("%d", dp[root][m]); 144 return 0; 145 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号