BZOJ2154 Crash的数字表格

2154: Crash的数字表格

Time Limit: 20 Sec  Memory Limit: 259 MB
Submit: 4315  Solved: 1564
[Submit][Status][Discuss]

Description

今 天的数学课上，Crash小朋友学习了最小公倍数(Least Common Multiple)。对于两个正整数a和b，LCM(a, b)表示能同时被a和b整除的最小正整数。例如，LCM(6, 8) = 24。回到家后，Crash还在想着课上学的东西，为了研究最小公倍数，他画了一张N*M的表格。每个格子里写了一个数字，其中第i行第j列的那个格子里 写着数为LCM(i, j)。一个4*5的表格如下： 1 2 3 4 5 2 2 6 4 10 3 6 3 12 15 4 4 12 4 20 看着这个表格，Crash想到了很多可以思考的问题。不过他最想解决的问题却是一个十分简单的问题：这个表格中所有数的和是多少。当N和M很大 时，Crash就束手无策了，因此他找到了聪明的你用程序帮他解决这个问题。由于最终结果可能会很大，Crash只想知道表格里所有数的和mod 20101009的值。

Input

输入的第一行包含两个正整数，分别表示N和M。

Output

输出一个正整数，表示表格中所有数的和mod 20101009的值。

Sample Input

4 5

Sample Output

122
【数据规模和约定】
100%的数据满足N, M ≤ 10^7。

HINT

Source

 

【题解】

被各种爆

爆爆爆爆

然后modmodmodmod

最后发现对拍的数据超过了题目数据范围

然后发现+1-1写反了一处的弱智错误（明明记得以前没有啊）

然后发现有一个地方的mod离奇失踪了

然后A了

 

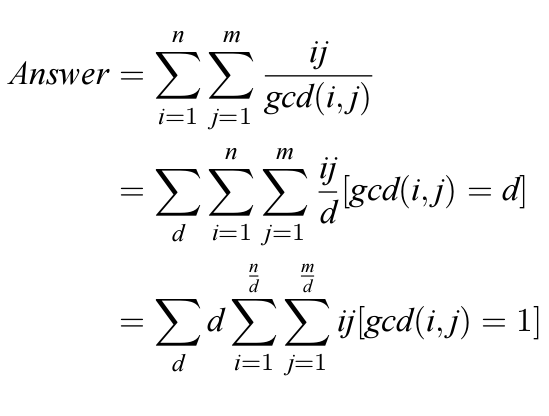
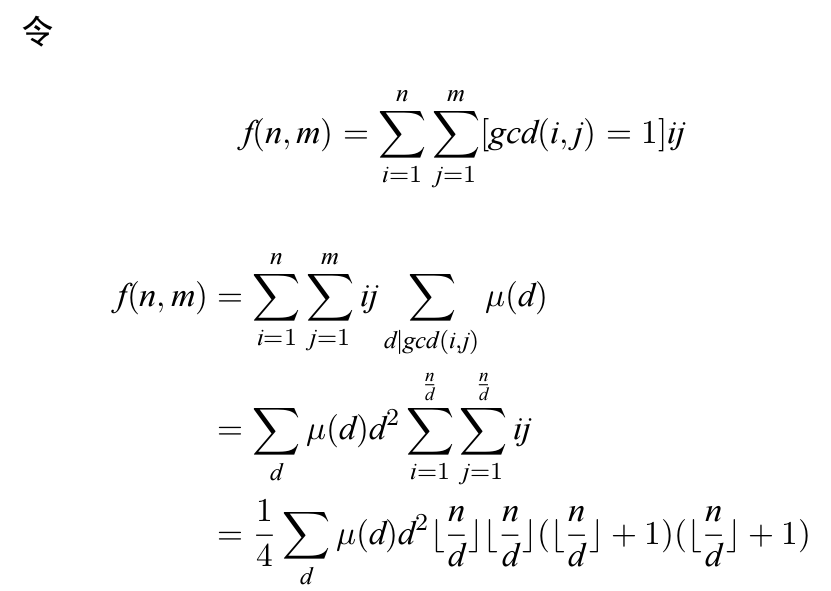
——by mhy12345

 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#define min(a, b) ((a) < (b) ? (a) : (b))
#define max(a, b) ((a) > (b) ? (a) : (b)) 
inline void read(long long &x)
{
    x = 0;char ch = getchar(), c = ch;
    while(ch < '0' || ch > '9')c = ch, ch = getchar();
    while(ch <= '9' && ch >= '0')x = x * 10 + ch - '0', ch = getchar();
    if(c == '-')x = -x;
}
 
const long long INF = 0x3f3f3f3f;
const long long MAXN = 11000000 + 10;
const long long MOD = 20101009;
 
long long n,m,ma,mi,ans,miu[MAXN],bprime[MAXN],prime[MAXN],tot;
 
long long calc(long long n, long long m)
{
    long long re = 0, last, x, y;
    long long mi = min(n, m);
    for(register long long d = 1;d <= mi;++ d)
    {
        x = n/d, y = m/d, last = min(mi, min(n/x, m/y));
        x %= MOD, y %= MOD; 
        re += ((miu[last] - miu[d - 1]) * ((((x * (x + 1)/2)%MOD) * ((y * (y + 1)/2)%MOD))%MOD))%MOD;
        re %= MOD;
        d = last;
    }
    return re%MOD;
}
 
void make_miu()
{
    miu[1] = 1;
    for(register long long i = 2;i <= ma;++ i)
    {
        if(!bprime[i])
        {
            prime[++tot] = i;
            miu[i] = -1;
        }
        for(register long long j = 1;j <= tot && i * prime[j] <= ma;++ j)
        {
            bprime[i * prime[j]] = 1;
            if(i % prime[j] == 0)
            {
                miu[i * prime[j]] = 0;
                break;
            }
            miu[i * prime[j]] = -miu[i];
        }
    }
    for(register long long i = 1;i <= ma;++ i)miu[i] = (miu[i - 1] + (miu[i] * (i * i % MOD))%MOD)%MOD;
}
 
int main()
{
    read(n), read(m);
    mi = min(n, m), ma = max(n,m);
    make_miu();
    long long last, x, y;
    for(register long long d = 1;d <= mi;++ d)
    {
        x = n/d, y = m/d,last = min(mi, min(n/x, m/y));
        x %= MOD, y %= MOD; 
        ans += (calc(x, y)%MOD * (((d + last) * (last - d + 1) / 2)%MOD))%MOD;
        ans %= MOD;
        d = last;
    }
    printf("%lld", (ans + MOD)%MOD); 
    return 0;
}