LeetCode题集-5 - 最长回文子串之马拉车（二）
书接上回，我们今天继续来聊聊最长回文子串的马拉车解法。
题目：给你一个字符串 s，找到 s 中最长的回文子串。
01、中心扩展法优化-合并奇偶处理
俗话说没有最好只有更好，看着O(n^2)的时间复杂度，想想应该还有更优的方案吧，答案是肯定的，马拉车法就可以做到时间和空间复杂度都是O(n)。
其实无论什么算法都是为了解决某种问题而产生的，因此我们还是循序渐进的来优化中心扩展法最终得到马拉车法。
我们知道在中心扩展法中有一个很明显的问题：回文串长度奇偶性需要不同的处理方式，并且在计算之前我们也不知道这个回文串到底是奇还是偶，导致每次我们都需要同时求出奇偶两种情况下的回文串并取最大的那个，因此我们需要首先解决奇偶性导致的差异化处理问题。
如果要解决这个问题可能要从两个方面入手：其一从外部下手找到一个公式统一奇偶性，其二从内部下手修改自身使其变的统一。
关于第一点，因为本题的特点是根据奇偶性做不同的处理，而统一的公式更偏向一个值可以是奇或偶最后得到统一的结果，比如7和8，(7-1)/2=3，(8-1)/2=3，因此第一点并不适合本题。
关于第二点，奇数个字符之间有偶数个空格，偶数个字符之间有奇数个空格，而奇数加偶数还是奇数，也就是如果我们把这些空格考虑进来，奇偶性就统一了，那么接下来还有分析一下这个空格引入后是否会对原回文串特性产生影响，其实并没有影响，对于奇数串相当于中心元素两边各多了一个空格还是对称的，对于偶数相当于中心的两个元素之间加了一个空格结果也还是对称的，因为空格比较特殊，我们选择一个其他特殊符号比如[#]，因此这个方案具有可行。
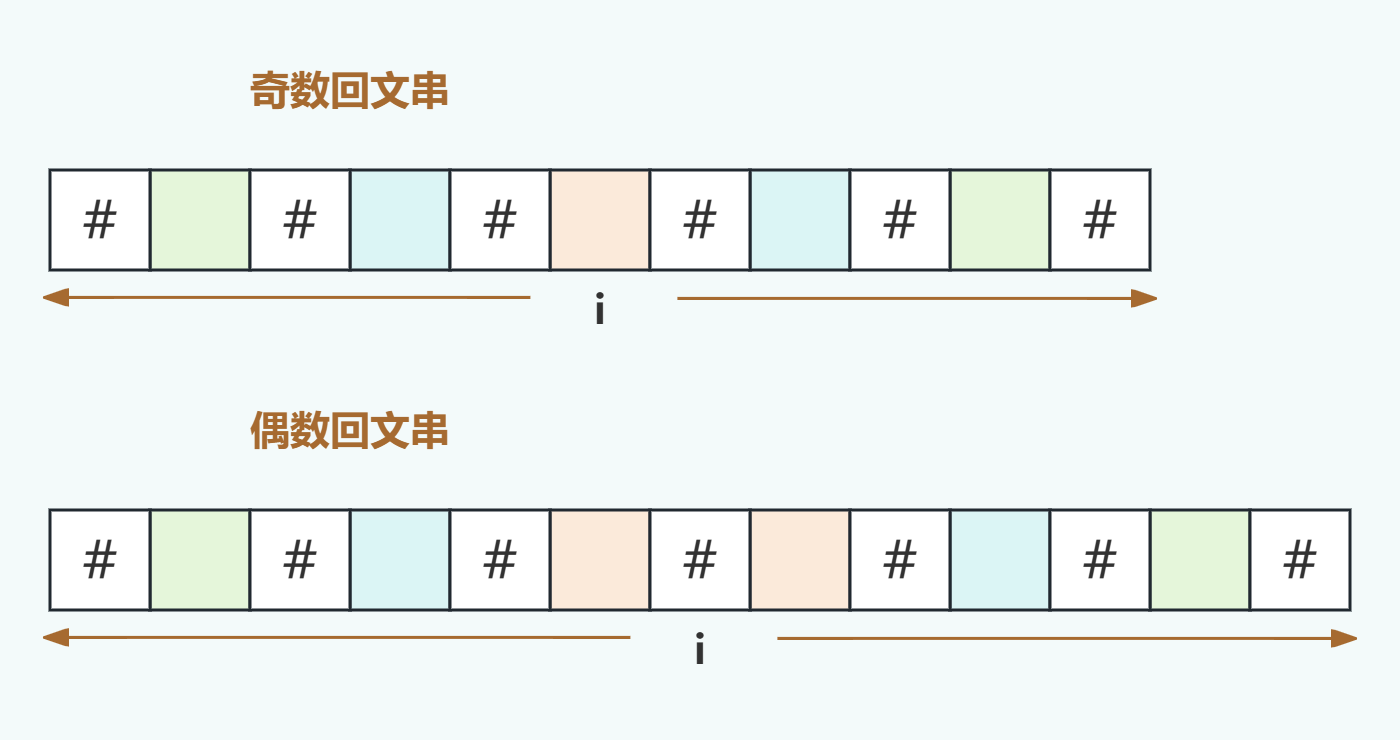
这个方案还有最后一个小问题，就是怎么计算回文串长度，即实现通过处理后的字符串计算出实际的字符长度。
比如上图中原奇数回文串长度是5，处理后长度是11，原偶数回文串长度是6，出来后是13，如果我们不考虑中心元素i，则回文串实际长度正好等于处理后的一半，即原回文串长度=（处理后回文串长度 - 1）/2，我们先给这个值取个名字方便后面交流，叫回文串半径。
到这里优化方案就是确定了，解决了奇偶性问题，解决了字符串处理后转换问题，下面我们看看具体实现代码。
//中心扩散法-合并奇偶
public static string CenterExpandMergeOddEven(string s)
{
//如果字符串为空或只有一个字符，直接返回该字符串
if (s == null || s.Length < 1)
{
return "";
}
// 预处理字符串，插入#字符以统一处理奇偶回文串
//比如：s="cabac"转化为s="#c#a#b#a#c#"
var tmp = $"#{string.Join("#", s.ToCharArray())}#";
//记录最长回文子串的起始位置和最大长度
var startIndex = 0;
var maxLength = 0;
//从左到右遍历处理过的字符串，求每个字符的回文串半径
for (var i = 0; i < tmp.Length; ++i)
{
//计算当前以i为中心的回文串半径
var radius = PalindromicRadius(tmp, i, i);
//如果当前计算的半径大于maxLength，就更新startIndex
if (radius > maxLength)
{
startIndex = (i - radius) / 2;
maxLength = radius;
}
}
//根据startIndex和maxLength，从原始字符串中截取返回
return s.Substring(startIndex, maxLength);
}
//回文串半径
public static int PalindromicRadius(string s, int leftIndex, int rightIndex)
{
//左边界大于等于首字符，右边界小于等于尾字符，并且左右字符相等
while (leftIndex >= 0 && rightIndex < s.Length && s[leftIndex] == s[rightIndex])
{
//从中心往两端扩展一位
//向左扩展
--leftIndex;
//向右扩展
++rightIndex;
}
//返回回文串半径（注意本来应该是（rightIndex - leftIndex + 1）/2，
//但是满足条件后leftIndex、rightIndex又分别向左和右又各扩展了一位，
//因此需要把这两位减掉，因为中心元素不在计算返回还需要减掉一位，
//因此（rightIndex - leftIndex + 1 - 2 - 1）/2
//所以最后公式为（rightIndex - leftIndex - 1）/2）
return (rightIndex - leftIndex - 2) / 2;
}
时间复杂度：O(n2)，由于每遍到一个字符，都需要往左/右进行探测，所以是O(n2)。
空间复杂度：O(1)。
因此这次优化性能上并没有任何提升，只是处理方式上做了优化，这一步并不是白做，而是为了下面马拉车法做前期准备。
02、中心扩展法再优化（马拉车法）
再暴力破解法优化中我们用到了经典的以空间换时间的做法，把已经计算过的子字符串结果存储下来减少了不必要的计算，同样的我也可以用类似的思想来优化中心扩展法。
暴力破解法用了回文串对称性由外向内判断是否是回文串，中心扩展法用了回文串对称性由内向外判断是否是回文串，而这两种方法都是应用了对称性去算，那么我们能否直接用回文串的对称性直接判断是否为回文串呢？答案是肯定的，下面我们用图例来说明其中原理。
在上面的合并奇偶处理中，我们知道处理后回文串半径长度就是我们最终回文串长度。如果我们把已经计算过的回文串半径存储下来，后面需要的时候就可以直接拿过来用了。
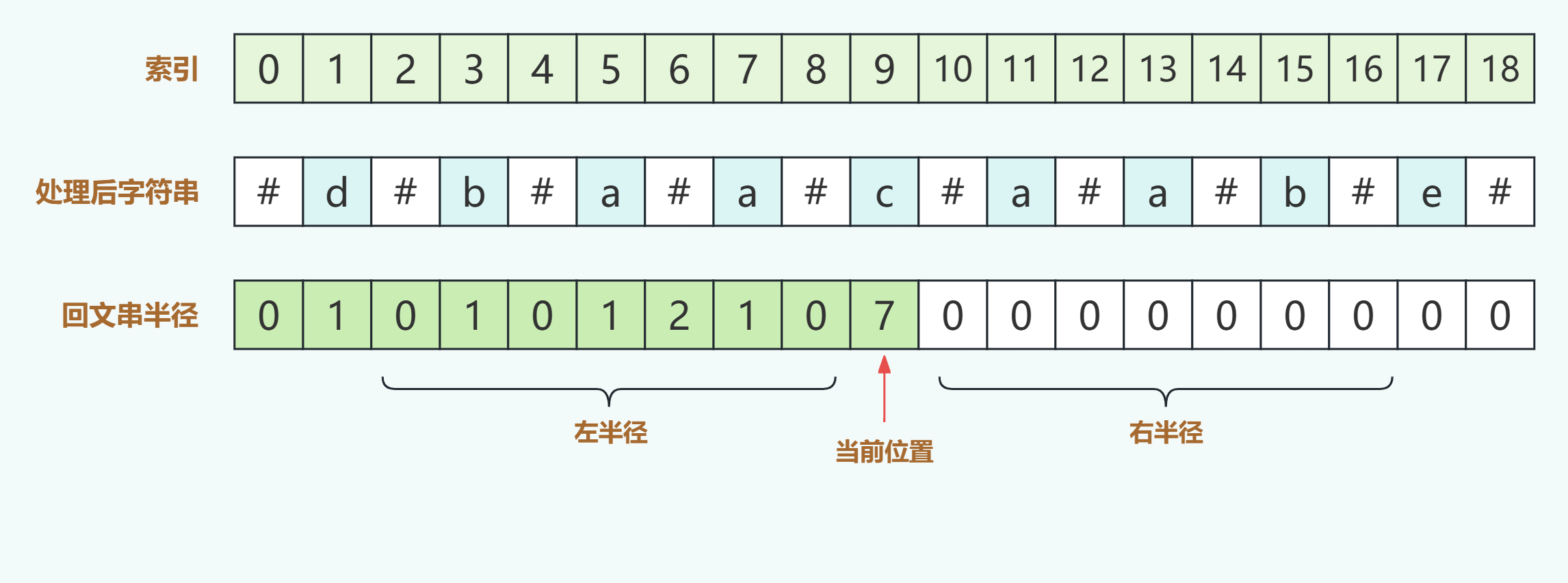
如上图，在回文串半径行中，绿色背景表示已经计算完回文串半径的字符，并中心扩展是从左往右计算的，此时计算完了s[9]即字符c处，那么我们想象一下此时如何计算索引为10即s[10]元素的回文串半径呢？s[11]、s[12]呢？
回想一下上文提到的对称性，如果我们以当前位置s[9]为中心点，那么其右半径和其左半径是对称的，也就是说相对应的元素应该是性质相同的，可以合理猜测s[10]应该和s[8]的回文串半径一致也为0，同理猜测s[11]=s[7]=1，s[12]=s[6]=2。
当然这并不绝对，我们只是想拿来说明我们可以利用对称性，把其对称点已经计算过的结果利用上，虽然上面的s[10]，s[11]，s[12]三个值是对的，但描述并不准确，因为存在s[10]>s[8]的情况。如下图：
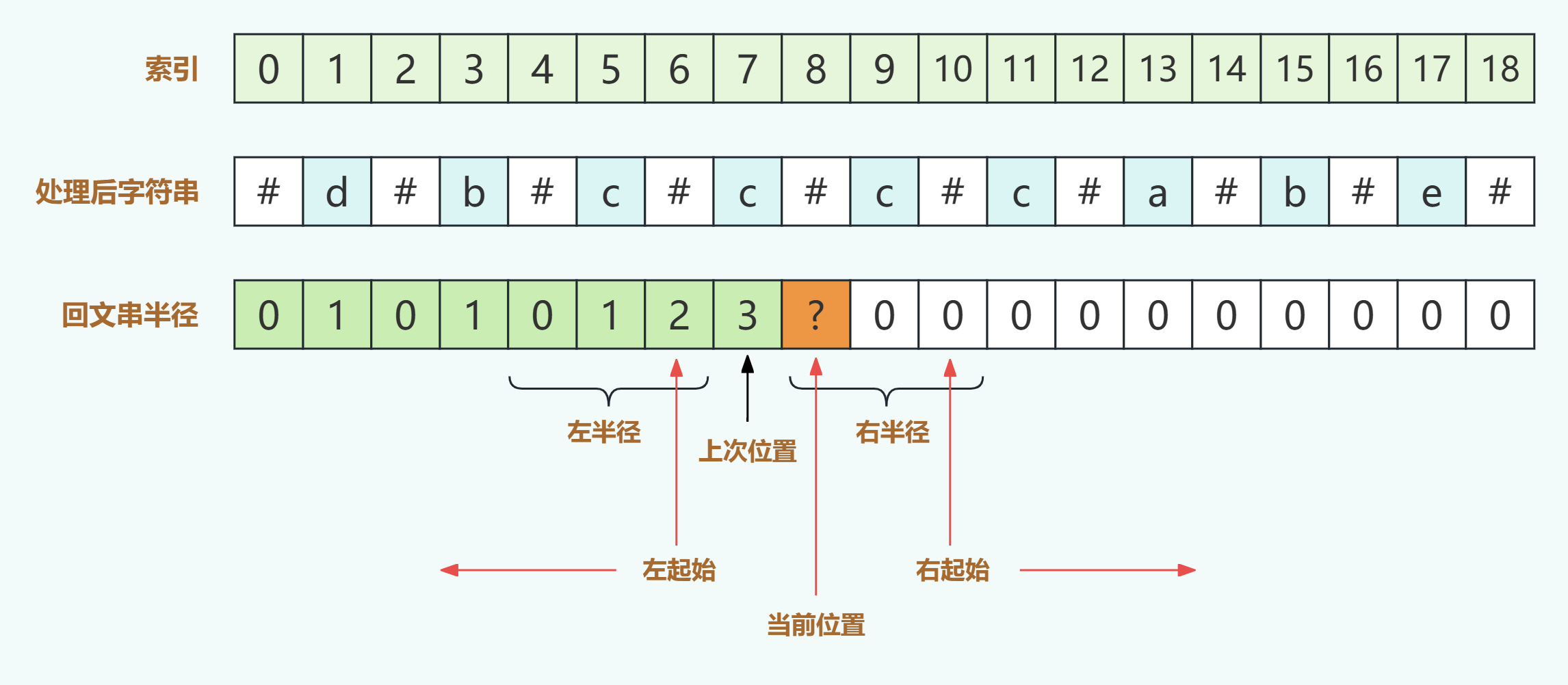
如上图，当上一次处理完s[7]，可得其回文串半径为3，此时开始计算s[8],使用对称性可得s[8]>=s[6],因此我们在计算以s[8]为中心向两边扩展查找回文串时不需要再以s[8]为起点了，而是根据s[6]=2,我们直接跳跃2位，左边从s[6],右边从s[10],开始向两边扩展查找以s[8]为中心的实际回文串长度，最后计算可能为4，这一步正是整个算法的核心所在。
因此我们可以把这个算法分为两种情况：
（1）当前位置大于当前已探测右侧最远位置，则直接使用中心扩展方法查找回文串；
（2）当前位置小于等于当前已探测右侧最远位置，则根据其对称位置已计算结果，进行直接选择跳过部分位再开始使用中心扩展方法查找回文串；
当然起始位置、已探测最右侧位置、中心点、最大长度怎么选，什么时候更新，跳过多少位后再计算，这些都是细节部分了，我们下面直接看代码。
//马拉车法
public static string Manacher(string s)
{
if (s == null || s.Length == 0)
{
return "";
}
var tmp = $"#{string.Join("#", s.ToCharArray())}#";
//rightIndex表示目前计算出的最右端范围，rightIndex和左边都是已探测过的
var rightIndex = 0;
//centerIndex最右端位置的中心对称点
var centerIndex = 0;
//记录最长回文子串的起始位置和最大长度
var startIndex = 0;
var maxLength = 0;
//radiusPoints数组记录所有已探测过的回文串半径，后面我们再计算i时，根据radiusPoints[iMirror]计算i
var radiusPoints = new int[tmp.Length];
//从左到右遍历处理过的字符串，求每个字符的回文串半径
for (var i = 0; i < tmp.Length; i++)
{
//根据i和right的位置分为两种情况：
//1、i<=right利用已知的信息来计算i
//2、i>right，说明i的位置时未探测过的，只能用中心探测法
if (i <= rightIndex)
{
// 找出i关于前面中心的对称
var iMirror = 2 * centerIndex - i;
//这句是关键，不用再像中心探测那样，一点点的往左/右扩散，
//根据已知信息减少不必要的探测，必须选择两者中的较小者作为左右探测起点
var minRadiusLength = Math.Min(rightIndex - i, radiusPoints[iMirror]);
//这里左右-1和+1是因为对称性可以直接跳过相应的回文串半径
radiusPoints[i] = PalindromicRadius(tmp, i - minRadiusLength - 1, i + minRadiusLength + 1);
}
else
{
//i落在rightIndex右边，是没被探测过的，只能用中心探测法
//这里左右-1和+1，是因为中心点字符肯定是回文串，可以直接跳过
radiusPoints[i] = PalindromicRadius(tmp, i - 1, i + 1);
}
//大于rightIndex，说明可以更新最右端范围了，同时更新centerIndex
if (i + radiusPoints[i] > rightIndex)
{
centerIndex = i;
rightIndex = i + radiusPoints[i];
}
//找到了一个更长的回文半径，更新原始字符串的startIndex位置
if (radiusPoints[i] > maxLength)
{
startIndex = (i - radiusPoints[i]) / 2;
maxLength = radiusPoints[i];
}
}
//根据start和maxLen，从原始字符串中截取一段返回
return s.Substring(startIndex, maxLength);
}
//回文串半径
public static int PalindromicRadius(string s, int leftIndex, int rightIndex)
{
//左边界大于等于首字符，右边界小于等于尾字符，并且左右字符相等
while (leftIndex >= 0 && rightIndex < s.Length && s[leftIndex] == s[rightIndex])
{
//从中心往两端扩展一位
//向左扩展
--leftIndex;
//向右扩展
++rightIndex;
}
//返回回文串半径（注意本来应该是（rightIndex - leftIndex + 1）/2，
//但是满足条件后leftIndex、rightIndex又分别向左和右又各扩展了一位，
//因此需要把这两位减掉，因为中心元素不在计算返回还需要减掉一位，
//因此（rightIndex - leftIndex + 1 - 2 - 1）/2
//所以最后公式为（rightIndex - leftIndex - 1）/2）
return (rightIndex - leftIndex - 2) / 2;
}
时间复杂度：O(n)，可能比较难以理解的是为什么for嵌套了while还是O(n)的时间复杂度？因为首先每个字符最多只会进行一次扩展，其次当进行一次新的扩展后，当前位置到最新的有边界这部分可以通过对称性得到而不需要再次扩展，因此while总的操作次数不会大于n，再加上预处理字符串n，以及初始化的辅助数组2n+1，因此整体还是O(n)。
空间复杂度：O(n)，我们需要 O(n) 的空间记录每个位置的半径。
这就是马拉车算法的整个过程，我们再来总结一下，马拉车算法是对中心扩展法的优化，解决了其两个问题：其一奇偶统一处理，其二利用对称性减少重复计算。其中第二点的重点是通过对称性不用每次扩展都从中心点出发，而是直接跳过已计算的部分位。
注：测试方法代码以及示例源码都已经上传至代码库，有兴趣的可以看看。https://gitee.com/hugogoos/Planner
