数据结构 - 散列表,再探
书接上回,我们继续来聊散列表。
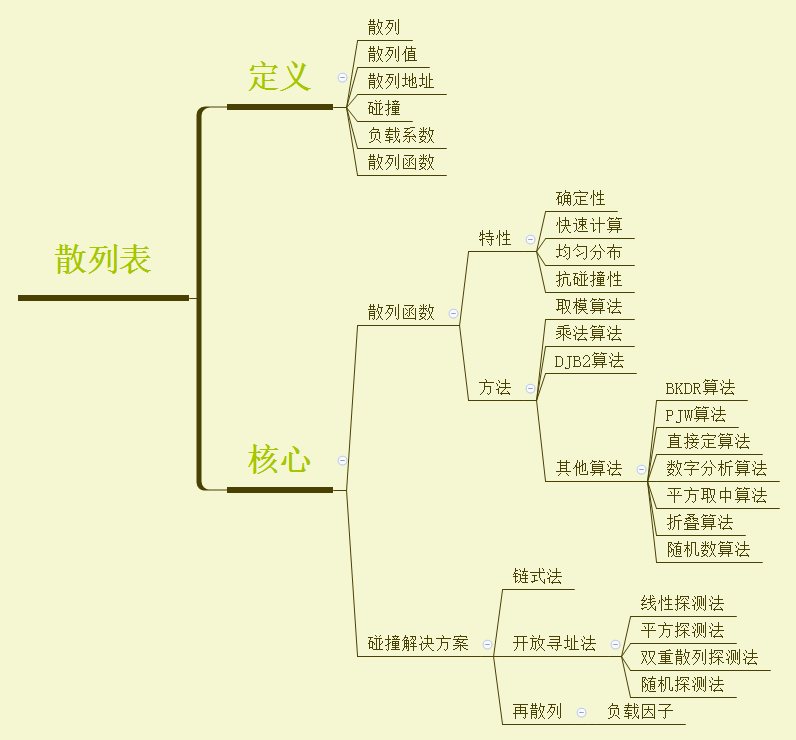
从上面的章节不难发现,无论散列函数怎么构建总会发生碰撞,最多只能降低碰撞概率,但是并不能杜绝碰撞,因此如何解决碰撞问题成了散列重中之重。
01、碰撞解决方案
下面我们一起来看看几种碰撞处理策略。
1、链式法
链式法的核心思想可以理解为把碰撞的key直接放到一个大的集合中;
我们先来回顾一下何为碰撞,碰撞就是两个不同的key,通过散列函数计算出相同的散列值。
为什么发生碰撞就会出问题呢?因为散列表本质上是数组,数组一个下标只能对应一个值,如果key1和key2发生碰撞,意味着key2对应的value2会把key1对应的value1覆盖掉,这就会导致了数据丢失。
想解决这个问题我直观想法是如果发生碰撞时value2不是覆盖value1,而是两者同时存储下来,是不是这个问题就解决了呢?
答案是肯定的,但是里面还有很多细节要处理。如一个数组元素里怎么再存放多个元素呢?对于发生碰撞的key如何查找呢?
首先一个数组元素里怎么存放多个元素?其实方法有很多,比如数组元素中直接存放一个数组,比如数组中存放一个链表表头指向一个链表等等。
在散列表中,每个数组元素所在的位置,我们称为“ 桶” 或者 “ 槽”,而每个桶(槽)又对应一条链表,发生碰撞的所有key都放到相同的桶对应的链表中,这种碰撞处理策略称为链式法。
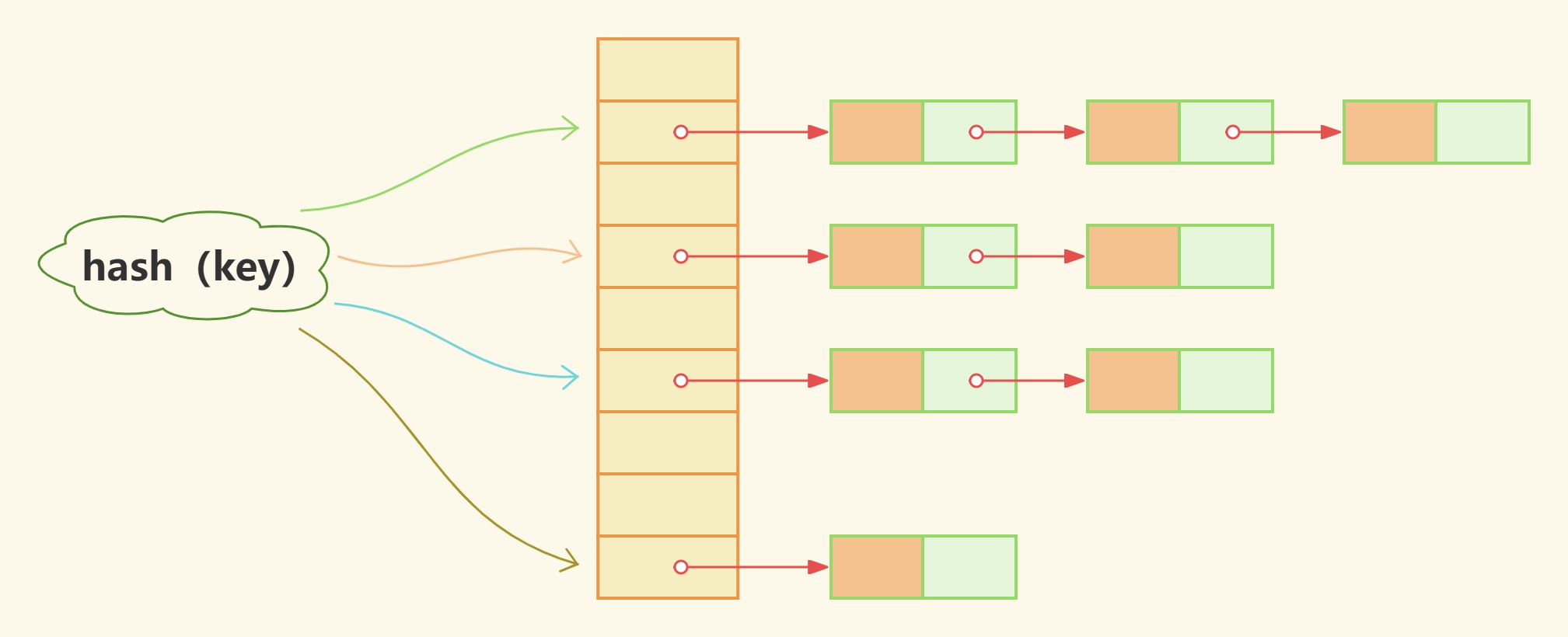
当存取元素时分两步,第一步先找到key所在的桶,第二步再在桶所对应的链表中存取元素。
这个方案是非常简单实用的,而且因为链表节点是动态申请这也大大提升了空间利用率。
2、开放寻址法
开放寻址法的核心思想可以理解为当发生冲突时,如果当前散列位置已被使用就按某种方式继续探测下一个可以用的散列位置。
而某种方式继续探测具体是指当发生冲突时,则在当前散列值基础上再加上指定的步长并判断当前散列位置是否可用,如果不可用则重复此步骤。
因此开放寻址法可以概况为:hash_value=(hash(key)+step(i))%m,1≤i≤m-1
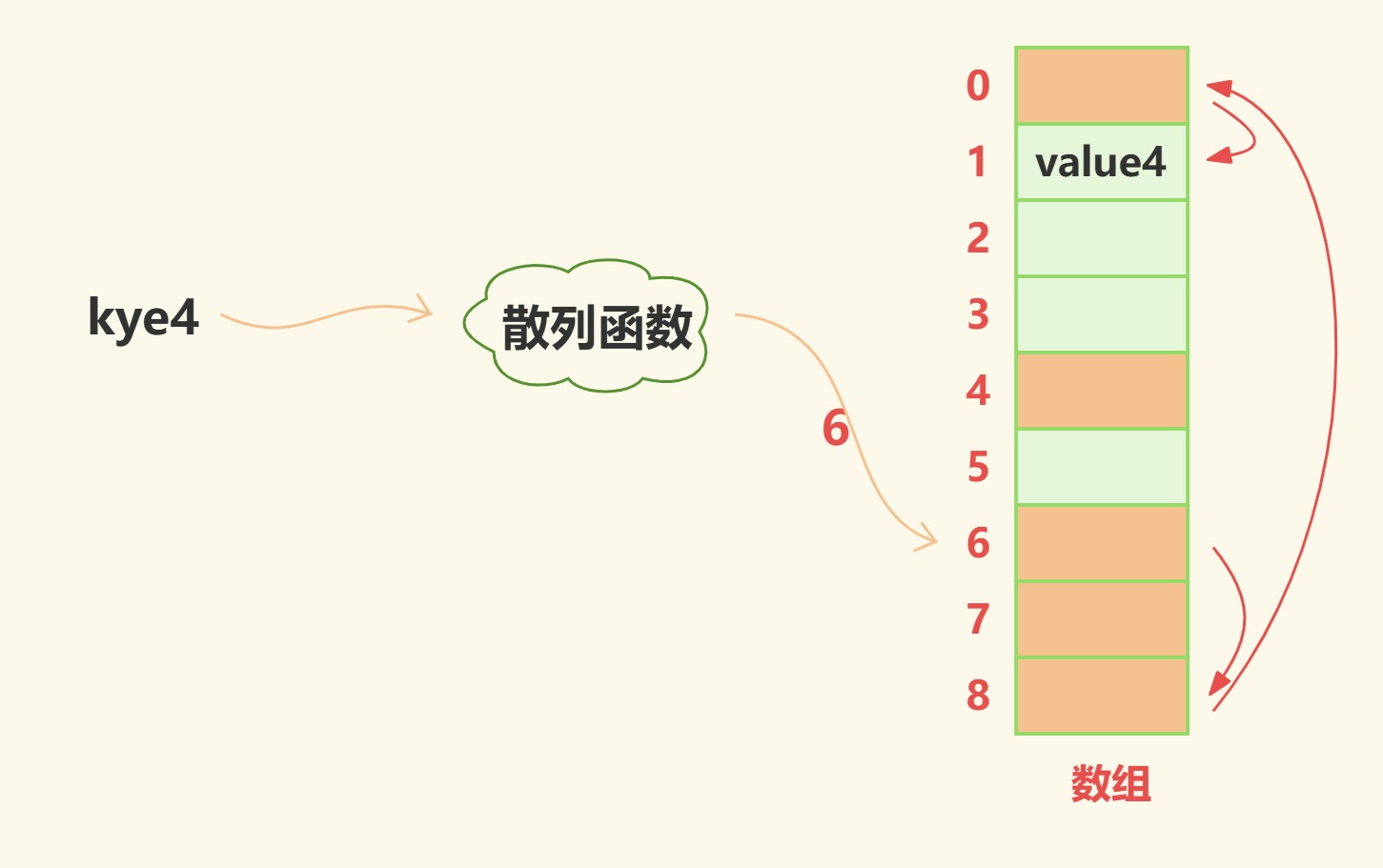
如上图当如果数组中浅绿代表空地址,浅橙色表示已经被占用,当传入key4时,经过散列函数计算出所在数组索引应该为6,而此时索引6已经被占用,因此继续往后探测,索引8已经被占用,继续往后探测,索引0已经被占用,继续往后探测,索引1空闲,存入value4。
而根据不同的步长生成规则,又可以分成以下几种探测方法:线性探测法、平方探测法、双重散列探测法、随机探测法等等
(1)线性探测法
线性探测法是通过在散列表中线性探测下一个可用位置来解决碰撞。
当发生碰撞时,则按顺序探测下一个元素位置,直至查找到可用的散列地址或者排查完全表。因此当探查到表尾地址时,并不是结束探测而是回到表首继续探测,直至探测到起始探测位置。
其公式可表示为:hash_value=(hash(key)+step)%m,1≤step≤m-1
优点:1、实现简单;2、效率较高,在负载因子较低时特别更为突出。
缺点:可能导致聚集现象,即多个元素在碰撞后会集中在一起,从而导致相邻位置被占用,增加探测时间。
(2)平方探测法
平方探测法是通过使用平方增量来解决哈希冲突,从而有效地分散元素。
如果说线性探测法每次探测的步长是step,那么平方探测法的探测步长则是step的平方。
其公式可表示为:hash_value=(hash(key)+step^2)%m,1≤step≤m-1
与线性探测法相比,平方探测法主要优势在于增量平方数使得探测位置分布更广,位置也就更分散,从而减少元素的聚焦现象,从而提高查找效率。因此平方探测法在处理碰撞时通常优于线性探测法,当然选择哪种方法应根据具体应用场景和性能要求来决定。
优点:减少聚集现象,元素分布均匀。
缺点:1、仍可能存在二次聚集现象(即某些位置可能因为探测规则而频繁被访问)。2、可能无法探测到所有位置,在负载因子较高时尤为突出。
(3)双重散列探测法
双重散列探测法是使用两个散列函数来决定探测序列,从而更有效地分散冲突。也就是当发生碰撞时,会使用第二个散列函数来生成增量从而确定下一个要查找的位置。
其公式可表示为:hash_value=(hash(key)+ i * hash2(key))%m,1≤i≤m-1
优点:1、减少聚集现象,效率高,探测路径较为随机。2、可以探测到所有位置,理论上避免了聚集问题。
缺点:实现相对复杂,且需要选择合适的第二个散列函数。
(4)随机探测法
随机探测法是通过随机选择下一个探测位置来解决冲突。也就是说当发生碰撞时,确定查找的下一个位置的增量式一个随机数。
其公式可表示为:hash_value=(hash(key)+ r)%m,1≤r≤m-1
优点:1、大幅减少聚集现象,位置探测随机性强。2可以有效分散元素,降低碰撞影响。
缺点:1、随机性可能导致性能不稳定,尤其是在负载因子较高时。2、难以预测和调试。
总结
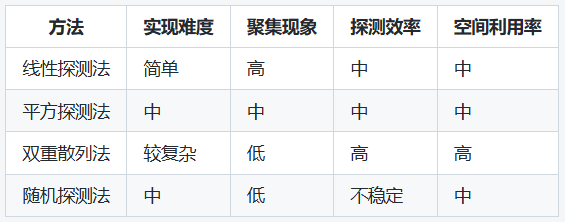
3、再散列法
再散列法的核心思想可用理解为对现有散列表进行扩容并重新计算现有元素位置。
我们先来回忆一个概念负载因子,负载因子式用来衡量散列表填充程度,通过散列表已存储的元素个数除以散列表的大小计算可得。
负载因子过大会导致一些列问题,首先会加大碰撞概率,碰撞概率增大又会导致处理碰撞成本增加,进而导致性能下降。同时也可能导致内存碎片化使用率不高,等等问题。
而负载因子就是触发再散列的时机,当负载因子超过某个阈值(一般是0.75)时,进行再散列。
而再散列的难点在于如何处理新老数据,是当触发再散列时一次性迁移所有老数据到新散列表中,还是分批次迁移老数据直至所有老数据迁移完成为止?
一次性迁移可能实现上相对简单,但是也引发了很多问题,如果迁移过程中又有其他操作怎么办?如果数据量很大迁移时间过长怎么办?
而分批迁移实现上会更复杂一些,要处理好新老数据共存时的查找、插入、删除等操作。
整体思路如下:
(1)当负载因子到达设定的阈值,则重新申请新的内存空间,不进行老数据迁移;
(2)当有新数据要插入时,将新数据插入至新的内存空间中,并取出一个老数据插入到新的内存空间中;
(3)重复步骤(2)直至所有老数据都迁移至新的内存空间为止;
(4)当在新老数据共存进行查找时,可用先在老的空间进行查找,如果不存在再到新空间中查找。
注:测试方法代码以及示例源码都已经上传至代码库,有兴趣的可以看看。https://gitee.com/hugogoos/Planner





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 一个费力不讨好的项目,让我损失了近一半的绩效!
· 清华大学推出第四讲使用 DeepSeek + DeepResearch 让科研像聊天一样简单!
· 实操Deepseek接入个人知识库
· CSnakes vs Python.NET:高效嵌入与灵活互通的跨语言方案对比
· Plotly.NET 一个为 .NET 打造的强大开源交互式图表库