opencv-12-高斯滤波-双边滤波(附C++代码实现)

开始之前

这几天由于自己的原因没有写, 一个是因为自己懒了, 一个是感觉这里遇到点问题不想往下写了, 我们先努力结束这个章节吧, 之前介绍了比较常用而且比较好理解的均值和中值滤波, 但是呢,在例程Smoothing Images, 还有给出的其他的滤波方式, 主要是高斯滤波和双边滤波,

我们这一次完结掉滤波与平滑的这个部分, 写的有点多了,反而不想再写了, 加油

目录

本文目标

本文主要是介绍

  • 高斯滤波
  • 双边滤波

和之前介绍的一样, 我们仍然还是 介绍一下原理, 给出一下具体的形式, 然后使用 opencv 进行一下实现的过程, 最后使用我们之前的图像进行测试 进行算法的分析与总结.

正文

高斯滤波(Gaussian Filter)

我们在之前介绍了中值滤波是统计排序的结果, 属于非线性的结果, 均值滤波是使用模板核进行的操作, 我们在的文章中也提到了均值滤波在计算的过程中必须要考虑权重的问题, 进而提出了加权的均值滤波的操作, 比如最常见的加权均值滤波的操作核.

\[M = \frac{1}{16} \left [ \begin{array}{c} 1 & 2 & 1 \\ 2& 4 & 2 \\ 1 & 2 & 1 \end{array} \right ] \]

其实呢,这个核也就是高斯滤波器在 3*3窗口的离散取整的结果值, 最明显的特点就是模板的系数随着距离模板中心的距离而变换, 能够有效的抑制噪声,平滑图像, 相比均值滤波能够更好的平滑图像, 保留图像边缘.

高斯滤波原理

由于我们的图像是二维的, 但是高斯分布是一维的, 那我们先考虑一维的高斯分布, 就是我们常用的正太分布曲线,

\[G(x) = \frac{1}{\sqrt{2\pi \sigma}} e^{-\frac{x^2}{2\sigma^2}} \]

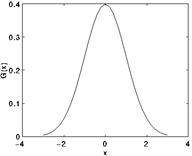
一维高斯分布

对于二维的高斯分布其实可以考虑成两个方向的运算相叠加的得到的结果

\[G(x,y) = \frac{1}{2\pi \sigma^2} e^{-\frac{x^2+y^2}{2\sigma^2}} = G(x)*G(y) \]

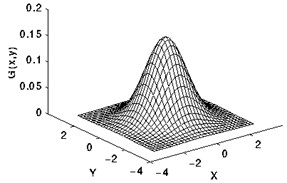
二维高斯分布

考虑到图像的计算实际上是离散的座标, 对于窗口大小为 \((2k + 1) \times (2k + 1)\) 模板, 我们可以表示成

\[G{i,j} = \frac{1}{2\pi \sigma ^ 2}e ^{-\frac{(i - k - 1)^2 + (j - k - 1)^2}{2 \sigma ^ 2}} \]

可以参考图像处理基础(4)：高斯滤波器详解
里面给出的方法, 使用

void generateGaussianTemplate(double window[][11], int ksize, double sigma)
{
    static const double pi = 3.1415926;
    int center = ksize / 2; // 模板的中心位置，也就是坐标的原点
    double x2, y2;
    for (int i = 0; i < ksize; i++)
    {
        x2 = pow(i - center, 2);
        for (int j = 0; j < ksize; j++)
        {
            y2 = pow(j - center, 2);
            double g = exp(-(x2 + y2) / (2 * sigma * sigma));
            g /= 2 * pi * sigma*sigma;	// 
            window[i][j] = g;
        }
    }
    double k = 1 / window[0][0]; // 将左上角的系数归一化为1
    for (int i = 0; i < ksize; i++)
    {
        for (int j = 0; j < ksize; j++)
        {
            window[i][j] *= k;
        }
    }
}

生成了\(3 \times 3, \sigma = 0.8\) 的高斯模板, 对应的将其取整就得到了

\[M = \frac{1}{16} \left [ \begin{array}{c} 1 & 2 & 1 \\ 2& 4 & 2 \\ 1 & 2 & 1 \end{array} \right ] \]

上面给出的文章同样的详细介绍了 \(\sigma\) 在统计学中的意义, 可以去参考学习
不过根据高中的知识, 我们可以看到 正态分布的曲线

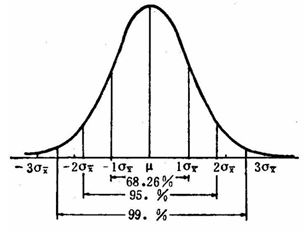
正态分布曲线

C++ 实现

在我们之前提到的图像处理基础(4)：高斯滤波器详解 这里给出了基于 opencv 的代码实现, 这里是\(O(m*n*k^2)\) 的算法实现

// 来源链接: https://www.cnblogs.com/wangguchangqing/p/6407717.html
void GaussianFilter(const Mat &src, Mat &dst, int ksize, double sigma)
{
    CV_Assert(src.channels() || src.channels() == 3); // 只处理单通道或者三通道图像
    const static double pi = 3.1415926;
    // 根据窗口大小和sigma生成高斯滤波器模板
    // 申请一个二维数组，存放生成的高斯模板矩阵
    double **templateMatrix = new double*[ksize];
    for (int i = 0; i < ksize; i++)
        templateMatrix[i] = new double[ksize];
    int origin = ksize / 2; // 以模板的中心为原点
    double x2, y2;
    double sum = 0;
    for (int i = 0; i < ksize; i++)
    {
        x2 = pow(i - origin, 2);
        for (int j = 0; j < ksize; j++)
        {
            y2 = pow(j - origin, 2);
            // 高斯函数前的常数可以不用计算，会在归一化的过程中给消去
            double g = exp(-(x2 + y2) / (2 * sigma * sigma));
            sum += g;
            templateMatrix[i][j] = g;
        }
    }
    for (int i = 0; i < ksize; i++)
    {
        for (int j = 0; j < ksize; j++)
        {
            templateMatrix[i][j] /= sum;
            cout << templateMatrix[i][j] << " ";
        }
        cout << endl;
    }
    // 将模板应用到图像中
    int border = ksize / 2;
    copyMakeBorder(src, dst, border, border, border, border, BorderTypes::BORDER_REFLECT);
    int channels = dst.channels();
    int rows = dst.rows - border;
    int cols = dst.cols - border;
    for (int i = border; i < rows; i++)
    {
        for (int j = border; j < cols; j++)
        {
            double sum[3] = { 0 };
            for (int a = -border; a <= border; a++)
            {
                for (int b = -border; b <= border; b++)
                {
                    if (channels == 1)
                    {
                        sum[0] += templateMatrix[border + a][border + b] * dst.at<uchar>(i + a, j + b);
                    }
                    else if (channels == 3)
                    {
                        Vec3b rgb = dst.at<Vec3b>(i + a, j + b);
                        auto k = templateMatrix[border + a][border + b];
                        sum[0] += k * rgb[0];
                        sum[1] += k * rgb[1];
                        sum[2] += k * rgb[2];
                    }
                }
            }
            for (int k = 0; k < channels; k++)
            {
                if (sum[k] < 0)
                    sum[k] = 0;
                else if (sum[k] > 255)
                    sum[k] = 255;
            }
            if (channels == 1)
                dst.at<uchar>(i, j) = static_cast<uchar>(sum[0]);
            else if (channels == 3)
            {
                Vec3b rgb = { static_cast<uchar>(sum[0]), static_cast<uchar>(sum[1]), static_cast<uchar>(sum[2]) };
                dst.at<Vec3b>(i, j) = rgb;
            }
        }
    }
    // 释放模板数组
    for (int i = 0; i < ksize; i++)
        delete[] templateMatrix[i];
    delete[] templateMatrix;
}

然后同样的给出了分离的实现, 将图像进行水平运算之后再进行竖直运算, 计算的时间上会有一定的速度提升

// 来源链接: https://www.cnblogs.com/wangguchangqing/p/6407717.html
// 分离的计算
void separateGaussianFilter(const Mat &src, Mat &dst, int ksize, double sigma)
{
    CV_Assert(src.channels()==1 || src.channels() == 3); // 只处理单通道或者三通道图像
    // 生成一维的高斯滤波模板
    double *matrix = new double[ksize];
    double sum = 0;
    int origin = ksize / 2;
    for (int i = 0; i < ksize; i++)
    {
        // 高斯函数前的常数可以不用计算，会在归一化的过程中给消去
        double g = exp(-(i - origin) * (i - origin) / (2 * sigma * sigma));
        sum += g;
        matrix[i] = g;
    }
    // 归一化
    for (int i = 0; i < ksize; i++)
        matrix[i] /= sum;
    // 将模板应用到图像中
    int border = ksize / 2;
    copyMakeBorder(src, dst, border, border, border, border, BorderTypes::BORDER_REFLECT);
    int channels = dst.channels();
    int rows = dst.rows - border;
    int cols = dst.cols - border;
    // 水平方向
    for (int i = border; i < rows; i++)
    {
        for (int j = border; j < cols; j++)
        {
            double sum[3] = { 0 };
            for (int k = -border; k <= border; k++)
            {
                if (channels == 1)
                {
                    sum[0] += matrix[border + k] * dst.at<uchar>(i, j + k); // 行不变，列变化；先做水平方向的卷积
                }
                else if (channels == 3)
                {
                    Vec3b rgb = dst.at<Vec3b>(i, j + k);
                    sum[0] += matrix[border + k] * rgb[0];
                    sum[1] += matrix[border + k] * rgb[1];
                    sum[2] += matrix[border + k] * rgb[2];
                }
            }
            for (int k = 0; k < channels; k++)
            {
                if (sum[k] < 0)
                    sum[k] = 0;
                else if (sum[k] > 255)
                    sum[k] = 255;
            }
            if (channels == 1)
                dst.at<uchar>(i, j) = static_cast<uchar>(sum[0]);
            else if (channels == 3)
            {
                Vec3b rgb = { static_cast<uchar>(sum[0]), static_cast<uchar>(sum[1]), static_cast<uchar>(sum[2]) };
                dst.at<Vec3b>(i, j) = rgb;
            }
        }
    }
    // 竖直方向
    for (int i = border; i < rows; i++)
    {
        for (int j = border; j < cols; j++)
        {
            double sum[3] = { 0 };
            for (int k = -border; k <= border; k++)
            {
                if (channels == 1)
                {
                    sum[0] += matrix[border + k] * dst.at<uchar>(i + k, j); // 列不变，行变化；竖直方向的卷积
                }
                else if (channels == 3)
                {
                    Vec3b rgb = dst.at<Vec3b>(i + k, j);
                    sum[0] += matrix[border + k] * rgb[0];
                    sum[1] += matrix[border + k] * rgb[1];
                    sum[2] += matrix[border + k] * rgb[2];
                }
            }
            for (int k = 0; k < channels; k++)
            {
                if (sum[k] < 0)
                    sum[k] = 0;
                else if (sum[k] > 255)
                    sum[k] = 255;
            }
            if (channels == 1)
                dst.at<uchar>(i, j) = static_cast<uchar>(sum[0]);
            else if (channels == 3)
            {
                Vec3b rgb = { static_cast<uchar>(sum[0]), static_cast<uchar>(sum[1]), static_cast<uchar>(sum[2]) };
                dst.at<Vec3b>(i, j) = rgb;
            }
        }
    }
    delete[] matrix;
}

这里的算法都是 上面提到的https://www.cnblogs.com/wangguchangqing/p/6407717.html 这篇文章, 具体可以去看内容

opencv 高斯滤波

其实这篇文章图像处理--高斯滤波写的很好
其实主要的结构也就是他给出的过程

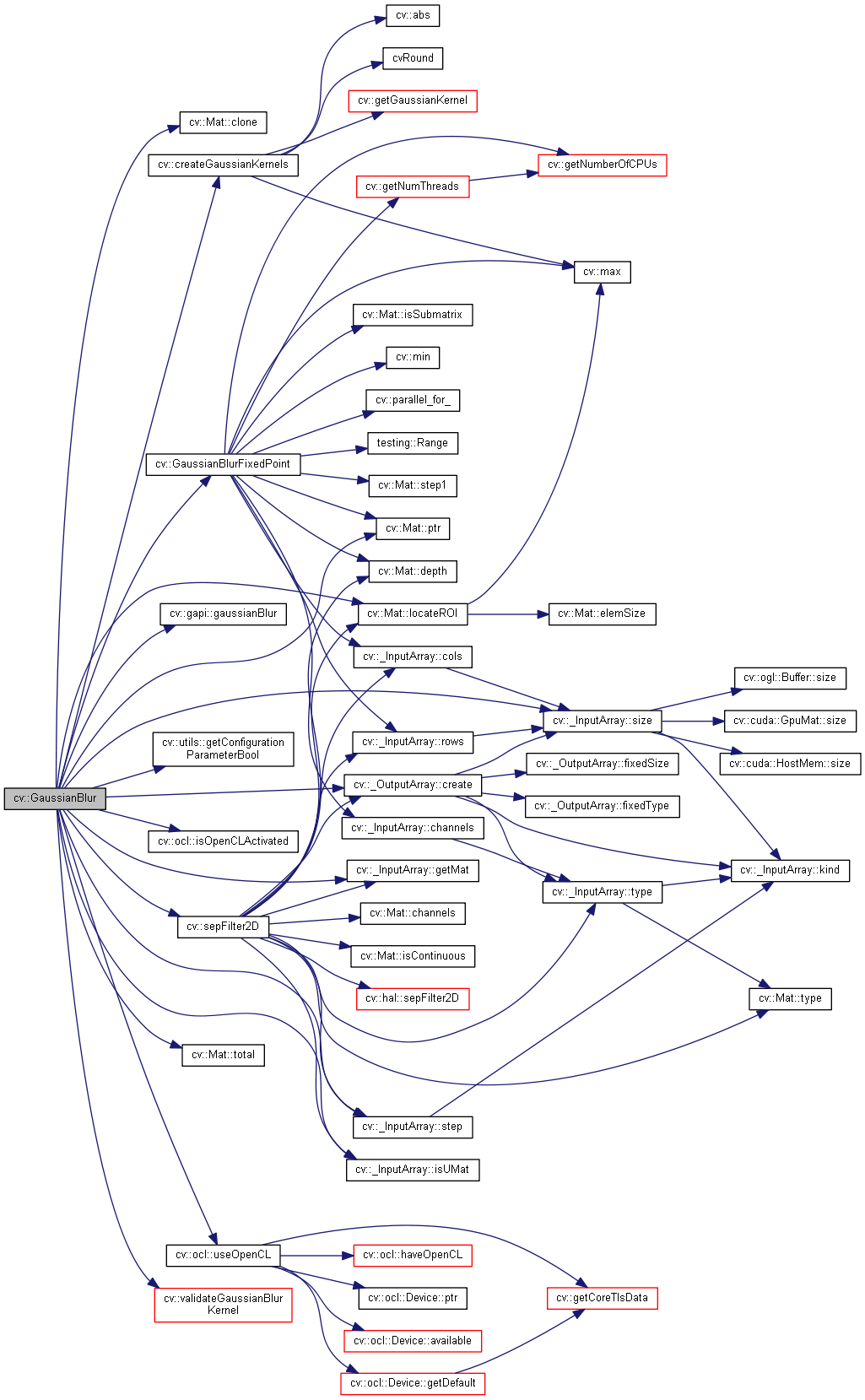
高斯函数调用图

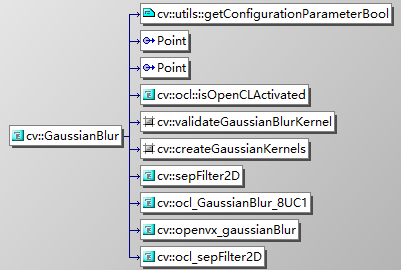
高斯滤波函数调用简图

其实整个高斯滤波的过程就是创建高斯核, 然后使用 filter2D 的方法进行的滤波操作, 具体要深入的话可以看函数的调用图, 实现起来也是一样的思路, 很简单的操作, 我们之后测试一下效果..

// /modules\imgproc\src\smooth.dispatch.cpp:600
void GaussianBlur(InputArray _src, OutputArray _dst, Size ksize,
                  double sigma1, double sigma2,
                  int borderType)
  • src ‪输入图像
  • dst 输出图像
  • ksize 核的尺寸 奇数
  • sigmaX x 方向 的 sigma 值
  • sigmaY ‪y 方向 的 sigma 值
  • borderType 边界处理的方式

高斯滤波效果对比

我们还是使用之前的高椒盐噪声图像, 然后直接进行算法滤波, 计算结果就好, 跟之前的测试图像很相似, 这里

测试结果图

这里的四张图分别对应 高噪声图像, 直接高斯滤波的结果, 分离xy方向进行滤波结果,以及opencv 自带的高斯滤波效果图, 这里是预览图像, 实际的检测结果就是上面给出的参数值, 实际上效果只能说一般, 我们之后再进行算法层面的对比.

image-noise: psnr:19.4727, mssim: B:0.353134 G:0.383638 R:0.629353
image-noise: psnr:26.3155, mssim: B:0.584585 G:0.617172 R:0.812303
image-noise: psnr:26.1721, mssim: B:0.574719 G:0.607494 R:0.809844
image-noise: psnr:26.4206, mssim: B:0.598176 G:0.630657 R:0.819658

双边滤波(Bilateral Filter)

双边滤波原理

我们在上面提出了高斯滤波的原理是对于距离模板中心 距离不同给予不同的权重, 而双边滤波则不仅考虑图像的空间距离, 还要考虑其灰度距离, 对于越接近中间灰度值的点权重越高, 灰度值相差大的则权重更小.

双边滤波的原理可以参考双边滤波（Bilateral Filter）详解,
可以参考Bilateral Filtering for Gray and Color Images

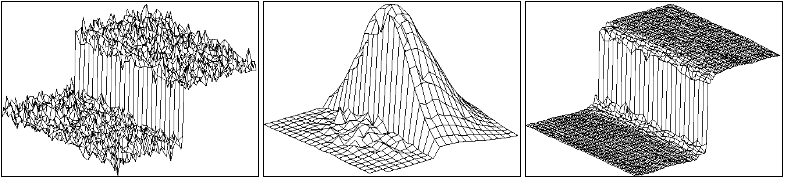
双边滤波原理

在文章图像处理基础(5)：双边滤波器详细介绍了双边滤波
其实跟上面给出的滤波演示一致, 都是在保证图像边缘信息的情况下进行噪声的滤波..

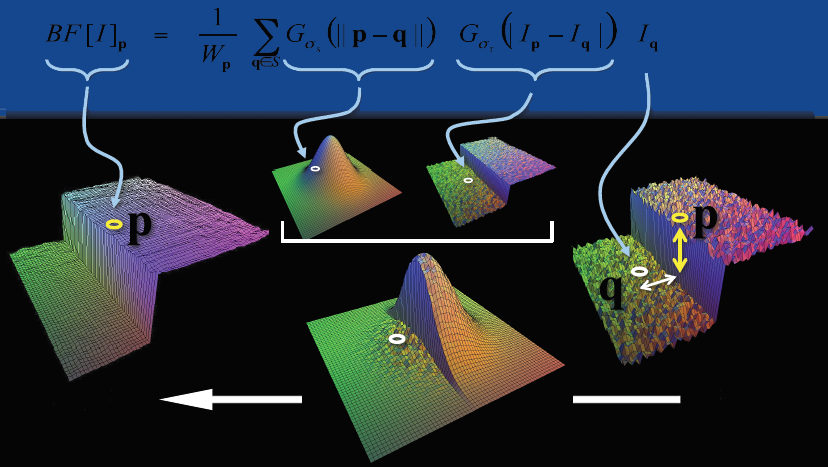
双边滤波原理

可以参考bilateral filter双边滤波器的通俗理解 给出的双边滤波的数学表达

\[g(x,y) = \frac{\sum_{kl}f(k,l)w(i,j,k,l)}{\sum_{kl}w(i,j,k,l)} \]

对于不同的模板系数又有两个部分, 主要是 空间域模板权值 \(w_d\) 和 灰度域 模板权值 \(w_r\),

\[\begin{array}{rl} w_d(i,j,k,l) &= e^{-\frac{(i-k)^2 +(j-l)^2}{2\sigma_d^2}} \\ w_r(i,j,k,l) &= e^{-\frac{\left \| f(i,j) - f(k,l) \right \|} {2\sigma_r^2}} \\ w &= w_d * w_r \end{array} \]

其中，\(q(i,j)\) 为模板窗口的其他系数的坐标，\(f(i,j)\) 表示图像在点\(q(i,j)\) 处的像素值；\(p(k,l)\) 为模板窗口的中心坐标点，对应的像素值为\(f(k,l)\) ；\(\sigma_r\) 为高斯函数的标准差。

C++ 实现 双边滤波

感觉这里写的挺好的 图像处理基础(5)：双边滤波器, 手动实现了双边滤波, 我们可以详细的参考, 这里

// 参考来源: https://www.cnblogs.com/wangguchangqing/p/6416401.html
void myBilateralFilter(const Mat &src, Mat &dst, int ksize, double space_sigma, double color_sigma)
{
    int channels = src.channels();
    CV_Assert(channels == 1 || channels == 3);
    double space_coeff = -0.5 / (space_sigma * space_sigma);
    double color_coeff = -0.5 / (color_sigma * color_sigma);
    int radius = ksize / 2;
    Mat temp;
    copyMakeBorder(src, temp, radius, radius, radius, radius, BorderTypes::BORDER_REFLECT);
    vector<double> _color_weight(channels * 256); // 存放差值的平方
    vector<double> _space_weight(ksize * ksize); // 空间模板系数
    vector<int> _space_ofs(ksize * ksize); // 模板窗口的坐标
    double *color_weight = &_color_weight[0];
    double *space_weight = &_space_weight[0];
    int    *space_ofs = &_space_ofs[0];
    for (int i = 0; i < channels * 256; i++)
        color_weight[i] = exp(i * i * color_coeff);
    // 生成空间模板
    int maxk = 0;
    for (int i = -radius; i <= radius; i++)
    {
        for (int j = -radius; j <= radius; j++)
        {
            double r = sqrt(i*i + j * j);
            if (r > radius)
                continue;
            space_weight[maxk] = exp(r * r * space_coeff); // 存放模板系数
            space_ofs[maxk++] = i * temp.step + j * channels; // 存放模板的位置，和模板系数相对应
        }
    }
    // 滤波过程
    for (int i = 0; i < src.rows; i++)
    {
        const uchar *sptr = temp.data + (i + radius) * temp.step + radius * channels;
        uchar *dptr = dst.data + i * dst.step;
        if (channels == 1)
        {
            for (int j = 0; j < src.cols; j++)
            {
                double sum = 0, wsum = 0;
                int val0 = sptr[j]; // 模板中心位置的像素
                for (int k = 0; k < maxk; k++)
                {
                    int val = sptr[j + space_ofs[k]];
                    double w = space_weight[k] * color_weight[abs(val - val0)]; // 模板系数 = 空间系数 * 灰度值系数
                    sum += val * w;
                    wsum += w;
                }
                dptr[j] = (uchar)cvRound(sum / wsum);
            }
        }
        else if (channels == 3)
        {
            for (int j = 0; j < src.cols * 3; j+=3)
            {
                double sum_b = 0, sum_g = 0, sum_r = 0, wsum = 0;
                int b0 = sptr[j];
                int g0 = sptr[j + 1];
                int r0 = sptr[j + 2];
                for (int k = 0; k < maxk; k++)
                {
                    const uchar *sptr_k = sptr + j + space_ofs[k];
                    int b = sptr_k[0];
                    int g = sptr_k[1];
                    int r = sptr_k[2];
                    double w = space_weight[k] * color_weight[abs(b - b0) + abs(g - g0) + abs(r - r0)];
                    sum_b += b * w;
                    sum_g += g * w;
                    sum_r += r * w;
                    wsum += w;
                }
                wsum = 1.0f / wsum;
                b0 = cvRound(sum_b * wsum);
                g0 = cvRound(sum_g * wsum);
                r0 = cvRound(sum_r * wsum);
                dptr[j] = (uchar)b0;
                dptr[j + 1] = (uchar)g0;
                dptr[j + 2] = (uchar)r0;
            }
        }
    }
}

opencv 实现 双边滤波

void bilateralFilter( InputArray _src, OutputArray _dst, int d,
                      double sigmaColor, double sigmaSpace,
                      int borderType )
  • InputArray src: 输入图像，可以是Mat类型，图像必须是8位或浮点型单通道、三通道的图像。
  • OutputArray dst: 输出图像，和原图像有相同的尺寸和类型。
  • int d: 表示在过滤过程中每个像素邻域的直径范围。如果这个值是非正数，则函数会从第五个参数sigmaSpace计算该值。
  • double sigmaColor: 颜色空间过滤器的sigma值，这个参数的值月大，表明该像素邻域内有越宽广的颜色会被混合到一起，产生较大的半相等颜色区域。 （这个参数可以理解为值域核的）
  • double sigmaSpace: 坐标空间中滤波器的sigma值，如果该值较大，则意味着越远的像素将相互影响，从而使更大的区域中足够相似的颜色获取相同的颜色。当d>0时，d指定了邻域大小且与sigmaSpace无关，否则d正比于sigmaSpace. （这个参数可以理解为空间域核的）
  • int borderType=BORDER_DEFAULT: 用于推断图像外部像素的某种边界模式，有默认值BORDER_DEFAULT.

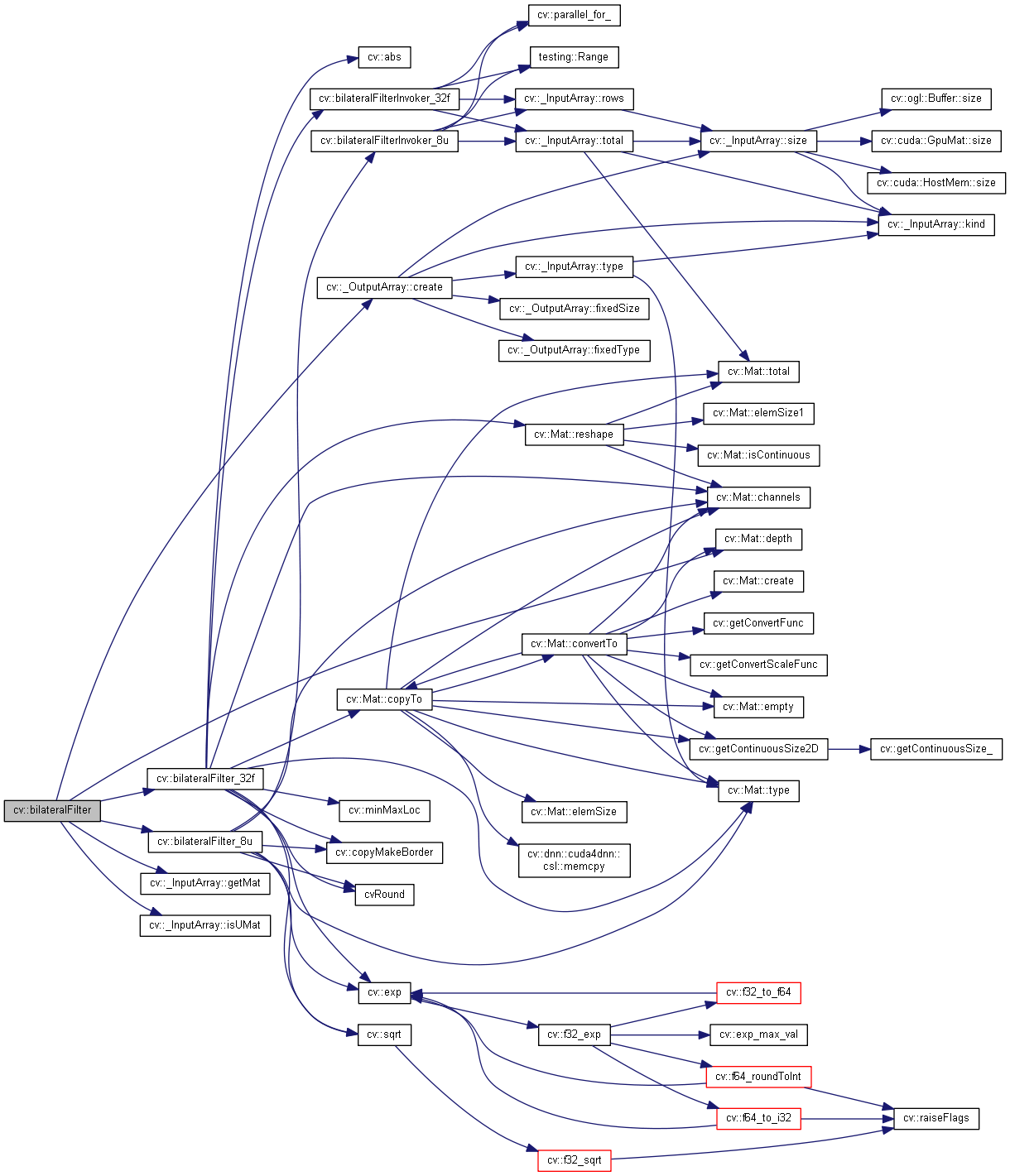
双边滤波函数调用图

双边滤波算法对比

一开始的时候看双边滤波真的搞不懂, 也不知道这么做有什么目的, 最终的结果又代表什么, 我们按照之前的方法去测试我们的图像, 结果真的是几种算法中最差的了, 但是这只是说不适用于我们的图像结果, 在实际使用过程中还是要进行测试之后才能得出结论

测试结果如下: 对应原始图和 手动实现的结果以及 opencv 的结果 都使用的 是3 的窗口, sigma 的值 为 255
, 这篇文章https://blog.csdn.net/Jfuck/article/details/8932978 讲的很好, 介绍了参数对滤波的影响, 可以学习一下..

image-noise: psnr:19.4727, mssim: B:0.353134 G:0.383638 R:0.629353
image-noise: psnr:24.4502, mssim: B:0.538774 G:0.570666 R:0.776195
image-noise: psnr:24.4691, mssim: B:0.539177 G:0.571087 R:0.776461

双边滤波算法

总结

其实个人使用双边滤波真的不算很多, 在之前研究导向滤波的时候才了解过很多, 这里写的比较差吧, 只能说勉强能看, 强烈推荐 https://www.cnblogs.com/wangguchangqing/category/740760.html 这个系列, 将的很详细, 很多都是博文里面的内容, 可以参考学习, 高斯滤波就比较简单了, 其实复杂的滤波过程主要是理解算法, 然后根据算法的思路进行代码的实现过程, 最后做一定的程序上的优化就好, 理解第一, 实现其次.. 希望带给读者一点点启发..

我这里一开始不准备写这么多的, 结果越写越多, 导致自己收不住了, 很多自己说不上很了解的地方, 这一次也是深入的了解了一下, 但是还是很僵硬, 只能说能用而已, 这里还是推荐看我给出的链接或者自己去查阅相关的内容, 我这里只是给出一个大略的介绍, 如果有错误还请指名, 十分感谢

参考链接

  1. 《快速高斯滤波、高斯模糊、高斯平滑(二维卷积分步为一维卷积)_人工智能_青城山小和尚-CSDN博客》. 见于 2020年5月10日. https://blog.csdn.net/qq_36359022/article/details/80188873.
  2. 《双边滤波 - 旗亭涉的博客 | Qitingshe Blog》. 见于 2020年5月10日. https://qitingshe.github.io/2018/06/14/双边滤波/.
  3. 《双边滤波（Bilateral Filter）详解_人工智能_Jfuck的专栏-CSDN博客》. 见于 2020年5月10日. https://blog.csdn.net/Jfuck/article/details/8932978.
  4. 《雙邊濾波器》. 收入 维基百科，自由的百科全书, 2019年11月16日. https://zh.wikipedia.org/w/index.php?title=雙邊濾波器&oldid=56898678.
  5. 《图像处理--高斯滤波_网络_L-inYi的专栏-CSDN博客》. 见于 2020年5月10日. https://blog.csdn.net/L_inYi/article/details/8915116.
  6. 《图像处理基础(4)：高斯滤波器详解 - Brook_icv - 博客园》. 见于 2020年5月10日. https://www.cnblogs.com/wangguchangqing/p/6407717.html.
  7. 《图像处理基础(5)：双边滤波器 - Brook_icv - 博客园》. 见于 2020年5月10日. https://www.cnblogs.com/wangguchangqing/p/6416401.html.
  8. 《图像处理－线性滤波－3 高斯滤波器 - Tony Ma - 博客园》. 见于 2020年5月10日. https://www.cnblogs.com/pegasus/archive/2011/05/20/2052031.html.
  9. 《【转】高斯图像滤波原理及其编程离散化实现方法_Smile_Gogo_新浪博客》. 见于 2020年5月10日. http://blog.sina.com.cn/s/blog_640577ed0100yz8v.html.
  10. 《bilateral filter双边滤波器的通俗理解_网络_pan_jinquan的博客-CSDN博客》. 见于 2020年5月10日. https://blog.csdn.net/guyuealian/article/details/82660826.
  11. 《Bilateral Filtering》. 见于 2020年5月10日. http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/MANDUCHI1/Bilateral_Filtering.html.
  12. 《Cv图像处理 - OpenCV China ：图像处理,计算机视觉库,Image Processing, Computer Vision》. 见于 2020年5月10日. http://wiki.opencv.org.cn/index.php/Cv图像处理.
  13. 《o(1)复杂度之双边滤波算法的原理、流程、实现及效果。 - 云+社区 - 腾讯云》. 见于 2020年5月10日. https://cloud.tencent.com/developer/article/1011738.

本文由博客一文多发平台 OpenWrite 发布！

posted @ 2020-05-10 16:52  SChen1024  阅读(4277)  评论(0)  编辑  收藏  举报