交叉熵损失函数的优点(转载)
附加内容:透彻理解熵(包括信息熵和交叉熵)
一文搞懂交叉熵在机器学习中的使用,透彻理解交叉熵背后的直觉
第一篇:
利用一些饱和激活函数的如sigmoid激活时,假如利用均方误差损失,那么损失函数向最后一层的权重传递梯度时,梯度公式为
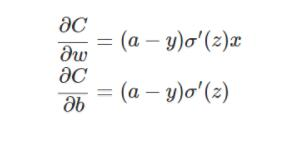
可见梯度与最后一层的激活函数的导数成正比,因此,如果起始输出值比较大,也即激活函数的导数比较小,那么整个梯度幅度更新幅度都比较小,收敛时间很长。若一开始输出值比较小那么更新速度比较好,收敛也快,因此不稳定。且与输出值a与真实值的误差成正比。
再看损失函数改成交叉熵损失时:

此时损失函数对于最后一层权重的梯度不再跟激活函数的导数相关,只跟输出值和真实值的差值成正比,此时收敛较快。又反向传播是连乘的,因此整个权重矩阵的更新都会加快。
另外,多分类交叉熵损失求导更简单,损失仅与正确类别的概率有关。而且损失对于softmax激活层的输入求导很简单。

————————————————
版权声明:本文为CSDN博主「无它,唯手熟尔」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_42422981/article/details/90645074
另外一篇:
一.前言
在做神经网络的训练学习过程中,一开始,经常是喜欢用二次代价函数来做损失函数,因为比较通俗易懂,后面在大部分的项目实践中却很少用到二次代价函数作为损失函数,而是用交叉熵作为损失函数。为什么?一直在思考这个问题,这两者有什么区别,那个更好?下面通过数学的角度来解释下。
思考:
1.我们希望我们损失函数能够做到,当我们预测的值跟目标值越远时,在修改参数时候,减去一个更大的值,做到更加快速的下降。
2.哪个函数更不容易陷入局部最优解
二.两种代价函数的表达式
二次代价损失函数:
交叉熵损失函数:
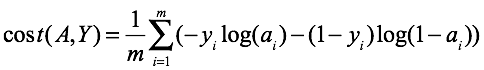
针对二分类来说,其中:
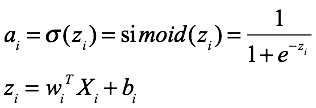
ai第Xi个样本经过前向传播之后到达最后一个节点的值
三.收敛速度比较
两个函数反向传播梯度比较
1.二次代价函数
为了方便只取一个样本,那么损失为:

那么w,b的梯度为:
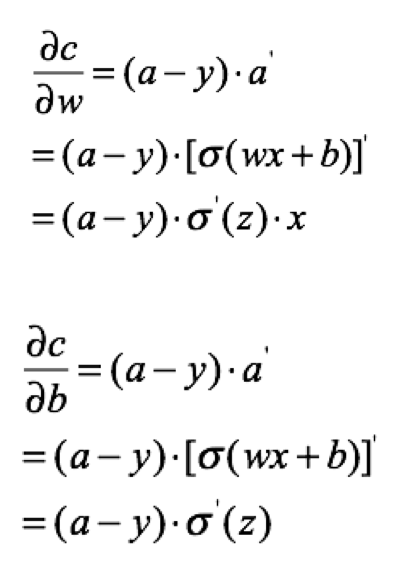
2.交叉熵
为了方便只取一个样本,损失为:
计算w,b的梯度:

分析和结论
由此可看出,在做后向传播时
1.对于square mean在更新w,b时候,w,b的梯度跟激活函数的梯度成正比,激活函数梯度越大,w,b调整就越快,训练收敛就越快,但是Simoid函数在值非常高时候,梯度是很小的,比较平缓。
2.对于cross entropy在更新w,b时候,w,b的梯度跟激活函数的梯度没有关系了,bz已经表抵消掉了,其中bz-y表示的是预测值跟实际值差距,如果差距越大,那么w,b调整就越快,收敛就越快。
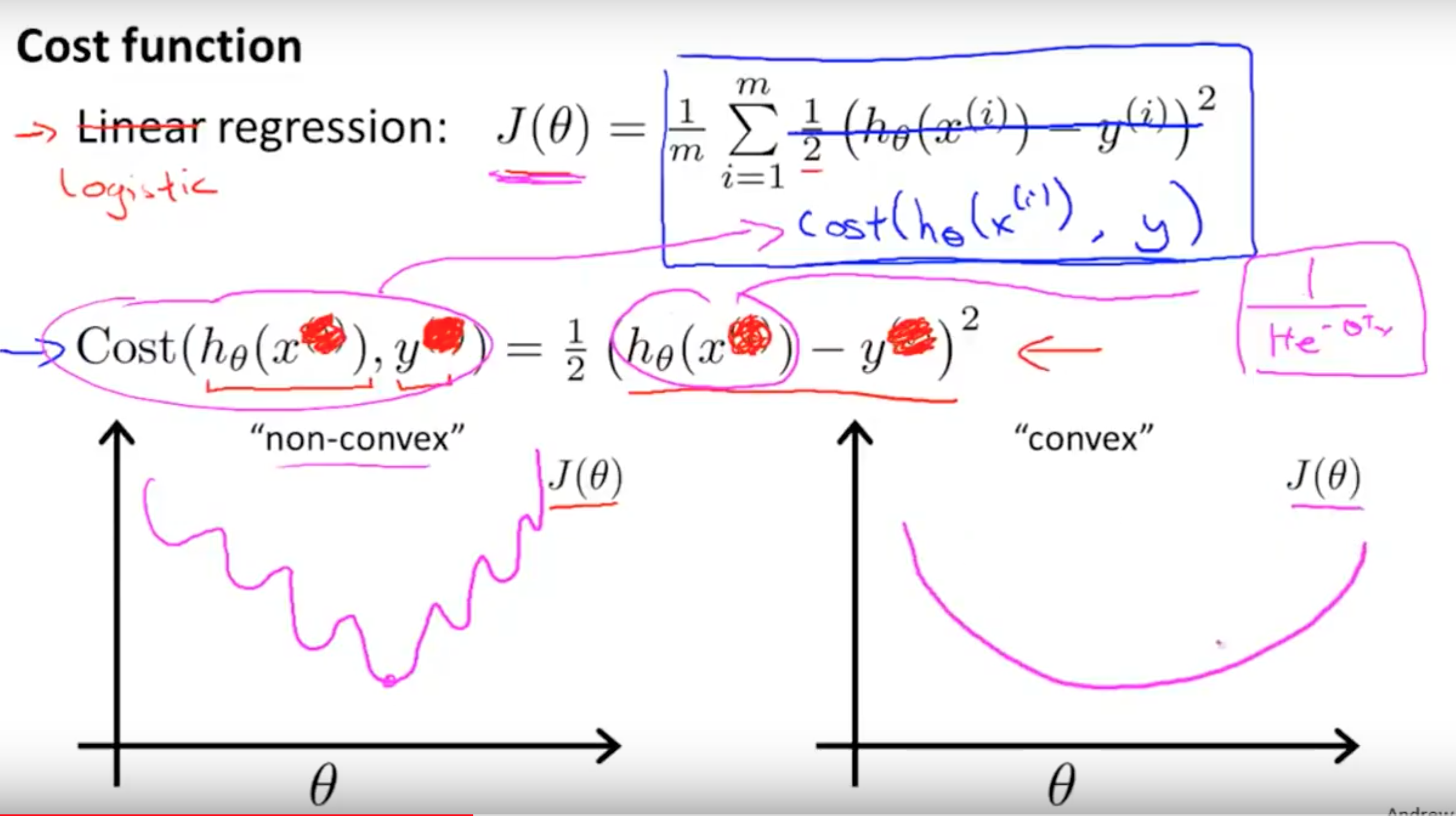
四.两个损失函数的函数图像
square mean:
交叉熵:
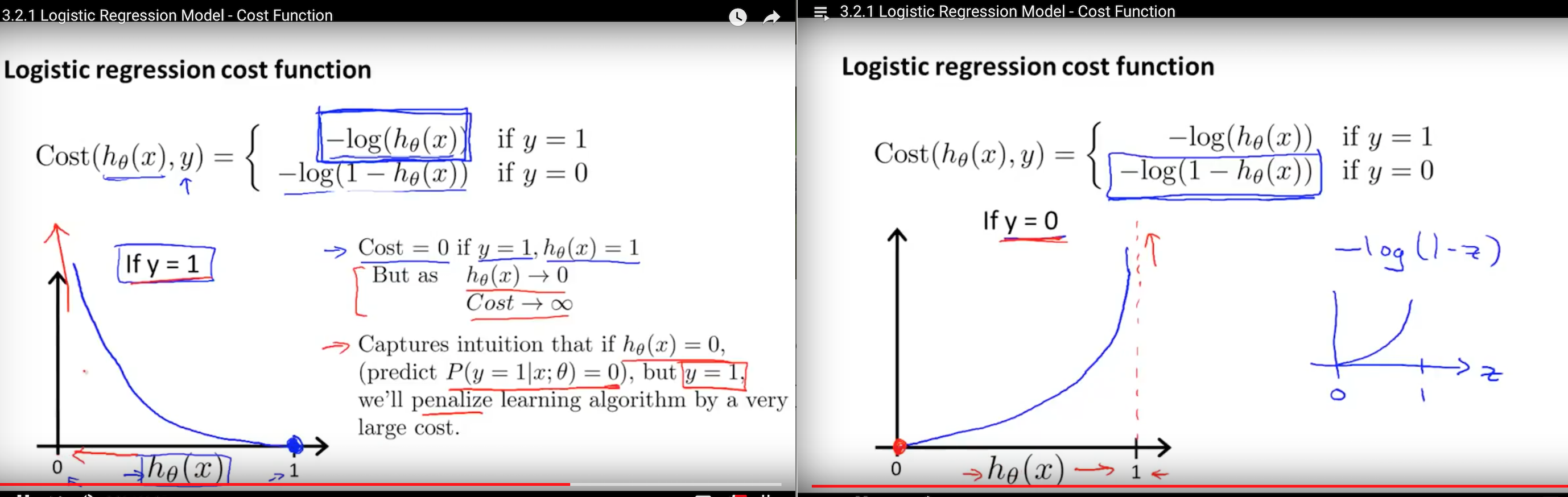
(这两个图是从吴恩达课程中截取出来的)可以看出,二次代价函数存在很多局部最小点,而交叉熵就不会。
附录:
simoid函数的导数:
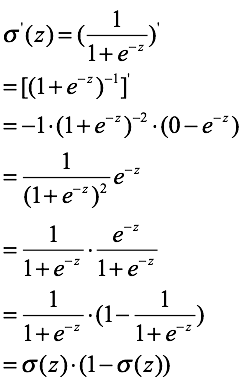
参考:




